ZOJ 3805--解题报告
题目相关:
3805相关链接: http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5337
在二维的矩形上, 机器通过管道(pipe)连接(I型, L型),最终成为一个系统.
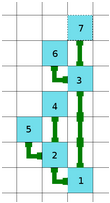
其规则大致提炼如下:
1). 编号大的输出可以成为编号小的输入(隐含拓扑序), 编号1只有输入/没有输出.
2). 每个节点最多有两个输入(弱化的图, 可以用二叉树来模拟)
3). 矩形世界没有高度限制, 但有宽度限制
目标就是:
最能满足要求的最小宽度是多少?
思路解析:
本题隐含拓扑序(有向图), 同时每个节点最多两个子节点, 因此我们采用二叉树去模拟. 这种最优化问题, 有可能是动态规划(树形DP), 通过观察和琢磨. 可得出如下结论:
如果节点i存在子节点j, k, 若节点j的宽度==节点k的宽度, 则取子节点宽度+1, 若子节点不相同, 则取子节点最大宽度的.
转化为公式如下:
1 2 3 | { node(j) + 1; if node(j) == node(k) --(1)node(i) = { { max(node(j), node(k)); if node(j) != node(k) --(2) |
其二叉树的是偏向树, 构建的时候, 往一个方向倾斜就是了.
AC代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 | #include <cstdio>#include <vector>#include <stack>#include <functional>struct tree_node_t { int left_index; int right_index; int value; tree_node_t(int li = -1, int ri = -1, int v = -1) : left_index(li), right_index(ri), value(v) { }};class machine {public: machine() { } // *) 输入数据并构建二叉树 void init_and_buildtree(int n, const std::vector<int> &datas) { arr_tree.resize(n); for ( int i = 1; i < datas.size(); i++ ) { int idx = datas[i] - 1; if ( arr_tree[idx].left_index == -1 ) { arr_tree[idx].left_index = i; } else { arr_tree[idx].right_index = i; } } } // *) 计算结果 // *) 这边采用模拟堆栈的方式, 来实现递归调用, 因为节点有10000个. // *)最差情况会导致二叉树成链表, 导致递归的调用栈达到10000 int calculator() { std::stack<int> frames; frames.push(0); while ( !frames.empty() ) { int idx = frames.top(); const int &li = arr_tree[idx].left_index; const int &ri = arr_tree[idx].right_index; if ( li != -1 && arr_tree[li].value == -1 ) { frames.push(li); } else if ( ri != -1 && arr_tree[ri].value == -1 ) { frames.push(ri); } else { if ( li == -1 ) { arr_tree[idx].value = 1; } else if ( li != -1 && ri == -1 ) { arr_tree[idx].value = arr_tree[li].value; } else if ( li != -1 && ri != -1 ) { if ( arr_tree[li].value == arr_tree[ri].value ) { arr_tree[idx].value = arr_tree[li].value + 1; } else { arr_tree[idx].value = std::max(arr_tree[li].value, arr_tree[ri].value); } } frames.pop(); } } return arr_tree[0].value; }public: std::vector<tree_node_t> arr_tree;};int main(){ int n; while ( scanf("%d", &n) != EOF ) { std::vector<int> datas(n, 0); for ( int i = 1; i < n; i++ ) { scanf("%d", &datas[i]); } machine instance; instance.init_and_buildtree(n, datas); printf("%d\n", instance.calculator()); } return 0;} |
评注: 这边采用堆栈的方式来模拟递归调用, 是因为担心堆栈太深, 不过实际测试数据集, 没那么变态, 用递归的方式实现, 不仅优雅而且编码效率更高.
递归代码片段:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | // *) 递归函数, 划分子问题int evaluate(int idx) { int li = arr_tree[idx].left_index; int ri = arr_tree[idx].right_index; if ( li != -1 ) { evaluate(li); } if ( ri != -1 ) { evaluate(ri); } if ( li == -1 ) { return arr_tree[idx].value = 1; } else if ( li != -1 && ri == -1 ) { return arr_tree[idx].value = arr_tree[li].value; } else { if ( arr_tree[li].value == arr_tree[ri].value ) { arr_tree[idx].value = arr_tree[li].value + 1; } else { arr_tree[idx].value = std::max(arr_tree[li].value, arr_tree[ri].value); } } return arr_tree[idx].value;} // *) 驱动函数int calculator() { return evaluate(0);} |
posted on 2014-09-03 09:45 mumuxinfei 阅读(301) 评论(0) 编辑 收藏 举报





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构