HGAME 2024 WEEK1 Crypto Misc

CRYPTO(已解决3/4)

ezRSA

题目描述：一个简单的RSA

from Crypto.Util.number import *
from secret import flag
m=bytes_to_long(flag)
p=getPrime(1024)
q=getPrime(1024)
n=p*q
phi=(p-1)*(q-1)
e=0x10001
c=pow(m,e,n)
leak1=pow(p,q,n)
leak2=pow(q,p,n)

print(f'leak1={leak1}')
print(f'leak2={leak2}')
print(f'c={c}')

"""
leak1=149127170073611271968182576751290331559018441805725310426095412837589227670757540743929865853650399839102838431507200744724939659463200158012469676979987696419050900842798225665861812331113632892438742724202916416060266581590169063867688299288985734104127632232175657352697898383441323477450658179727728908669
leak2=116122992714670915381309916967490436489020001172880644167179915467021794892927977272080596641785569119134259037522388335198043152206150259103485574558816424740204736215551933482583941959994625356581201054534529395781744338631021423703171146456663432955843598548122593308782245220792018716508538497402576709461
c=10529481867532520034258056773864074017027019578041866245400647840230251661652999709715919620810933437191661180003295923273655675729588558899592524235622728816065501918076120812236580344991140980991532347991252705288633014913479970610056845543523591324177567061948922552275235486615514913932125436543991642607028689762693617305246716492783116813070355512606971626645594961850567586340389705821314842096465631886812281289843132258131809773797777049358789182212570606252509790830994263132020094153646296793522975632191912463919898988349282284972919932761952603379733234575351624039162440021940592552768579639977713099971
"""

我的解答：

根据题目关系式我们可以写出：

leak1 = p^q mod q

leak2 = q^p mod p

根据费马小定理：

a^p−1 ≡ 1 mod p

推出：

leak1 = p
leak2 = q

exp:

import gmpy2
from Crypto.Util.number import *
p=149127170073611271968182576751290331559018441805725310426095412837589227670757540743929865853650399839102838431507200744724939659463200158012469676979987696419050900842798225665861812331113632892438742724202916416060266581590169063867688299288985734104127632232175657352697898383441323477450658179727728908669
q=116122992714670915381309916967490436489020001172880644167179915467021794892927977272080596641785569119134259037522388335198043152206150259103485574558816424740204736215551933482583941959994625356581201054534529395781744338631021423703171146456663432955843598548122593308782245220792018716508538497402576709461
c= 10529481867532520034258056773864074017027019578041866245400647840230251661652999709715919620810933437191661180003295923273655675729588558899592524235622728816065501918076120812236580344991140980991532347991252705288633014913479970610056845543523591324177567061948922552275235486615514913932125436543991642607028689762693617305246716492783116813070355512606971626645594961850567586340389705821314842096465631886812281289843132258131809773797777049358789182212570606252509790830994263132020094153646296793522975632191912463919898988349282284972919932761952603379733234575351624039162440021940592552768579639977713099971

e = 65537
n = p*q
phi = (p-1) * (q-1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#hgame{F3rmat_l1tt1e_the0rem_is_th3_bas1s}

ezMath

题目描述：一个简单的数学题

from Crypto.Util.number import *
from Crypto.Cipher import AES
import random,string
from secret import flag,y,x
def pad(x):
    return x+b'\x00'*(16-len(x)%16)
def encrypt(KEY):
    cipher= AES.new(KEY,AES.MODE_ECB)
    encrypted =cipher.encrypt(flag)
    return encrypted
D = 114514
assert x**2 - D * y**2 == 1
flag=pad(flag)
key=pad(long_to_bytes(y))[:16]
enc=encrypt(key)
print(f'enc={enc}')
#enc=b"\xce\xf1\x94\x84\xe9m\x88\x04\xcb\x9ad\x9e\x08b\xbf\x8b\xd3\r\xe2\x81\x17g\x9c\xd7\x10\x19\x1a\xa6\xc3\x9d\xde\xe7\xe0h\xed/\x00\x95tz)1\\\t8:\xb1,U\xfe\xdec\xf2h\xab`\xe5'\x93\xf8\xde\xb2\x9a\x9a"

我的解答：

考点：佩尔方程

解方程得到y，然后AES即可。

exp:

# sage
from Crypto.Util.number import *
from Crypto.Cipher import AES

a = 1
b = 114514
enc=b"\xce\xf1\x94\x84\xe9m\x88\x04\xcb\x9ad\x9e\x08b\xbf\x8b\xd3\r\xe2\x81\x17g\x9c\xd7\x10\x19\x1a\xa6\xc3\x9d\xde\xe7\xe0h\xed/\x00\x95tz)1\\\t8:\xb1,U\xfe\xdec\xf2h\xab`\xe5'\x93\xf8\xde\xb2\x9a\x9a"

numTry = 1500
def solve_pell(N, numTry):
    cf = continued_fraction(sqrt(N))
    for i in range(numTry):
        denom = cf.denominator(i)
        numer = cf.numerator(i)
        if numer^2 - N * denom^2 == 1:
            return numer, denom
    return None, None

def pad(x):
    return x+b'\x00'*(16-len(x)%16)

N = b//a
x,y = solve_pell(N,numTry)
print(y)
key = pad(long_to_bytes(y))[:16]
cipher = AES.new(key,AES.MODE_ECB)
flag = cipher.decrypt(enc)
print(flag)

# hgame{G0od!_Yo3_k1ow_C0ntinued_Fra3ti0ns!!!!!!!}

 ezPRNG

题目描述：一个简单的随机数

from Crypto.Util.number import *
import uuid
def PRNG(R,mask):
    nextR = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    nextbit=0
    while i!=0:
        nextbit^=(i%2)
        i=i//2
    nextR^=nextbit 
    return (nextR,nextbit)

R=str(uuid.uuid4())
flag='hgame{'+R+'}'
print(flag)
R=R.replace('-','')
Rlist=[int(R[i*8:i*8+8],16) for i in range(4)]

mask=0b10001001000010000100010010001001
output=[]
for i in range(4):
    R=Rlist[i]
    out=''
    for _ in range(1000):
        (R,nextbit)=PRNG(R,mask)
        out+=str(nextbit)
    output.append(out)

print(f'output={output}')
#output=['1111110110111011110000101011010001000111111001111110100101000011110111111100010000111110110111100001001000101101011110111100010010100000011111101101110101011010111000000011110000100011101111011011000100101100110100101110001010001101101110000010001000111100101010010110110111101110011011001011111011010101011000011011000111011011111001101010111100101100110001011010010101110011101001100111000011110111000001101110000001111100000100000101111100010110111001110011010000011011110110011000001101011111111010110011010111010101001000010011110110011110110101011110111010011010010110111111010011101000110101111101111000110011111110010110000100100100101101010101110010101001101010101011110111010011101110000100101111010110101111110001111111110010000000001110011100100001011111110100111011000101001101001110010010001100011000001101000111010010000101101111101011000000101000001110001011001010010001000011000000100010010010010111010011111111011100100100100101111111001110000111110110001111001111100101001001100010', '0010000000001010111100001100011101111101111000100100111010101110010110011001011110101100011101010000001100000110000000011000000110101111111011100100110111011010000100011111000111001000101001110010110010001000110010101011110011101000011111101101011000011110001101011111000110111000011000110011100100101100111100000100100101111001011101110001011011111111011010100010111011000010010101110110100000110100000100010101000010111101001000011000000000111010010101010111101101011111011001000101000100011001100101010110110001010010001010110111011011111101011100111001101111111111010011101111010010011110011111110100110011111110110001000111100010111000101111000011011011111101110101110100111000011100001010110111100011001011010011010111000110101100110100011101101011101000111011000100110110001100110101010110010011011110000111110100111101110000100010000111100010111000010000010001111110110100001000110110100100110110010110111010011111101011110000011101010100110101011110000110101110111011010110110000010000110001', '1110110110010001011100111110111110111001111101010011001111100100001000111001101011010100010111110101110101111010111100101100010011001001011101000101011000110111000010000101001000100111010110001010000111110110111000011001100010001101000010001111111100000101111000100101000000001001001001101110000100111001110001001011010111111010111101101101001110111010111110110011001000010001010100010010110110101011100000101111100100110011110001001001111100101111001111011011010111001001111010001100110001100001100000110000011111010100101111000000101011111010000111110000101111100010000010010111010110100101010101001111100101011100011001001011000101010101001101100010110000010001110011110011100111000110101010111010011010000001100001011000011101101000000011111000101111101011110011000011011000100100110111010011001111101100101100011000101001110101111001000010110010111101110110010101101000000101001011000000001110001110000100000001001111100011010011000000011011101111101001111110001011101100000010001001010011000001', '0001101010101010100001001001100010000101010100001010001000100011101100110001001100001001110000110100010101111010110111001101011011101110000011001000100100101000011011101000111001001010011100010001010110111011100100111110111001010010111010100000100111110101110010010110100001000010010001101111001110100010001011101100111011101011101100100101011010101000101001000101110011011111110110011111111100000000011100000010011000110001000110101010001011000010101000110000101001110101010111011010010111011001010011100010101001100110000110101100010000100110101110100001101001011011110011100110011001010110100101010111110110111100000111010001111101110000000000111011011101000011001010010111001110111000100111011110100101000100011011101100011111000101110110110111111001111000000011100011000010000101001011001101110101000010101001000100110010000101001111100101000001011011010011110001101000001101111010100101001100010100000111000011110101010100011011001110001011110111010111011010101101100000110000001010010101111011']

我的解答：

题目参考：2018-CISCN-oldStreamgame

#对mask提取出相与有效位1
mask = '10001001000010000100010010001001'
for i in range(len(mask)):
    if int(mask[i]) == 1: 
        print(i, end=' ')
#0 4 7 12 17 21 24 28 31

#恢复R
output=['1111110110111011110000101011010001000111111001111110100101000011110111111100010000111110110111100001001000101101011110111100010010100000011111101101110101011010111000000011110000100011101111011011000100101100110100101110001010001101101110000010001000111100101010010110110111101110011011001011111011010101011000011011000111011011111001101010111100101100110001011010010101110011101001100111000011110111000001101110000001111100000100000101111100010110111001110011010000011011110110011000001101011111111010110011010111010101001000010011110110011110110101011110111010011010010110111111010011101000110101111101111000110011111110010110000100100100101101010101110010101001101010101011110111010011101110000100101111010110101111110001111111110010000000001110011100100001011111110100111011000101001101001110010010001100011000001101000111010010000101101111101011000000101000001110001011001010010001000011000000100010010010010111010011111111011100100100100101111111001110000111110110001111001111100101001001100010', '0010000000001010111100001100011101111101111000100100111010101110010110011001011110101100011101010000001100000110000000011000000110101111111011100100110111011010000100011111000111001000101001110010110010001000110010101011110011101000011111101101011000011110001101011111000110111000011000110011100100101100111100000100100101111001011101110001011011111111011010100010111011000010010101110110100000110100000100010101000010111101001000011000000000111010010101010111101101011111011001000101000100011001100101010110110001010010001010110111011011111101011100111001101111111111010011101111010010011110011111110100110011111110110001000111100010111000101111000011011011111101110101110100111000011100001010110111100011001011010011010111000110101100110100011101101011101000111011000100110110001100110101010110010011011110000111110100111101110000100010000111100010111000010000010001111110110100001000110110100100110110010110111010011111101011110000011101010100110101011110000110101110111011010110110000010000110001', '1110110110010001011100111110111110111001111101010011001111100100001000111001101011010100010111110101110101111010111100101100010011001001011101000101011000110111000010000101001000100111010110001010000111110110111000011001100010001101000010001111111100000101111000100101000000001001001001101110000100111001110001001011010111111010111101101101001110111010111110110011001000010001010100010010110110101011100000101111100100110011110001001001111100101111001111011011010111001001111010001100110001100001100000110000011111010100101111000000101011111010000111110000101111100010000010010111010110100101010101001111100101011100011001001011000101010101001101100010110000010001110011110011100111000110101010111010011010000001100001011000011101101000000011111000101111101011110011000011011000100100110111010011001111101100101100011000101001110101111001000010110010111101110110010101101000000101001011000000001110001110000100000001001111100011010011000000011011101111101001111110001011101100000010001001010011000001', '0001101010101010100001001001100010000101010100001010001000100011101100110001001100001001110000110100010101111010110111001101011011101110000011001000100100101000011011101000111001001010011100010001010110111011100100111110111001010010111010100000100111110101110010010110100001000010010001101111001110100010001011101100111011101011101100100101011010101000101001000101110011011111110110011111111100000000011100000010011000110001000110101010001011000010101000110000101001110101010111011010010111011001010011100010101001100110000110101100010000100110101110100001101001011011110011100110011001010110100101010111110110111100000111010001111101110000000000111011011101000011001010010111001110111000100111011110100101000100011011101100011111000101110110110111111001111000000011100011000010000101001011001101110101000010101001000100110010000101001111100101000001011011010011110001101000001101111010100101001100010100000111000011110101010100011011001110001011110111010111011010101101100000110000001010010101111011']
flag = ''
for i in range(4):
    nextbits = output[i]

    R = []
    for _ in range(32):   #每次恢复1bit 一共是32bit 因为与0xffffffff 起到限制位数的作用 
        temp = '0' + ''.join(R) + nextbits[:(32-1-len(R))]   #补全32位 第一个为猜测位0 第二个为已知R位 第三个为nextbit填充位
        print(temp)
        #进行猜测校验判断
        if(int(temp[0]) ^ int(temp[4]) ^ int(temp[7]) ^ int(temp[12]) ^ int(temp[17]) ^ int(temp[21]) ^ int(temp[24]) ^ int(temp[28]) ^ int(temp[31]) == int(nextbits[32-1-len(R)])):
            #猜测成功则填充0
            R.insert(0, '0')  #在第0位插入0
        else:
            R.insert(0, '1')
    R = ''.join(R)
    R = hex(int(R,2))[2:]  #进制转换
    flag += R
print(flag)
#fbbbee823f434f919337907880e4191a
#hgame{fbbbee82-3f43-4f91-9337-907880e4191a}

最后结果根据UUID固定格式来写

MISC(全)

SignIn

换个方式签个到
flag格式：'hgame\{[A-Z_]+\}'

我的解答：

提示说换个视角，看着像拉伸过的图片。试着还原回去看看

放到Word里面编辑

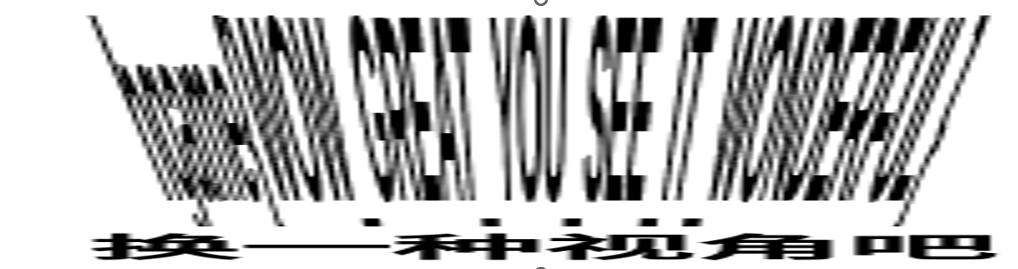
hgame{WOW_GREAT_YOU_SEE_IT_WONDERFUL}

来自星尘的问候

一个即将发售的游戏的主角薇^3带来了一条消息。这段消息隐藏在加密的图片里
但即使解开了图片的六位弱加密,看到的也是一张迷惑的图片。
也许游戏的官网上有这种文字的记录?
补充：flag格式为`hgame\{[a-z0-9_]+\}`

我的解答：

steghide隐写，密码是123456

得到一个压缩包，解压里面有一张图片

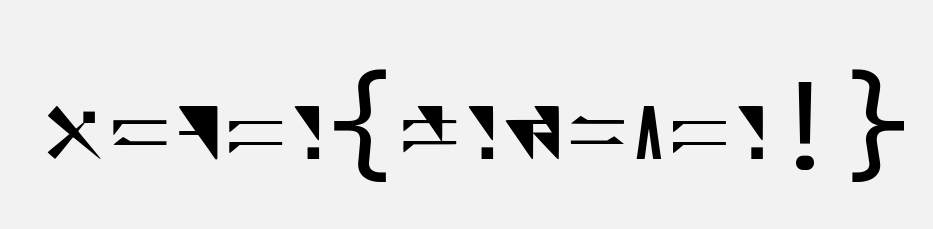
根据题目提示可知该图中的文字为游戏中的字体，然后搜索发现是来自星尘的异星字体，对照表：https://my1l.github.io/Ctrl/CtrlAstr.html

hgame{welc0me!}

simple_attack

怎么解开这个压缩包呢？

我的解答：

附件里面有一张图片和一个压缩包，发现此压缩包中的图片与压缩包外的图片是一致的，一眼丁真，明文攻击

将图片进行压缩(使用bandzip进行压缩)然后与压缩包一起放入爆破工具进行明文攻击即可

得到

data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB/4AAAEhCAYAAAB2sgicAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFiUAABYlAUlSJPAAAH/eSURBVHhe7d0J3E1V+//xpUmjRlNFE6moEEmDBpFQaJ7nedA8apQGlVKkedDwqIwVInMKkaFEpZlmKg9JeUr//3e1Tj/d3fc5e52zz9l7n/N5v15e2Ye4nfvstde6rmtdq9KSJUv+NAAAAAAAAAAAAAAAIJFWc/8FAAAAAAAAAAAAAAAJROIfAAAAAAAAAAAAAIAEI/EPAAAAAAAAAAAAAECCkfgHAAAAAAAAAAAAACDBSPwDAAAAAAAAAAAAAJBgJP4BAAAAAAAAAAAAAEgwEv8AAAAAAAAAAAAAACQYiX8AAAAAAAAAAAAAABKMxD8AAAAAAAAAAAAAAAlG4h8AAAAAAAAAAAAAgAQj8Q8AAAAAAAAAAAAAQIKR+AcAAAAAAAAAAAAAIMFI/AMAAAAAAAAAAAAAkGAk/gEAAAAAAAAAAAAASDAS/wAAAAAAAAAAAAAAJBiJfwAAAAAAAAAAAAAAEozEPwAAAAAAAAAAAAAACUbiHwAAAAAAAAAAAACABCPxDwAAAAAAAAAAAABAgpH4BwAAAAAAAAAAAAAgwUj8AwAAAAAAAAAAAACQYCT+AQAAAAAAAAAAAABIMBL/AAAAAAAAAAAAAAAkGIl/AAAAAAAAAAAAAAASjMQ/AAAAAAAAAAAAAAAJRuIfAAAAAAAAAAAAAIAEI/EPAAAAAAAAAAAAAECCkfgHAAAAAAAAAAAAACDBSPwDAAAAAAAAAAAAAJBgJP4BAAAAAAAAAAAAAEgwEv8AAAAAAAAAAAAAACQYiX8AAAAAAAAAAAAAABKMxD8AAAAAAAAAAAAAAAlG4h8AAAAAAAAAAAAAgAQj8Q8AAAAAAAAAAAAAQIKR+AcAAAAAAAAAAAAAIMFI/AMAAAAAAAAAAAAAkGAk/gEAAAAAAAAAAAAASDAS/wAAAAAAAAAAAAAAJBiJfwAAAAAAAAAAAAAAEozEPwAAAAAAAAAAAAAACUbiHwAAAAAAAAAAAACABCPxDwAAAAAAAAAAAABAgpH4BwAAAAAAAAAAAAAgwUj8AwAAAAAAAAAAAACQYCT+AQAAAAAAAAAAAABIMBL/AAAAAAAAAAAAAAAkGIl/AAAAAAAAAAAAAAASjMQ/AAAAAAAAAAAAAAAJRuIfAAAAAAAAAAAAAIAEI/EPAAAAAAAAAAAAAECCkfgHAAAAAAAAAAAAACDBSPwDAAAAAAAAAAAAAJBgJP4BAAAAAAAAAAAAAEgwEv8AAAAAAAAAAAAAACQYiX8AAAAAAAAAAAAAABKMxD8AAAAAAAAAAAAAAAlG4h8AAAAAAAAAAAAAgAQj8Q8AAAAAAAAAAAAAQIKR+AcAAAAAAAAAAAAAIMFI/AMAAAAAAAAAAAAAkGAk/gEAAAAAAAAAAAAASDAS/wAAAAAAAAAAAAAAJBiJfwAAAAAAAAAAAAAAEozEPwAAAAAAAAAAAAAACUbiHwAAAAAAAAAAAACABCPxDwAAAAAAAAAAAABAgpH4BwAAAAAAAAAAAAAgwUj8AwAAAAAAAAAAAACQYCT+AQAAAAAAAAAAAABIMBL/AAAAAAAAAAAAAAAkGIl/AAAAAAAAAAAAAAASjMQ/AAAAAAAAAAAAAAAJRuIfAAAAAAAAAAAAAIAEI/EPAAAAAAAAAAAAAECCkfgHAAAAAAAAAAAAACDBSPwDAAAAAAAAAAAAAJBgJP4BAAAAAAAAAAAAAEgwEv8AAAAAAAAAAAAAACQYiX8AAAAAAAAAAAAAABKMxD8AAAAAAAAAAAAAAAlG4h8AAAAAAAAAAAAAgAQj8Q8AAAAAAAAAAAAAQIKR+AcAAAAAAAAAAAAAIMFI/AMAAAAAAAAAAAAAkGAk/gEAAAAAAAAAAAAASDAS/wAAAAAAAAAAAAAAJBiJfwAAAAAAAAAAAAAAEozEPwAAAAAAAAAAAAAACUbiHwAAAAAAAAAAAACABCPxDwAAAAAAAAAAAABAgpH4BwAAAAAAAAAAAAAgwUj8AwAAAAAAAAAAAACQYCT+AQAAAAAAAAAAAABIMBL/AAAAAAAAAAAAAAAkGIl/AAAAAAAAAAAAAAASjMQ/AAAAAAAAAAAAAAAJRuIfAAAAAAAAAAAAAIAEI/EPAAAAAAAAAAAAAECCkfgHAAAAAAAAAAAAACDBSPwDAAAAAAAAAAAAAJBgJP4BAAAAAAAAAAAAAEgwEv8AAAAAAAAAAAAAACQYiX8AAAAAAAAAAAAAABKMxD8AAAAAAAAAAAAAAAlG4h8AAAAAAAAAAAAAgAQj8Q8AAAAAAAAAAAAAQIKR+AcAAAAAAAAAAAAAIMFI/AMAAAAAAAAAAAAAkGAk/gEAAAAAAAAAAAAASDAS/wAAAAAAAAAAAAAAJBiJfwAAAAAAAAAAAAAAEozEPwAAAAAAAAAAAAAACUbiHwAAAAAAAAAAAACABKu0ZMmSP93PAQAAAAAAAABAjCxfvtzMmzfPzJo1y/6YP3++/e/ChQvd7zCmatWqpmHDhqZ69er2v40aNTL169c36667rvsdAACg2JH4BwAAAAAAAAAgRn7//Xczc+ZM8+yzz5pBgwaZ//73v+5Xgttwww3N9ddfb8466yz3CgAAKGYl0+pfVZFXX321qVKlSqAfPXv2dP8nAAAAACTDTz/9ZI499thy1zjl/VAQGQAA5E7P1PKeteX90LNaz2ygPL/99psZNmyYadeunWnZsqV58skns0r6i/6/X375xV0BAIBixxn/AAAAAAAAAABE7L333rO781UcMnnyZPcqAABAMCT+AQAAAAAAAACIiNr69+/f33To0MEMHjzYvQoA0VFnGnUcOfLII02tWrVsxxp1Irn//vvNggULzJ9/coo4EEck/gEAAAAAAAAAiIBa8d99993m9NNPNwsXLnSvAkA0Vq5caY8badu2rbnooovMyJEj/z5uZOLEiea6664ze+65p+nVq5c9YhtAvJD4BwAAKHJffvmlDSJxrigAAAAAxIeS/rfeequ57bbb3CsAEB3t4n/ppZfMOeecY+bMmeNe/TcVAqgA4I477rDjGID4IPEPAABQpLRgmzp1qjnxxBNt20gAAAAAQDwoWaaW2do1CwBx8O6775quXbv+vcM/k3vvvdcMGTKEtv9AjJD4BwAAllp5ffPNN2bcuHGmT58+5rzzzjOHH3642W677ewO8WnTprnfiST47bffzIsvvmh39k+fPt29CgAAAACImpJk/fr1Y6c/gNhQHGngwIHmk08+ca8Eo9jTV1995a4QNcVvFcdVPFdxXcV3FedVvFdxX8V/UdxI/AMAUMJ+//13M2vWLHPzzTeb3XbbzdSrV8906NDBXH311ebZZ581o0aN4ozBBPruu+9Mly5dzJlnnsn3DwAAAABiZsqUKaZ3797uKjtK6rRp08aew60frVq1MlWrVnW/CgB+FD+aMWOGuwpu7NixZu7cue4KcaHvp+K6iu8qzqt4r+K+iv8qDqx4sOLCKD4k/gEAKEGq4h02bJhp166dadGihenRo4d3RS/iR1W7Y8aMMR07djSPPPKIexUAAAAAEBc//PCDeeyxx7Jag3fq1MkMGDDAzJ8/38ycOdPutH3++eftD+3U/fjjj83nn39uf49+LwAEpd3gr7/+urvyM2/ePPczxJ2ePYoDKx6sjgCKIypOjOJB4h8AgBLz3nvvmbPOOsu2gJ88ebJ7FUm3aNEic/3119vgzpw5c9yrAAAAAIC4UIv/kSNHmv79+7tXgmnevLkZOnSoefLJJ03r1q3NRhtt5H7lnypVqmQ22WQT+3v0eydOnGhq1qzpfhUA8oOd48mk9v+KIypOrHgxigOJfwAASoQm4QouqLXT4MGD3atIOlXl6vt5yCGHmF69erlXAQAAAABx8/3335shQ4a4q2C0hn/88cft7szVVgseztfv3XXXXc3RRx/tXgGA/FhjjTXcz5BEiiueeOKJtsBM3USRbCT+AQAoAUr6q5XgpZdeypnvRUI7Rd59911blXvyySezyx8AAAAAYk67K0eMGOGuMttrr73MDTfcYLbcckv3CgDkx2abbWaaNWvmrvxsv/327mdIKh0BcO6555qnn36aDg4JR+IfAIAipwTxK6+8Ym699Vbz3//+172KJPvuu+/MHXfcYdq1a0f3BgAAAABIgGXLlplJkya5q8w23HBDc9VVV5m6deu6VwAgfzbffHN7rIivNm3a2O4iSD7FjXWMqOLIiicjmUj8AwBQ5KZMmWK6du1K0r8ILF261DzyyCNmzz33NLfffjvfUwAAAABIiC+++MK89dZb7iqz448/PuvdtwDgq3LlyqZ9+/Zmu+22c68Eo+NEqlWr5q6QdIo1Ko48bdo09wqShsQ/AABFTG39H374YduuCcn1yy+/mKeeesq0bt3aXH755RzXAAAA/mXFihVm6tSpf+/SSSLNecaPH286d+5spk+f7l4FgOIwY8YM8/7777ur9LTbXx3e1llnHfcKAORf06ZN7fEiGoOCuPbaa83BBx9sKlWq5F5BMVAcWUfGsuEomUj8AwBQpNSSadSoUWbQoEHuleAaNWpkunfvbiZOnGgWLFhgFi9ebCf/KCzt8FfCv2XLljYAzjn+AABgVUqUq230ZZddZnbccUdz4IEHmvvuu8/873//c78j/jTPfO2118xpp51m6tWrZw499FA7/1m5cqX7HQCQfCrO8inIb9Gihdlpp53cFQAUhhL4HTp0MA899JCpX7++e/XfVBhw9913m4suusisu+667lXEgeK3Sth/9dVXNq6r+K7ivL6ef/55M2bMGHeFJCHxDwBAkfr+++/NkCFD3FUwmtT37dvXBl/PPfdce0aXJvOrrcaUoZB0hn+vXr1ssIeEPwAAWFXZRLnOVX300UcT0xFIxama6wwYMMAceeSRpnbt2uaII46w1+wqAlCsVNTts65r0KCB2WijjdwVABSOYoDqODJ8+HBbUHrQQQf93QFgn332Md26dbOFp2eeeSZdSWJKBRwbbLCBjesqvqu1g+K96Yo5yvPyyy/TdTSBiOIDAFCk1B51xIgR7iozVfT279/fdOrUyZ7rhcLSrja1fbzuuutMkyZNTJcuXTiiAQAAWL/99ptt33/yyScnNlH+888/m//85z+mY8eOpm7durZwYeTIke5XAaC4qWjLJ3mi5Mzqq6/urgCg8DbeeGNz6qmn2lihuoEuWbLEDBs2zG5QqVWrFu39E0RxXsV79b1U/DcodZGdO3euu0JSkPgHAKAILV++3Lz++uvuKrO99trLnuG15ZZbuldQKNr5MXjwYDsBb9asmbn//vvZ7QYAAP5BLf2VNNecIam0y1+dCcaNG+deAYDS8eOPP9ri/CC0s5a1OQAgbHq29OjRwxx++OHulczGjx9vj6tBcpD4BwCgCH399dfmrbfeclfpadKn3eXaeYXCUPBeE+fzzz/fntuo3XsEwQEAAACgOH3zzTfuZ5nVqVPn77baAACEqVq1auass84y2223nXslvXfeeccWryE5SPwDAFCE1CI+6G4CtYpt2rSpu0I+aXf/lVdeac/jPfTQQ80zzzwT2u7+c845xxYSAAAAAADi5ffff3c/y6xq1aqc7w8AyJvGjRubww47zF2lN23aNDN//nx3hSQg8Q8AQBGaN2+e+1l62kXQqlUrzvQvEAV7dC5amK389T3s1q2bufnmm0316tXdqwAAAACAuFi5cqX7WWY623+11QjbAwDyQ3Hg9u3bBzpWRjHMoHFmxAMzCAAAisyvv/4auI1gixYtbKt5JNNuu+1m+vXrZy688EKzzjrruFcBAAAAAHHy5Zdfup8BABC9bbbZxjRv3txdpadNTH/88Ye7QtyR+AcAoMgo8R+0BVODBg1oIZhA2uV/zTXXmP79+5u9997bVKpUyf0KAAAAAAAAAFRMscWgm8G063/FihXuCnFH4h8AgCKjCszffvvNXaVXt25d20YQyaFq3Oeee85cddVVZrPNNnOvAgAAAAAAAEBm2kSkXf9BfPHFF3ajGZKBxD8AAEVm8eLFZuHChe4qvSBnOSEe6tevb/r27Wtefvlle0QDZz4CAAAAAAAAyEatWrXcz1BMiBgDAFCi1NJprbXWcleIq6pVq5o777zTDB8+3HTq1MlUrlzZ/QoAAAAAAAAA+NPxr40aNXJXFfv222/Njz/+6K4QdyT+AQAoUXXq1LHJf8RTKuH/9ttvm3POOcdsvPHG7lcAAAAAAAAAIHvqJkpH0eLDdxQAACBGVGnbu3dvM2vWLBL+AAAAAAAAAIBASPwDAADEgNr4DxkyxIwYMcKcdNJJZoMNNnC/AgAAAAAAAABAeiT+AQAAIlK/fn3TrVs3M2fOHPPUU0+ZAw44wKyzzjruVwEAAAAAAAAACIbEPwAAQAFtvvnmpnv37mbatGlm4sSJpnPnzqZWrVqmUqVK7ncAAAAAAAAAAOCHxD8AAECB6Lz+Hj16mHPPPdfUq1fPrLHGGu5XAAAAAAAAAADIXqUlS5b86X5e1JYvX25uvvlm06dPH/dKel27djUXX3yxu/L3559/mp9++sl88MEH5r333jOzZs0y3333nf3vwoUL3e/6yz777GPP8d15553NTjvtZBo0aGC22mors9Zaa7nfUbz0ffnyyy/te/TRRx+Z2bNnm///mTQzZsww//3vf93v+ovep0022cS+T3Xr1rX/3XrrrUs+aaLPmt6zzz77zP744osvzLvvvmt++eUX+3O1jy5LraX1GatZs6bZYYcdzPbbb28TUNWqVSv593PFihX2fXv77bfNp59+aj+TZd/HDTfc0DRu3Nhsu+22pmHDhvbHjjvuGMk9+/vvv5tvvvnG3kP6WvXjxx9/tLuIV7XddtvZ+2aLLbaw44w+A/reKwlZ7LuMVx2P9X2cO3eufc/Kuz9S79Nmm21mx+LUvaF7JUn3xieffGLOOOMMM336dPdK+XbbbTfz2GOP2X933Ol58fHHH9sfqXFOz4nynqupe1Qt8/Ws0Nime1T3bLGPcz179jQ33HCDu0qvXbt2dl6kcaBUpcYHfZ40Nmgs/eqrr/41D9GYWadOHft50pi/66672s9SFOPn0qVL/54z6fOvr1fXuu9XVXbeVErzy0zKey5U9D6m5kwaJ1PPBP03zs9P/dvOO+88M2zYMPdKejpm5LDDDnNX8VaKz3RUTPP2b7/91q6B5s2bZz7//HN7D2vOUN56MjU/qFKlih0b1W1Hnw3ND9Zbbz33u+KrGO7toHPUlDFjxpimTZu6q+RatmyZXVsq9qG57Pvvv2/XbJrDqgNUWauOX5rDag6i51GNGjVK8jmeev9WXQcEiXdoHpR6//RDXbfyfa8PGjTInHLKKe4qPebipaeU12qp+G9qTZ9pHKxatapdd6277rp/P7N1P2+zzTb2OU63vP+zePFiG8N866237PynbIxEz1GNf3o/FQPSD+UhAJSv2OMFZQWdnycphgwS/xXKJvGvQUGTmKFDh5qXX37ZvPnmm+5X/Cko0apVK3PCCSeYPfbYw050ioHeo6+//tou4F955RUzcuRI9yvZ0USwY8eO5vDDDzeNGjUqiXORV65cad9DTYwnTJhgf5R96GRLA3fLli1tgKhU3k/R+KAJshbpCqSVTSIGkfosHnvssTaguNpq+WuoomS/klMvvfSSGTJkSE7f/7322sscddRRpn379vbfUCxS79GoUaPs97W8gJAPvTdaeB966KGmWbNmsV8kFcOkLfU91Bg3YsSInJ6pq9LztUWLFmb//fe3iVH924spAUTiP7Ow5mup8VNjf77fQz2XdC+88MILOc2dUs+qY445xj7nSyn5qfmTgowaT/r165fzc0EBtA4dOpg2bdrYZEI+n/u+ii3xX+rPdPwfJfr0/Z80aZIZN26cGTt2rPuV3B1wwAHmkEMOsfe0guNxDNSR+E8GzTO+//57884779hntz6nuY5bKRq/tF4/4ogjTPPmzYt2/NK9rsSVntka+8N6/0SfJ93nBx54oA3Wh11IQeIf6ZTSWi31zB4/fry9l8tL7mdL965i5rqXU8UBpUbPGiUjH3nkETvulC12TEdziRtvvLFkYr5AEKUULyiLxH9xIvFfAZ/EvwYGVdY9/PDDpn///u7V8OhmUkvgI488MrETPr3/WrQ/+uijNkiTDwpgn3766XYRnGnSpwmnFsxBxGFQ02dswYIFZvjw4eb55583M2fOdL+SP/r3nnbaaTapUb16dfdqNPL1/dJC5MUXX7T3bpjBhE6dOpnzzz/fNGnSJNQHe+o+6tWrl5k8ebJ7NRxKhup7ffbZZ9vdJUmtnlZAVMUQCnTm6z5RwE1FWbo/ateuHcv3KqmTtlRCduDAgaZv3745FbUEpaCBCnZ032655ZaJ3zlQDMGkfM3ZUsER/bnPPPOMezV3GhOuuOIKc/TRR4f6XurrnT9/vp076X7wCeYEoXnTBRdcYD8HUQbL8jlHl99++8288cYb5v7778/bHFSFRGeeeaadq8QhgFYsiX+e6RDN16dOnWrX2SrWCnssLI/mBLqnVYCfzwIpnwRhlNKNuz7zjijle5xLJftHjx5t15f5et6sqtjGL80HVIxfyHs99R6qIFI79MJYuych8a9x9dZbb7VxBV8qfL3jjjts96tS5zvfikKhE7wq1tScTXFLzeGy2VTjS/dxXAub87XO0c7jO++80zz55JPuFT8k/v+Pb0Fi0mRbQJnvNboP4gX5R+K/OMW31CQBtLhTizHduKoWzkfSX3TzXX755aZt27Zm8ODBdkBKCg3OSuBoB8Vxxx2X1wWwJpcKYGsQ1QRTE86k0/un4IGCT2ptddVVVxUk6S/63HXp0sXsueeetoJUi8Nioc+GPiP6rHTu3DnUpL/oPtWYcP3115tFixa5V7Onwo/XX3/dLmZ0H4Wd9BcFVpRc0nuiBcTPP//sfiUZtOh+6KGHbLHFRRddlNf7RIvXe++91+y99952bFZRDnKj56nuQ43hSsQrgFyIpL/o773uuuvs36vPEIqTgiNa/Gl3XJhJf9GYcOWVV9p5mhbWGrNzpWeHgqoaZ7QAzUfwW+OkCiY1x1ABq+7DYpJ6dmpXt/6N+ZyD6s/W81nPaf2dYXwGShnPdGg80vfi9ttvt2sg3ccauwuRCBTN5TWma4zUer/YxkeER+tKJasVLFXxtDZsFCLpL6uOX5ozhLHujIKOMHr66aftjrhC3+up91DdX8466yx7dEyxyyXpr4D/LbfcQtIf/6LPlWLiiifph2JLur8KQX9PKpalbrBajyUpbu5Dawz9+7ThLdukP4C/EC9AsSPxnyUlZFXhooEhXwn/spScOPnkk20y9rvvvnOvxpOCIwoia0A79dRTQ0+spqO/66STTjJXX3117N+niqQmzVr8amdCoYIH5dEkWoFQ7SRQm9Wk02dCnw19RvL9udRi+vjjj7dnbGVLARwVEKgVfz4S/mUpyKJAgIJXOrso7rSgSwVnlXgr1OJSUsUS++23n91FVKyLy3xLJTg13oWdkPXF97D4aEGlXTiFCI7omaIdXj169Mi6WC4VzFG7aSW8ChH41rNF81m9P8VyD6jQ45JLLinYszNFf5f+Tv3d+hrgh2c6tIbUWf1ae6j4WONgIT8HZenzqB25+mxo/Q+kaIzQ81pJJrWbLlRMqDwav3SvqEOkdqwlpVBFcyUdYdS6dWtb/FuoDQ4VUdFxtvO3pFChip5x2ST9tbvvtttus0V5QIrGQm2qOfjgg22xXNT3sWKnWteokKfYCvf0Xuv+1XqzkDF2oBgRL0ApIPGfBbUh1sLksssuiyQQod3X2v3y2WefuVfiRYul++67z062Cjl4lqX3Sd0YNNlLirhNmlelYwZOPPFEe0ZhUifPqQ4d+mwUiu4BfS/1/vm+b/p6VXCRzcI8V/p6VRwxZcoU90r8aJKkxIAKoqJc+Og5oM4RavWd1GKjKKQSsoVMcKK0KEnTu3dvc8455xRsjNDnWDuhVGD2ww8/uFeDSX29UQRz9HWrI4ICukkOeus5q4Bf1Ltg9Hfra9DXUkwBx3zimQ7t8FfCP7VTMC7zAn0d+rrUElfdKFDaUrvDdERavneH+VJ7Vh1fpWR6nLsf6rmoTSJ6/7Q2J4FVGPpMKA6iOaovJf3VYlmdswDRfax4lRLsihvFKXYpqcK9JHazLI9ixZobab1G3ARBqUvLJpts4q4gxAtQSkj8e/rwww/tWThRVnSLknJK/n/88cfulXhQUcSFF15o2zTHYTIyfvx4+z5pYRlncZ80p6gKXotznbmXpAeTvlbtflAwWZ+JQtP7pvsi6PsW9deboiCMqhDjlvzX+6OzXnUeY5QTtbJUfZ20YqOoRJGQRWlRgEcJeB3jEMV8ROPBNddcY8/7DSLqrzdF7W67d++eyOS/Atp9+/YtSEefIPQ16GuJewImajzTofFGySh1W4hTwr8sHT+hY9eCjusoPipOSe0Oi1PCf1W6f1S4pO6UcXz2xGWTSKnRs/aVV16xxda+lPTXRoQ99tjDvYJSp7W8ntdKrCvBHlcaD1PdLJPcvVRj+eOPP26uvfZa9wqQ2YYbbmiLmbfddlv3CogXoNSQ+Pfwzjvv2Oq6KBNxq9LXoUlMXIIPen8UIIu6KKIsVb5r8Rvn5P+vv/5q/vOf/8R60pyinVA33XRTrHeCl6WvVYn3Qp0ZXp6g75sW5QokRf31pmgicvPNN8em7b922agrhnaz6N6Om6QUG0UpLglOFC8FlRXYVHFJlJ5//nkb3M6URNcO0q5du0b+9aYo+a+kZ5IWn9oFo6ScghtxGlfinoCJGs90iOaa2lEfRSc9X0HHdRSngQMHxqpAqSKpZJcSvVpbxkXcNomUCn0G9KzNZo6kpL+OsNprr71MpUqV3KsoZeqGpCI4PbeTch9r45xi1UncWZtL0Q5KmzaS6ThNxu6/EC9AKSLxH5CSXmqJ9eabb7pX4kGLz4cfftgOYFFSQExFEXF7f1IUTNQ56Uk4szwJlJBWkiIJ76cS7Zdeemkskuip9+3TTz91r/ybvl4dIxKHrzdF97UquqMOcmoS9PTTT9uJWpyDw4w3FYtLQhbFS58x7ViP4oiU8ujr0Lj1xx9/uFf+SV/v3XffbRehcaJ7NCkFfno2xHkXjBbzSsAMGDCAxfwqeKYjqTSuJ604CqVHzx6tO+PyLFe8SMcGxm2TSCnQZ0CfBd9ER9WqVe3Ghf3335/EESx1wFUCXc/ApFGRoXb+J617qbr8qitSnBKViL8OHTrYQrt11lnHvVLaiBegVJH4D0A76nXmqW9SW9Wxqq5q27btP37ss88+7neEQ5OAKLsQKBCmgFiYO3W0yGjVqtW/3jv9qF+/vvtdfuKSvCyEdO9fWJ+/JLyf33zzjbnrrrsCt/Cp6H0L857V+/bEE0/Y9mhl6V7Sotw36V/RWNO0aVP3O3KnpNSrr74a2SJJkx9VQGqsCWPRk+/xWd9nFXCoJSj+ou+hggRhJGTVtkxBqLLfv9SPbJ8TSLbUjibtWA9K42TZz4/GBo0RYVGBZnlzpFzuCY1VZb9uPb/0HAuDduXp6477Gee57oLRWFH2fdSPsD8Dem6pkn/YsGHuldLGMx35VN64rh9h3tdJKo5CPKWby+p1/XqutKbUuexRPsv1nNYRdkoWhhkvkoqe4foR5jo4yXScgo4q9Y0v6POnwtRDDz2UpD+sfHXAreiZrR9h38cqNNWmoKQk/xVrVcxV81AgKM11Ne5Xr17dvVLaiBeglFVasmRJsvrcZElJNrWr1sInCCXfNKnRg1ZVN0GCsgq2qlWlBoCdd97ZbLDBBu5X/k0BLyUl1WpIu/ZzPSPusMMOswnOsAK+QakoQm2e9G/IhQZS/Rt0tuP2229vqlSpknaBoe/nF198Yd83Tdp8JkJKCOj7c+CBB7pX0tttt91scDLMAb0s38/nqvTeHXDAAWbfffe1P9dnYK211nK/Wr4VK1bYXed6/9SycubMme5X/GhBqPfmoIMOcq/kx7Rp00zLli3dVXqp71fNmjUD3bvNmzc3xx9/vH0PN998c7PaauXXQ4V5z+p9e+aZZ+znPeWHH34wV155ZeBdEAoIadeEgtrVqlWr8H7R91r3yuuvv26rB3NZNOjrfeCBB0ytWrXcK4WhVsA6BkNjcrYJAt2/HTt2tOPzDjvskHZ81t+nAJkCukoi5nIEh6psu3TpYtZdd133SmEouKOK9kwBtkKMbykvvfSSueCCC7L6HuqeUeBJ54E2btzYbLzxxhmDUPo+6u/67LPPzIwZM+w9q/sg3d+fevYnWc+ePW0L1SB0LqOeO3o/4yTbOVuQ4KY+SzpL/JBDDjENGzZMe28uXbrUzJ4927aH7NevX067kk899VTTrVu3f4w9PveEnu36ujWO6Vlf0XNeC1sdHaBzybXA1RiWy9etOdNpp52W16Bvtt9v8Q1oa76i772e/VtuuWXGXRDLli0z8+bNM6NGjbKfAd/AeVlqlXv//febunXrulfyQ58BvS9BAwcqQNE8vBB4pqMsn3n+qjSet2jRws6JlRzQGabrr79+2vEqNUZqXqDPgtaR2X4OjznmGLv+1teRrUGDBplTTjnFXcVXuvmRz7wjSmGMc9n+WzVmaa2uH5p765me6fkT5tqzEM/yimSbeC4rtRZQDEfvYY0aNTLGPDT+//jjj/Y5rnFmxIgRadfCYa2LfO7rfM7FtalAXXV81/96rzVX0XM2is9MkvjOt6Kgr+/GG2/MaefvBx98YC655JKcE9C6tw4++GAbV2rQoIGNY62xxhruV8unsVBxZ53Rr6IDbUbJdTzR16H7TuuBfMtlnTNy5Egb08l2npJOGJ+LYqHPU5DYWVLceeedtthu9dVXd69kJ5fPbtiIF+Rf0PugkDFk5I7EfwU0SOhMR+3M1QQnHQVgzz77bHP44YenDTxVRAsStT5TQi2XYJR2/isAUSg+RREVOfLII81ZZ51lB45ME76K6P3TJFA705RMzWSXXXYx7du3t10cgijEoOb7+WzUqJE56aST7AMpXbI6CP3dSmqoojvozvhVFaLoxDfxr6pYJWvSnd2jh7ja/Oih6vvZC+OeXTVYqMWM7l8dJ5JJrl+3Jj3apZTt4lSfE00iCxUEUIA22zMJRe+XAvX6/GSzqNHfr52vffv2tWNMNl+DuiWoKKyQgZO4TdpUaHT++ed7Bws0rqjqVc/XMMYYPbdmzZplA6jlJUTzuVgplFJN/B933HFpCxE11mrBp8B3NtXvCuy98MILdtzOJpGuv1/3WqpQLmgwNteve9GiReY///mPPZM6m69bzxqNfbVr13avhC/bhXzQ91Bjh8ZDFU5o8Z7tWKxjtSZNmmSf17kEeMNIFmYS18Q/z3SUx2eer/tGn9Wjjz46Y/FWJvo8zJ8/39xzzz1Zn9ue672joL7P3/2///3PzmOCjucqiAhj/tS6dWv7HCqP4iWvvfaau8pMY74KL4LefypyzibGUpYK8HItVveZY2lurfN1leTSz7ONdYjWinrWKX6htZyvqIK0YST9VdijJLoS/rl+DnTPK4Go2Ifu3bKbH8J6n+KQ+M8l6a85yhFHHJHTZ7ZUaBxTYa9PRyBtyvDpSKln3Zprrule8afPteZOa6+9tnvFT7afpVWpeF/joeZxuSaa9QzR2KKYXy7z8UIl17Jd5yxevNh2m8q0MUifEY0jKoxSrHujjTb6R1GU/n4Vs+vIgFULoDQ2k/j/i+5JPV+zWRfkm894Ieecc449oiWMIuVsP7v5kO3XQrwgOBL/xYnEfwU0SKQWGRUtVFLBWCXBNttsM/dq9jRAqDrolltuySo4qzYjSsIXop2LzqrVREs7lLOhCk8lL3ffffecktarUlJTbeRUjJDNgrgihRjUgn4+tcNbn0kl/sNeiGk3lN47LYJ9qWuAdl3li2/i/5prrrE7Gyp6uOvXtfjRrqBc6J597rnn7ITZd5Ko8UPJGAWzpk6daouH0gVF9Pu1M1TJ01y/biU/NRHp0aOH99ddyHFGNMnVe6Pdqz40cVMSUBO3MCa9ChSpmEQLAgWLfGgBpgSDisQKJU6TNgUr9VnT+OJDhWEKrm611VbulXBpAayFrwphUoG/fC5WCqUUE//692pcrGhOos+5zv1XAiTXZJ0Wj2pP7jsOyOmnn27vA30N+q+CTekoOKbfp68/l69b45fGUH3d2bTnzHdhaTZzdBWN6r3JVHyqRM/ll18eaqcaPfv1/dduimwKJiXfuy/jmvjnmY7yBJnn6/3Wmls7cPR5CJPWkPocaIz0TVBqrqI5jgLthRDXe9tH0DlqypgxY0Jv95ytIHMsza30WQ0jwVXWzz//bJ972bSrLXTxdq7JQr1/mtftvffepnLlyu7V8Gh9ok4wKuRP3U9hrYuiTvyrU4Ribb5dORVvUCxSz1qS/vmTpLVarh1elfBXa311XA0r7psSRvxXz3DN5zfddFP3SviyTVhqXpJu/aW5kDZIqBDS5/Oh900b5xSDVOdTEv/xpRi91rHqEhhE2MUs2X5284F4Qf7FKYaM8IT75C0i2p2oRUBFi38FH7SQ1iQojKS/aEGjKkgl1LO5gZTACLqAzpX+HgW9fGkxoQFYieI99tgj1Mmf/qwWLVrYPzvbgoS4UsJfk1klqBT4yMdCTIlcBUCVXPalljZKJseBPpuqUC8vyKDPnxIYmiDnmjwX3bOaJOhe8L1nlXDX+6bFlB6a6QKNmtRrAhfW162gub7P2VQQFnKc0XujIJVvgkCFRQq4KLgVRoJANNlSsP/BBx+0VbQ+9PWrqEuT1VKkz/Yrr7ziroLRe6zvfb6S/qJdQ1rs6zOt3XYkcZJL84qKnvsdOnSw3YBUaBjGokkLac0PgwZ0V6WdnR9++KE9ckI7jtNRoEfzzCZNmuT8dev/33XXXe1CWe+HLz2rtOskTvQ1Pf300+7q33Q/qyOPFsxhH0+jZ78CmZpvagzJxrPPPmuTIqWEZzqyoXtZc2AlfxX8CjvpL1pDKrmiwKDvfF473VVEAugzpBbUKgrXEXL5SKZoHagkmtbsvkaPHm3H4ULQ36OvMZukfypepGe4CoLykfQXxVNUVKDvl75v+v4VA7332ST9RZsjSPojRcUxmutm81nSs1pxbcXetAYJO+kvqfivxgqNGb5xLdFuenV00781ThRb1VqnIlp/jB071s5hfYtC9L5pDqwEH0n/+NI6Q/PSoEl/ff6VdC90e/g4I14AkPivkIKtukHLoyoqtXnUQiTsCYwCUeo0oArQbCYuqlpWZVE+KWGZKVFZnlTyUpXfYQXuyqOJj1qm6+/K5j2ME1W6Dx061D7w9VAKI2mRjoIJmiyorbYPJTPi/kDSZ0GfCVXEhrmY1fdELRyzuWcnTpxoF0QVjTWiP1OBcp2xF+Z4o/dABRJa4PtS0irfAe9sF5pKlqkQQwvMfNwvGl/UOksdI3woafHOO++4q9KhXZUTJkzwSvRo/FHFbaF2NmjBq79TwXuNuSge+r5qJ6batYVJu0Kuu+4672elWoyr04sWcem6rejPVdvQmjVrulfCofdBzyrNY33o3tC5dXGhc461W6qi91AdiLTIz8c8fVUqTNLz2TdxLCqgU6Ax33P2uOCZDl+a/2qOqsJBFVrlc+0o+nxpbPSdz2scUvB9xYoV7hWUGq3RVcyn+JE+Q/l87oiCySqC8R23VOhaiHFL4/2AAQOyShbqvdTzW0du5vueT9H3S983ff90xGe+v3/5pI4Qmh9l897fcccddnckSX+kqOBOG0V86X7SZ/Coo47KW+HOqjRWaMzQOJzNBjrF43T8TJyoUFwx1vJobqQj3PK5QQLRUgxNz+xMGwVWpU1iQbvklgLiBcBfkjurjYgmMUoeKgCVLwo8qI1hNgk5tUpUO5h80QNIrdDSJSrLowmYktdhJy8rogWLzsDXQO+bjI0Dfc2pSndVsRZyAVqtWjVz7rnnek2alcyI+24X3U+6r/IROE7ds5ps+dCDXO2nK6LPgcYb3Tf5+Lp1n6gQwrcC8a233jJff/21u8oPFTGpwMpHvpJlZWlxqcS02nYHpXtEk7a4dMYoFLXT13MpKI07Kj7SOFRo6gDQrFkzd4Wk03xNO57y9VnSn6vnilqd+VASM13lvsYxPRfy9XVrF4AWnr6JLY3JmgPGgRbyFXWe0funqv1C7XZQ4liJwmy6JSl5/MEHH7ir4sYzHT7U5UGFzyrkDquzXhCaa+tIK3Xg86Fk6o8//uiuUEqUfFdxinZ1FSLBlaJxS2OW5jo+9OzUkY35pPFeXQp96b5X8l2bYPKx7s1E3z+dkb3NNtu4V5JFzyMdAZHNe6/uDPo8kfRHio6L0G79dIXK5VEyTR3GGjZsWND7WH+XOq3o7/ZN/mtDmzp/KG4RB1pvaYOQ5pplqVhVsZIwuoAivubOnet1LKvWTCqWZgz/P8QLgL+Q+PegCYRu1kIMDtkm5NROLZ+DgiYfvkl/BZf1vmlXdCEnf0qWq6VtNgUUUVISQRWyhax0L6tx48Zpz5Mqj86JimvbUwVltFsonxMh/dm6X1u1auVeyZ2q7rV4yud9o52rOkrCJwmkCZRvxw8fmuCq+rK8xU5F8p0sK0uTN52x6hNwS7X5LiX6Hvrs9lcBzQ477OCugOwUar6mP1/tx8NSqMIXBcZ8z3xWcV9cAmIV0ZxPZ9PmO1FcVrbdkvQc1W6OuLUXDRvPdPjQuk2dUfLV5SETdQE69thjbRvcoFTgOH/+fHeFUqDntT6neuYUsjhlVUpQaw3nQ+v1fB7dow0oKnD0Ge9F613tYK1Xr557BT60G/CJJ56wG218qUhWHSQKWbiCeFNxkOKR6VrNl0fFOyrYjLJ4Rt37skn+K7k2adIkdxWt8ePH2w1gZSmmqeJt2vMXN9+j0QoVPygWxAtQakj8B5RKXutc+kLJJiEnCs7mY1eW/ky1e9VExEc+d1pnomSsEr6+rfCioq9VhRVhnUWcLb1vrVu39mqPrEDCDz/84K7iQ0FcVbAXoohCk4fjjz/eXeVGExIl/guxCFdFtr7fPvK5Y0Rt5XwKjFQso3Gm0JNd36SfgmD6t+V7p41o51lFFa6FpH/z+++/764y01mbBJ6Qq7PPPts+R/NNz2kVe/km0Sui4wN8kk3ZUneLgw46yF0Fo+CDbyC/kPSs1zw97GMdgtLzR7vGfb9/2imaz0K6OOCZjiBSidSrrroq8p1sderUsQVSQam4haMfSoeS1C+++KJp3759pG3hNQfRvNmnYGnmzJl5e5YrVqROHUHPI07R168gfFJ32kdNyYDHH3/cJvB96WiDfB/DieTRRjLfzV66j7VDWc/PqClmrzWBb3czFTsE3WGdT+XtVFayMMqNYSiMbI7KKVT8oBgQL0ApIvEfkFpyRJG8ziYhp4laPnZlaZHou5DTrnElQvO50zoTTY70/QtzJ3Y+qDpVbdaqV6/uXomWKu59EgMKeKk6MW5UPFPIQIImE2oTmgstUlSsUKjPwkYbbeR9f3z66adm2bJl7io82inis9DUe6WARSE6sZRHZ0L5dMdQJfnChQvdVfHzGRMaNWpE0A8501imwqnVV1/dvZJfVatWzXnMl1NPPdXO9wo1z1Ry1efrVgFPXBP/eg6oUC7qYONOO+1kd437UEGFz3EoScMzHUGsvfbadpdwu3btIk2kpqgAUc8Sn6TB559/bn799Vd3hWK17bbb2p3pUY1RZW2xxRZeZ/rqOf7FF1+4q3Bpbfjss8+6q2BU8FOIDk3FauXKlTY+pxb/vrQxRoVWJBKxKnWP0O53n459elZqJ3pc7mOtpRTH1NGvPl599VWvf3ehaJzUOocd3cVPBcU+47nG8UJ3Vk4q4gWZrbfeerYLXiY6WkjPCiQDif8A1LLouOOOiyR5nU1CTucxLVmyxF2FR8cI+Oz21wTl/PPP9wqa5It2YuuhGIevpTxq16RERZzOatIi0OfsYlXHxi0poF2Yun8KORHShPzAAw90V9lRAkiFIIXUtGlTr++3Apz56PCgcUatjILSOaxKXkU12dWY0rFjR3eV2ejRowuyoPzpp5/cz9LTxE4TvHxZtGiR+1lmCvbHIeCPZFOxYaFbt+25555eO+7KUtW5Ov5oJ36h6FmlnYI+5s2b534WL1E/B1L09ytx6XtUknb25LP1cpR4piOInXfeOfJuZ2UpgaG5cVBq9U/iv/jpDPi4FOmLihx9PqeSj2Mp1PlESTOfbmMabwvdUbOYqMOCkv5qHey7S1mbYtRZh6Q/ylKMR0cZ+dDnSfPfONFnW0dY+MYzdbxB3BJaWlf4jvNIno8++sj07Nkz8HiuPJUKbhjHgyFekJkKn4N0X9WGkHxsAkR+EGEPQDdkVK1AxDchl4+d1xpgfM940o7lBg0auKvoNWvWLLQ27KVCgTifz37czrfUg127MQtJD3Lds9mOGSqYUSuvQrc7r1Gjhv1+B6XOIkGTy0FpnBk2bJi7ykwtknQOa9TnnPnunM3nMQkpQZ8BQSd3QBLoPswlAZ8tJQFyCchoHFP1dyHpWaUztH2osDRuiS2NvyqWi8t5l0pk6BnuU2g6efLkvO3AjBLPdCTZJpts4jVGfvvtt6HPi4EgtHZs0aKFu8osH8/yr776ymu8l7gE4ZNISX8V1nXt2tU76a9E0RVXXBGrDSeIB32uJkyY4FXQGOUmuUzUoeWEE05wV8GMHTvWFj/EheakRxxxRCzfX4RHO6gfffRRO64Hoee+irdq1arlXkE6xAuCUTFp0LnBggUL3M8QdyT+M9BiRO3TolyQbL755jZpHVQ+dl5/9tlndqAJSgOrWs4UqtVuEBrktYsnyiKOpFEyY4cddnBXmWkH+IoVK9xVtJT80S7MKNSuXTvrohcdKeLznodFu759Ev/5GGdmz55tXnvtNXeVme7nKN6rsnx3zr733nt5rdbUPRj0DKitttrKttgFioG6rUTRBlHFM9merac5ic4JjqIAxzdZEMcdrUoUK7AXJ5qz+xzTpWfp1KlT3VXx4JmOJFtrrbXsGBmUEp/56LgHZKLuXT7PQRUHh7leV7JQG0SCJiwkbkH4pJkyZYrtZul75q82NOl84SCtfFF6NDaok5GPqDfJpaMYftu2bb066KroYebMme4qenFc5yBceob269fPPPTQQ+6VzM4880y6QHggXhCM1j5BY2nKEeqzi/gj8Z9BVEHkVWlB5BN4kDADD7qZJ06c6JXkU+uSrbfe2l3FhxKbubZhLyWqQPP57C1fvjw2u57UNlC72KOgds3169d3V8Hp/dbCJKod2Ntvv737WTA6uzcs+ty89dZbgXctKMmmIok4FBf57pzVYjLsoolVLV26NHBLbnXEiEvi/+OPP/betQKkKOikBVRUhZpqC51N4EtnUNarV89dFZZvskC7WX/++Wd3FT0V+MVxt2A2x3RpzNYcqljwTEcx8DkHVJ+BuBQ/o7Soza8KeYPSczzM9brG+UmTJrmrYLQLl2RWdtR1Tzv9fZP+2l3YrVu3yGObiC91jvU5nikOm+QyUTxQay0fGs/i0MZac+N999031u8vcqdCrt69e7urzFRso07GdIEIhnhBcIoLBz0yU90H1KkC8UfiP40dd9zR7viIwwDhsxNXfM5VzkSLOU0Cg1LgWxPAOO32T9Gu5qh2gSeRKr7U6jIo7XaJy5lYOiNfX38UfHcJpehr9k2+h0lJYI17QYW5IFq4cKFX0OiAAw6IVXGRz85ZBYfz2aZJu3KDVqorWZnPZ5zPgkTPmrlz57orwI8Wddtss427KjzfDjkpKlaI6mw+n8WdaMyP07mXmmtuscUW7ipefI/p0ll56ppULHimoxhUqVLFa16sFupAoWkerzlIUIoThdmlxLe7iwLd2oVLMsufzoC+5JJLvLoriJL+3bt3J+mPCqlwzafDq6hTU9w/UxpnlDz36cymMU3H90RNuQh1EkXx0kaqPn36BC7kUrxDR7X4tIgvdcQL/ATNR8yYMYPC94Qg8Z+GgrE+1dP5tOmmm5pGjRq5q8wUcAurHauCWT6TwCh3rwWhSZ9PEKeUqXjDpwXf77//Hot2L3p4ZpN4D1M25y3pHt9ss83cVeGpyMNnUqQFUVgVhx9++KFXazlN4OJ0Nr3vzlkFbvJxr2gHz5gxYwJNwjQO+uxmy4aOqvGhz4CeX4AvFUiq20pU9Hf77vjXPegTiAqbnvE+zyqdZf7jjz+6q2gp4KHEbByLTMX3mC4V2KrFarHgmY5ioM+kT2GW1kFAFHw/pytXrnRXufHt7iKKFUXVlS/JVFh02223eSf9O3ToYG655RaS/khL83ufzV5avyjmloQCHiXPfY5w0nrHt6NGPmidw3EoxUtx1F69epmXXnrJvZKe1r5nnXVW3uN3xYR4gT/lUYIUI+hYlAkTJrD+TQAS/2koiKwd4nGgZKBPAkWLsLBuQFU8+lTyRLl7LQgF5qMMtCdNEqtMNRnS7vUoqXWPbxJID9goJyW6b1VkVGgaq3wWmjquI27FRXrvfArFVDSRj7OyP//8czNs2DB3lZ7GwWxak/vQDk6fiuRBgwbZc0KZQMKXdttHGXxac801vcfPQtyDmSQ1EKxFfNQFfukoUNegQQN3lZmSJp9++qm7Sjae6SgWKoglQYkkyKbgPAzqHOBzHrbmPbSu9qdA/7XXXmsGDhzoXglGnRV0LEDUc03EnzoGTps2zV1lFrdOTeloTr777ru7q2AUA48yHqG4YJw30yE3+mzpWI2+ffu6VzK74IIL7LFoPD+DI17gT+ueoB3HR44cGYvuKEiPxH8aUbbcLkvtWH0m7GGd26aWTz7VjlHvXgvC971E8miXVtRFO+uvv75X20XdO1F/Ln0TV2GNMzqTXouroHT2rs8RFIWgCbhPkkDFVGEnCbSDZ8CAAbZKPQjtsFQb23xSwZpaWPm466677FlnQFBxGD91xItv2704PKu0s9lHWON+rrRIVoFdnGkd4fOZUIetYih64pkOAKVBY59P4j9JycK4+Pnnn03Pnj29k/777befPdM/ymOwkBwq2PTp3NGwYcNYdWrKRAXiWi8GFfX51Uq8UXhYvHS8ZY8ePQLfczqu5dRTT+Vcf0/EC/z5HI+tDVuDBw+m41nMkfivgFpu+7YozicFoHzOKw8rAKXg3Zw5c9xVZnHYvZaJ3sc4fW8RPu16iLqdjyYYPl0HFGD2KRTIB9/EVVjjjM4p0k71oLQQ8hkPC8Unia7KyDBbZmvy98orr5jevXu7V9LT+WBBJ3S5UDJHSR0fKja79NJL7fnQxZAEQ/7piJI4JA595z9169aN/FmlxZ1PIOzrr792P4tW/fr1Y9u2L0VzTZ/xr1h2jfNMB4DS4NsZMmnJwqgp8Xj77bcHXt+laJ2npBItoRGE5p4+8zatG5RITxLNyX029mlX7U8//eSuCk/3bpy76CJ76uBy991321bpQWjHulr8c1yLP+IF2dEcQsWDQTz66KN20xZx2/gi8V8B3XxRnrVdlnapR9G6XEGs7777zl1lpglglGfsBhVFO/M40yCtIg+1+NI5LRq8L7nkEnsm3EUXXeR+V3LkexdzEKuttprXJEOJ/6gn9/p6ozhHTGOMzocMQom1uLZr8tk5q3+zdnCEQed0DhkyxFx++eWBq4aPOOKIgrQFVTJHu3t8d0Kr4OzEE0+07c9+++039ypQPiWvNU+KmsZ9H3EolPQ9wzoO9L757MaOiuYiNWvWdFeZFcuucZ7pSBp1uFPByqxZs+zOlTvvvNPOQdQmO+jxSUAhLFu2zHz11Ve2OFZz5C5dutidgMccc4z7HYXj2xlSrat9i4FLmdY/TzzxhD0D2ocC9vfee68tLgWC0Ljy0UcfuavMkrDZqyytdXwKYZT417wgKuqMQkv34pPq0OnTweWKK64we+yxh7tCUMQLsqf3Lui8UvPACy+80IwbN47kf0yR+K+Akuxx3H1SaNrZ5dO+TQuMJExQSjHxn0rua1JfNrmvc/y1Y1KtcHRu0GWXXWYef/xxO3j7tPyKC58HZ1zoaIC4VyPmi89OEbXGLob7V/9mBcxypT/nlltuMSeffLJZuHChezU9BQgLeT6YdnO2bt3aXQWnf0/nzp1thbMqoplIoiJ6fiVtB5kWVFEUWhWDpDwHtI7w2Z2xaNEie15y0vFMRxzp+6NdVjrDeNXkfvPmzW2xv9ph6yxQzafUHvull17y6noHhEVJOBXjv/HGG/9I7qtISmtc7bZt06aNDbQqKaxWq0HXAGHSbvSPP/7YXWWmpFsUG1mSSMkhxWJ0rr8PJf3vuOOOxO3GRrR8N3vF4agyX5qT+xSaal4X1ZxcGyaSVliBYMaMGWO7uASl53zHjh0pAskC8YLs6fN20EEHmSOPPNK9kp6S/1o/af6hrw/xQuK/AqoI9N25lW9RnOfis4hM0gSlWNsmaeevEvVK7o8ePdo8/PDDNrnfrl07+/1RckTV9sWQ3C82+v7Eodio0Is4JXN1TlFQCnjFoaNDGLJpH6dAkMZl3d/nn3++DVirlWNQCggpiFTIVmE69uKoo47y3vWfogD93nvvbS644AJbAKBxDkg6He2igq+oqWAiacE77cSOw3uXiW+3Lo3vSR/feKYjSsuXL/87ud+vXz+b3D/hhBPsEX5K7ivx2LJlS5L7iFSqGH/VTntK7qsYX924NC6qGF8dJ6JO7qej3bA+hV5J6QwZNc0DNDb5JIdELY1vvPFGuirAm5JIvpu9krhhxbfbYVRjruYq2cZNEF+K0ffs2TNw7F1xu1NOOaVocxf5RrwgNyqauPrqq+3nMAh9rjVvadasmbnuuuvM+PHj7RiqrxfRIvFfAe3CittkJopz6X0Xcz5tMZEbBbd0rp4CW6nkvhJsmtAquX/YYYfZtkBK7k+cONH9X8VPwT29D8hOoasi1abIZ1H1wgsv2AIjJQri9kPBZB++bYFVSdmqVStbra77+5lnnvEq2kkFhKJo/ZjaRZcL/XtVANCpUyczdOhQOwYCosVSHFr9J5GS/kkLxCepw4NPQez06dMTf048z3QUggJe33zzjS1eVvFjKrmvgqpUcv/ss8+2yf2XX37Zqx05ECZ1mlCwX0WsqeR+eZ32lNxPWjG+nld6bgWlrhrsWkxPRSFK+l988cVenwWtDe+55x7aQSMrCxYscD8LJqm70RUj9PnafWLhYapRo4bZZJNN3BWKgTrkqMjvzTffdK+kp8KPq666iiNbckC8IHf6/Cl+rDhyUIoD3H///ebQQw+1cxPFr1mHRYvEfwXisvs2SkqqfPvtt+4qM+2kIOGaPwpyzZs3zzz44IO23Y+CW6q+UmCr1JL76ahTR9y6daBiOr9QZ1Uiv/bbbz/bASSqgJCK6dS2X61Kc6XA6HHHHWf23HNPWzWtYAXHAJQ2FWoSTEYcldp8hGc68kU7pNXtSAkxFTjXq1fPJlFvvvlmkvuIDc1HNQY+/fTT5vjjj7dBT31eVfyaxOR+Or7JQt/dtqVGnx19Prp27eqd9O/Tp4/tAgdkw+csex01ouLIJNLuX8VQg1I8/I8//nBXhcOxw8VFnyHNCR566CH3SmbXXHON3fCC0hDneIHixypaURcqJBPZMVTof//7n9ckUFVK7LgLnyqmnnzySbP//vubJk2a2Mq/sWPHul8Fkk1BDtr/5I8Wjnfffbd5/vnnzS677OJejYaOF9AxA0HbRWWiIP8NN9xgK1DVBk3jIl0AgOKnnTAqJkqCJLQYDBPPdIRJnyW17b/ooovMTjvtZLsdPfHEEyT5ETsqTNGufhXnKzGm46leeeWVoknyl8cnTkRHvsymTJliuz/4jG9K+qvrCTv9kYtly5a5n2WmtuNJ2UVblnbRaw0RlMZvdW0ptDgeO4zsTZ061W7ACUrnqh999NGRHPVcTIgXhEcdqrT+UlzZ51gCxANPE1RIlWk+bStVlciOu/Coil5nozRu3NgGvHzO3QKSQm2KfDqLIBgF2O677z7z9ttvm7POOis2Z4OpXZR26asDQZhSwVa6AACIE98jsNS+PMl4piMM6hwxbNgwe4yZ2varALqYE6hIrkWLFtmWpg0bNrS7+rVju1T4JAt1pFBSAvBRmDVrlt3p75v0v/XWW+3mEGJwyJbvEU20oQeC07pOydKgY7s26lx66aUFP34V0UpCvEDxZMWVVaSoOLPizUgGEv+okBZzql4PijN2w6EAwu23324TWAokEOgCkK047rxUe161i9Iu/bCt2gVAu61U+KBjUgAgCdgtj1Km5/Xrr79uz4U89thjzeTJk92vAPGi83ofeeQR06xZM1uo75M4Kwa+yUIl/tdbbz13hVWpyEnHlgQ9+1l0LKnWOwcffDBJf+REhfJRtLOPgjaq+exWVVcTdcEtNOLqxUGdKB944AEzatQo90p6GtfV9UUdroB0oo4XaCxljEoOEv+okHZb+FRyIzeadCtJpfMAlfgn4Q8gW+oQok4hav3YvXt3W1AUJzpfT1+X2lPmq13UM888Yw444ADTqVMnM2bMGPtMAwAA8aMuc3fddZddB5HwR5x99NFH5txzzzWXX355ySX8U0opWRhHWj+p0xlJfyA4tc/36YKoeUkU49zqq6/OvZ1wekaOGDHC9O3b172SmboGtWnThu89YinV4UrxZc2BWaslB4l/IAZUsaVJgRJUUQ6g2iV7xBFH2FZz+nq060ZVigCSSQFJtYFUIF2FRXFqf6+Wn2eccYZt06+zzPJFbVc1th511FF2TKMDAIC4ivsZf0A+fPbZZ3Y+oPlKVIXP2mmlltkXXnihTarpfPaJEyeagw46yP0OlDrNoYcPH27nk5q7RkUt3tUVQ50GdG6wilsHDBjgfjWeVOSrHWIIx6uvvlqyRSeI1lZbbcVOTyCDuXPn2rlk0Dltq1atzPnnn8+ROAik0PGCGTNm2HhyKXa4KgYk/hGa2rVru5/Bh3ahPvTQQ6Zz584FCXY1bdr07+T+Cy+8YBNhCrjpXFYVHTzxxBPm4osvtokynVdIWz4g+XRvn3nmmTZQFKfkvyqadZaZWv8PHTrUBt3zRQUA7du3t++DdmsBQL4tWLDA/SwY3zP+gKT74IMPzHnnnWcTqvmm5KOCq0ru9+rVy/6d7733nj0rU/fqSy+9ZIsPNE/Yd9997dp2jTXWcP83SpmKRgcNGmTOPvtsr3PYs6VifLV/V5BVxfhK7n/88cd2x5W6ej377LPmyiuvtEdiaG0f92eHdtlqty3CMXDgQHPVVVeZ77//3r0CAIgDjcs61//dd991r6SnYj51EKpZs6Z7BaUmrvECxY3Hjh1rTj/9dHb4JxizbyBC2un/+OOPm2uvvda9Eg4FC0444QQbvFJyX2fGzZ8/3yb3FThIJfd1LpyS+5tuuimBLSDmVGGvHT3jx48399xzj3eSXIHKLl26mClTprhX4kPBwBYtWthAlgLx7dq1c78Svv79+9s2ak899RTt/wEAiIiK8C655BKvs60zSe3cV1JMyX21Wn3//fdtcl/zIM0ztD5SS9W9997bJvcpckY6CnyqKERr5zCL9BXsP+yww/7RaU/F+EruK8CqI6uU3FcxvpL71apVY9d8Edprr73MjTfeaMcuHxrLVBhC8h+FxBEfQMUU31e8TuNzUCoo3H333d0VEB+KG1922WXeBa/qlta7d2+7vlOHLMWxER0S/0BEFERQG0md558LLRK1g79Pnz5m+vTp5rvvvrPBAl1rR4uS+zvvvLPZaKONSO4j8VTU0rZt26L44Rto1v2rIp3GjRv/3SJfbWgVEAxKkzZVICsAHkf6NyoQ/9xzz9nq0hNPPNH9SrjUokpdVq644go7ZgJAPnC0SHql/EwvdUpW3XbbbTkn/fUZuuaaa8zLL79sPv30U/PFF1/YJK0KHZXc33PPPc0WW2zB9wdZU+BTyflck/4KhKpwV3N3zcO1c19FqKt22tM8vxiT+1999RXFthVQjEbrHY1jvp5//nnTrVs388MPP7hXgPz68ssvza+//uquksencIFjDeBLm+x84vvnnHOOOemkk8zqq6/uXkEpimO8QDFS5ZR8kv6nnnqqmT17tnnxxRft55o8VDyQ+EdotKMcwfme+1OWAgSqJtSfox382uFft25dzgVCUTv66KNtkKMYfuR6bqx2ye+6667mkUceMT179gy8U2TUqFG2CjnOFfv6tzVp0sRWis6ZM8cGXLUzKmwKuKql74cffuheAYDwKEAa1G677WY22WQTd1UaeKaXJu2IevLJJ712RK1K8wHNC95++21bOKCE2X777Wc222wz2okjVErQq2DWd7dTirpPaJ2u/18dp1S4q7l7qRWi6J6P01FjcbPmmmvagPlNN93kXglOaxnFlH7++Wf3CoDyqGDBZ14O+FAXK8Xkgsb31e1FcSgdhYPSFrd4geLEmrOqkDoIHaWmTtaai6hgSse5Ij5YGQMR+OWXX2xLv6Dn/qxKi0IFurTIa926tdlggw3crwDF79tvvzXLly93V5DKlSvbisq77rorcPJfSQqdFRp3mjTWqlXL7oaaNGmSGTJkiFeHgyB0dIL+fM79BxCmFStWeBV3qhq+1JKWPNNLk3ZQax3kS7v7H330UZvs13N7++23J9GPvFGyWoFPFcz60lx19OjRtjuXOvMpKFrKFESmA0562ryh3Z/q2OhLhdLaZaoYE5BP6txRKt07dE+yExtBaOxNzU+DUMxO47027qG0xTFe8PnnnwcuztZnWQWymuuysz+eWCkjNFrQJaWSO+o211OnTjX9+vVzV8Gosmvo0KHm3nvvtYEuqqhQDFStWKNGDXeFbGmS1aFDB9vWNggVHU2YMCFRu2+0+D7ggANs0VPYXQC0SFPrf7UJBoAwaF7sswNPu5XVDi/JeKYjk6VLl9pkqu+uO511riPS1CWC3VEoBHWDUrtSH5qXqpuFunHpzN5iLUxRHMInIaYjthYvXuyuUBGNbZdffrlNCPnq1auXufXWW0n+w4ta2fsUJv30009m2bJl7ipZNAYtWrTIXWWmhFYxHr2CcGm99/TTT5uHHnrIvZKZjpts166du0Ipi2O8QEeu6hjpIPRZPuSQQ8hPxRiJf1RIC1Wfih0t6JJy3pMq+KOixZhapvhUdensULUJbNGiBTtbUNI4I7JiSoyrI4iKhIJ46623sj5qJEpluwAMGjTItlLNlZL/alFFwAxAGDSW6LzxoLbccsuSO0uUZ3rpmTVrln1uB6XA+/3332+uvvpqG+wCCkGB2FdffdWrO5/m39rxd/jhh9tuXMXMN1mos2JpRR/MxhtvbJP/+hz5UvK/e/furGUQmG8RjzoGJjF+IOowtWTJEneVmeblQCba1Pfwww+7q8w0th9zzDHsjoYVt3iBxkh9poPQMWvqcMVnOd7IIKJCqiLyCbAkKXj3ww8/uJ8VnnYPjBw50l1lpiCCdrZus8027hWgeGjSonOAglKFeVIKjKKw9dZbB64enjx5stckM45U7HDggQfaVqpvvPGGOfHEE92vZEcBsxEjRrgrAMjejz/+aJMdQa2//vqJbynKMx3paJ2otuk+SQPtJDnhhBMIKqGgFNcYM2aMu8pMgdhbbrnFNGnSxL1S/NZbbz33s8zU4cPneVjqqlWrZj9P6ubmS90hVSxF8h9B1a5d2/0sMz2/fXbNx4kSWu+//767yqxKlSruZ0D51ElYbc4/+eQT90p66gqkzSsa4wGJW7xA87WgRa/t27enQCoBSPyjQhpMNKgEpbZPSajkVgV/VJNVtdWeNm2aV3vLM888k7N/ULTUPi3oufSioh21iUX5NG63bNky0ARM41CxnGuvTii77LKLTdzrSJTmzZu7X/H33HPPRX4cDICKJeVc+K+//trMnDnTXWW2+eabJ76lKM90pKPAltZBQbVq1coceeSRJP1RcO+9917gs3pFR23tscce7qo0VK9e3f0smKQXGxea1nI33HCD2Wuvvdwrwd122222WyQddRCE5p8+5s2b536WLD4xWN1/vmMcSouKq3r37m0LWoO67rrrbMwK+Ue8IDvq6hKkQEqf43333ZcW/wlA4h8VWnPNNc2mm27qrjLT2chR7qQPSjuLokrqKLjpE/BS+2q1T4lyMJ0/f777GRA+Jap9OotoUqTJESqmqv1GjRq5q/SU+FcxVLFQAYCORFEHAHVK8UlApWjxNmHCBHcFANnxDYxuv/327mfJxTMd6XzwwQdeyVTtdq1Ro4a7KjztwlHgEKVlxYoVXuv1HXfc0R7LF2WByoIFC9zPCkeJMZ959ueff06HF0/a/HHHHXdklfy/9tpr7RFmUR5xiWRQzDdo7EBUxJOEhNqqFO/w2fCw7bbbesXCUVq0oU9dfHW2f1AXXnihOfjgg0mU4h/iFi9QXi+Ixo0bs9s/IUj8o0JqoewTbFEFZRIqudWZIOhgFjbtdPEZ2LVzIMpKU02QkzapR/L4tAWWpFaZF8oGG2wQeEKooLYCnMVm3XXXNZ07dzYPPvigbanmS+1dfc4ABFA4mmvGPXmguZPPs0oBV98dV3HFMx3lUZB09uzZ7iozJVPVNj3KAKl2y9Iuu/SoUH/OnDnuKrNmzZrZJFGUovic6iz6HXbYwV1lph1kixcvdlcIatddd7U7/7NZz1x99dXmkUceIfmPtDbZZBOvmKPu5SRs+FqVjpbyiQFrTNcYB5Rn7ty5pkePHoGPrtJmvnPOOcfGqFAYxAv86esJWvCs9T6f52Qg8Y+0fCt4tEiO++5R7Sx655133FVh+bZx0fn++Ty/JZMouyOgdGih6TPW6AwtClIqptZPQYNDKtgq1t032v3frl07c9NNN5mqVau6V4PRuVY+7QABFI4WpCpairOFCxfaVtFBqVOL7zgVVzzTUR4lJn0KxNVCMuqdJLqPfc4DRnFQob7PZ3XnnXf2Ou8+bIq9RLHjX7tht956a3eVmboo0EkwO9oMouPMskn+33777eaxxx4j+Y8KafzyOVr09ddfD3ymeVz4bsDSJooox3XE1/fff2/P9Q96DrrmsldeeaWpVauWewWFQLzAnwqev/rqK3eV3jbbbEP3ioQg8Y+0fHftaNCKeyW3kv5BK/PCpoE9KO10iTrgFWV3BJQOJQl8doxonElalXmhVatWzf0sPe1qUgV8sdJkVMn/yy67zL0SjAL9Ot8KQPxMnz499oU5ek75tDTfaaedbLeWYsAzHeVRkaFP23zttos66E43itKkjk8+BR9RH9Piu5M1LHpm+Yz1ir9MmTLFdv+AH61n1O5fO/99jzHT+37rrbeaAQMGkPxHudZee20be/ShQp4kHReoNv8+G7BU0AWUpTFUY+nAgQPdK5ldcMEFtngLhUW8wJ/mZ0HnCRSyJAeJf6SlczrVvi6ouFd/aiE/depUd1V4Pg8eVXJVqVLFXUUjyu4IKB0bbbSR12JT44zaa6FiQVvTKVioys5ipjNXjzvuOHPkkUe6V4Kh6AmIL81N4po80Jiq5IaPqDs8hYlnOsqjwnCfAmitQaO8J9SFImk7GhEOrX+DUpG+xrwo6b6KolhVyWjf5Ngbb7xhd0vCn97vDh06mJ49e2aV/L/iiivMSy+9ZFauXOleBf6PCph8PleKqS5atMhdxZvvvLxFixZZdddA8dNxkOqiEtQxxxxjjj/+eBuPQuERL/Cj2LA2hmWidT4dUZKDxD/S0q5Rn+CdFhUK4MW1+lMBHJ+KqjBpp4tPwEuVXFEOpnpA6kEUVXcElI5sqswVOCr2hHUuNCH0DQoVMwVltfPfh8brYj0GAUi6KLs3ZfL555+bsWPHuqvMtIgvpgAjz3SUR/erT3JSbcSjpOTvW2+95a5QSnwS/+pwsv7667uraOh5qJ1tUdCzS8+woEaMGBHZ11oMdIyZkv/XXHONeyU4jcEXX3yxTf7TdQFlqdNr8+bN3VVmSbqX1eZfHQqCaty4cdEcv4XwqGuECq+Crj/VpUUFV8TkokO8wI/W4kG6weps/8qVK7srxB2Jf6SlxLNv+zpVwQU9F6SQVIygry2qdi9aYCWpHZbOwyHghULRjhGfoy00SdJkCeXTAqNOnTruCqLPWKNGjdxVZhqvCYwB8fTaa6+Z2bNnu6v40JgxYcKEwOc+SsOGDU3NmjXdVXHgmY6y9EyNa/CtPFEmUxGtJLVDV2eKKLsZbr755l7dIWXkyJGBdpShfNo5evrpp5vbbrvNvRKcxuDOnTubIUOGsMbBP6jLzu677+6ugtHnKAnP9UmTJnlt/lJbdpJaWNUvv/xiHn300cCfI8XizjrrLOJxESNeAJD4RwCaAPpUqelhqMlV3GiXiSanCEYPSHVvAArBt8pck6RRo0YlqpgG0VJAQwFKAMmnQKOeAXHbJa4zzJXU8LHPPvvYyvliwjMdSaakpAJyQNzpWCp1TInKOuusY9ti+xg0aFAsY0VJoqTkaaedZi688EL3SnCaP3Xt2tW8+uqrJP/xN3ULVBGPT9xXnyHfVtWFpt3+GnOC0i7tBg0auCvgr8LVp59+2jz00EPulcyU9G/btq09ogXRIV4AkPhHAL7BO+nfv7/55ptv3FX0VLmvpL9PRVUpU0Wj2sAloYIXxUGLTN8dIwMHDmSHIACUqFdeecV88MEH7ip6CqAPHz7cBhiCUoCxSZMm7qp48ExHks2aNcsrURBnxXCeNwVB5dP7osRb1PENJcn0LAtK8YVnn33WJuSQPSUA1PL/ggsucK8Ep+Mvu3TpYsaNG0fyH39Tt6bWrVu7q8zifi/rs62OrzqWIKiWLVuaLbbYwl0BxnbVefjhh91VZocffrg5++yz6RoRE8QLUOpI/COjbNo+aRDTYBaXhYQqUfv27euukkFVYGq3HwVNbgYMGOCugPxTNWzTpk29WgOrBet//vMfzgUGgBKkwPVzzz1nixXjQGc/KgDqo1gDjDzTkav58+e7nxWWdvtrDVQsxc9RHXEXJp8z9wtN41ZU63UFsuPQzVDPMD3LfGiDgYq9knSsQhytv/769tx+JZp8aQ512WWX2W6dJP8hG220kWnVqpW7CibO97Kef88//7y7ykznZ+vfr+4HgGgz4913323HyyD0GdJu/2rVqrlXEDXiBSh1JP6RkSY+Gmh8gnfSu3fvWOyw//77783jjz8eeeBjrbXW8mqdpUBCFF+zKnb1frHbH4VWr149c9BBB7mrYB555BEzfvx4dwWER+O1xm0A8dWvXz/bKi/qoLWCCSow9TkTXPNqza+LNcDIMx2rWm+99cyOO+7orjJTC/Nly5a5q8LQOKLzQJ988kn3SvItXLjQ/Prrr+4qmQqd+NemBx8ffvih+1nhpJ45cYi16Bl2yCGHmF122cW9EozOS542bZq7QraUYNJ5/9km/3VcQNzbtaNwtLN0v/32c1fBxPFeVhHpU0895TWnPOyww8wOO+zgrlDq9JxVTsNnZ7Y6sOyxxx7uCnFBvACljMQ/AskmeKeFRM+ePW3iPSoaWO+77z5bhRo1DdQbbLCBuwpGE+hCtjdUpe4LL7xgK3eBQlPLwjZt2ngVyKhAReOMKifjSgU8kydPdleIyqJFi7yCxwr8MsEG4k3PgB49epi5c+e6VwpPQQS1W+7Vq5d7JZgjjjjC7LTTTu6q+PBMx6p0FniVKlXcVWYzZswoeAG0PncK8saZChKrVq3qrjJT54S4Jf5VBLLxxhu7q8y0466Q/wafz6kogKuYQ6Gknjk+5w3nm3Y5KvnvQ7EinTUf5/E+KWrWrGmuvfZaryMXUvR9OO+883iuwVKSqUOHDu4qmLjdyxoj1X1WxaRBaQw79NBDac8OS58hJYp1tn9QKqI69thjOdc/hogXoJSR+Ecg2QTvRAl3Jd4LuRhOURJbVZ6+A2s+1a5d2/0sGJ1J9dVXX7mr/NKDSOff3HXXXe4VoPBUIXvwwQe7q2DUolA7HaIsMiqPzlXVPXzkkUfaoGWpWbFihZ1cx+V8WQUjZs6c6a4y23777d3PAMSZdjyqDWNU46x2ynXr1s1dBaMAo3bnFXuAkWc6UpTorVGjhrvKTPf1hAkT7PqkEPR5u/3227124UTBt5B83rx5sWuVv/baa9vkf1Dvv/++Wbx4sbvKPyW+fGIeSg4Uctd/Ns+cfFtjjTVscHq33XZzrwSj8f766683n332mXsF2apbt665//77s07+q3Dg7bffdq+gVClp2bZtW++W/6m5WxzmRxojVYjg08H0mGOOMfXr13dXKHWag/p8hjTunnLKKTZvgngiXoBSReIfgWUTvBMl3pWAL+S5T/q7dD6jAjhxstVWW3kdmaAJtNrS5Pu9U1Bt3Lhx3hNkIGwKtGlyk02R0VVXXRWbYLx2l3fv3t0uAObMmeNeLS3qVqIqaQUB9H5EScVnPm3aFLj0GasBREvPAAWtC50sVpBcf6+C5j5KJcDIMx0pCobWqVPHXQWjOUQhduf89NNPNhgYhw5xmShp7rPjX0nzOLSDX5UCmD5nlaoDXiF3kqp1+q677uquMlNnCsU6li5d6l7Jn3feeceu132fOYWw7bbbmjPPPNNdBaeduddcc03kyX+1Blf8KMlFCEr+33DDDTZZ4EtFTyrC0GcMpU0dJHROeTZztyuvvDKS40pTshkjdbTBcccdZwuYAK0l1X0s6GdI94nWLBp/EW/EC1CKSPwjMD3QNCHynQDK1VdfbSuQly9f7l7JHy3aFCi64oorYpfEViKpUaNG7ioYtZzUTvx87XhJtZy57LLLYhlEQOnZc8897RlrvjSRu+SSSyJtM6fxZ/DgwbbdpQqPKKQx5s4777Tvh94XvT9RUNJfwbyg9tlnHxL/QMLoGaC5TCECjpo7TZo0ybZ19N0hrF0h2jVeKgFGnukQtajfeeed3VUwqd05+QzQ/fDDD+bGG2+MVdv0TJRg9TF27NhYfXZ17IPPHEtfu85pLtQcctNNNzUNGjRwV8E8+eST5plnnslrsb4CxxdffLHdGBBH2incrl07G6j2peT/aaedZqZOnVqwLh+rWrBggbn00kvNAw88EJtOZdlq3ry56dOnT1bJf322FLf74IMP3CsoVS1atDAnn3yyuwpOR4bq6IhCF5yl5uXnnHOO1xip2Pbpp59uatWq5V5BKUttINQaJCgVru29997uCnFHvAClhsQ/vDRr1iyrCaDcdNNNtrVJPnd+6s9WhacWxRUFOLSTUxV8Udhoo428E//6d+jfpAls2AthBVAUqDj77LNJ+iM21MJUwZ9sAhYKHJ100klmyJAhBe0yoiCRglWqjtcYyY7Af9L7ofdF74/ep0IG1RQo1ZgfNOitAIAm2rTUApJHAccTTzwxr8mDVFBIf4/vWK/xRePgNtts414pfjzTkaJdK7vssou7CkYBOj3Df/75Z/dKeFRUcv7559vd2kni20FOBd5KnMeJ73FKgwYNKthOZBUmNGzY0F0Fp+IgPYPCnuPqzxs6dKjdTR/3oyj0jNM9le2Oc3WI0bnchTomUn+P/j7t+FXhRrFQp07t/M9mw45iTlEX3SF6Ggc1d8vm6Ag9bzp16mReeOGFghRs6e/o27dvVvPyCy64wBYsAaIjvXy6BuuZpWNuSM4mC/EClBIS//CiCaACYNlMAEVt/48//njz+uuvh7oo1qCqCaYqojKd6a/JnW8Vf1h0LqOqZ30XYUrKq0ps2LBhob1vqcr2dEUSej858x9RUGBY92o2NLFSouCiiy6yP8/XZE7UxUQ7qTSuHXjggXZnICqm90fvk94vvW/57AKjsVKLN98KWx1po4AZgGRKJQ/uu+++0Fsva+6kXQLaHbRw4UL3anB6Nh100EF2Z2Qp4ZkOqV27dla7otT9TC0yv/vuO/dKbpQkUEHBUUcdZYtLyqO12r333hvLhED16tXNDjvs4K4y0zpPHQ3itItXhQs77riju8pMa+EHH3ywYMd/NG3a1Pu8er3PWlerkCSsZJc2NejILHVdrKhIX3GZOHWs0HifbdJZ76G6NippOGHChLwVfGluoKRky5YtzeWXX57V8zzONMfo2LGj7biZbfJfc52PP/7YvYJSpO4y2R4doXtKxUpKXqloK+yCKNGfqT9bf0fnzp2972OtFU499VSStrBU7OSzWUTPOj0/dDwQkod4AUoFiX940/mMmlxls4iQyZMnm/bt29tkjHZi5jIJTAXoVEV16KGHZkzu6O9UUifKAVRBjmxanmqxr0W/KrC/+OKLrAOfammjKsZMle0KyGgi7HOOJBAW3aPHHnusvWezpc+32h0q2aDzQcMKHunP+fDDD+3CQC2MFVhRUQ6C0/ul903vn44C0Bm0YX1/9EzRn6exUoFDnwpbPdeyPdIGQGHcfPPNNiGXjoI2Cla2bt0657OXNd/SAj41d1KnpGy0atXKPo901nmp4ZkOUQF5mzZtsnrG6j7W90YJ+2yLBpWMVUGgEv5a46TrdqbPq4JucaS1mRLTPpTIO/fcc80bb7zhtYbU71XLZiVJw6SuBeok6EPfe83t3nvvPfdKMJoXatPBa6+95l7JTF+fPqu+Usn/XJNdP/30k92JrueG5snpnHHGGTY+Exca73U8itofZ0vxIv0ZCsqrACuMoLy+F/PmzbNjvTZiKCnps0ZImly/D9pUc91115nPPvvMvYJSlEv3CNH9qyP0dL9NmTLFrFixwv1K9vRn6M/Sn6k/O5siTRVMqaCQpC1E3V8effRRr2Mili1bZtekOt4mzj/ieARyIRAvAP5C4h/ewljMiQJ4BxxwgNl///1tBb92IWQK5Ggw1eCsc1Kuv/56rwCdJnennHJK5AOoWp4qGZXt5FkPEO2W0cNg9OjR5scff0wbwNEiV7sjNCFWt4addtrJPowyVZ7pz2fXK6Kke1U7/BT0yYXGGu3oUJBUCzwF/r7++uvASQONS/Pnz7f3kIJ5+nP0Q5PEdEFjZKb3T0fAKPir91Tvr95nVVxrMRWUfq8CrHqWaHee/rxsJtsa9zijDYg3zUPVVlHBjEwU1NcuILVt1n81b9IOykzJGAUVNe4//fTTNkmoFuVB5k4V0W4p7QqpWbOme6X08EyHaBd1NgXQovtZCXslZFNrx0xJBH2/Z86caZOnWtdoDTZu3Dj3q+XTmlEJhfXWW8+9Ei/qIKe5iu9aUgXybdu2tXMdtTdNt+5WEFzrbd0jmleFvdNe763W8b7UoUFF/EpI6vOQ7vu/ePFiOz7oM6NNBz7HRWgHqP4f36MpUjS+KCGlv1s/1/uX7rmjtbzW9HpGqVV+aidhpjEpDpsayqP3T3GXXIq9RPdqKn6htuNqm6vxO0jyUO+3nvf6HKuDoe7rJk2alNRYr++DilDuuOMO94of3W96vwpxFjLiKazYb//+/W1yTWt0xXF1bwedu+n3aP6tYhT9v/oz9Gfpz8yG5iG33HKLqVu3rnsFpeyPP/6w6z3fzjl6jowYMcKOk3H+ofE707q3GBEvAP5SacmSJfnrlxgjWtiq4qdPnz7ulfRS58THic620wIqCC3Q9W/deOON3SvhU0Dg1ltvzdha35cGS1XZl6Xv4YwZM7KqVtMAqvdDO4VEO4UUNAxCE8PHHnssqxZXFdG/Re+d2q+FQV+bJq6rrfbPWh5VrE2cONFdBacW/wqQbbrpprH43EX9/cqGdmqcd955gXeNxWXMids4I0oCawLmU4EbVEXjjfzvf/8zs2bNynritipVkGYb6M6GFiLaAZSpC0o+7xff5255FNRu3Lix3SVYnlyeC2UpGdW9e/fEV/5rJ5OCdEEU6h72ldQ5m8/4mdRnVT7Gsmy/37k8G9KNLRrzNe8Ii77HPXr0sIWuhUrOxOH7WhGe6VDS+eyzzw4t+aYEqwqrV6VgnT5rvn+HxgYdLdChQ4dY30dKaquNaLaJj5Ty3rvyxsB8PGcVLNXnIJexoKKxXN3xyu7m9v3+KBmgHYBXXnmleyU36tSgoPKaa67pXvlLtnNZJbIfeOAB2447rmtlFVvoqALdU2HT119e/EOyjYGE9d4UW9yuWNZIcZHEtZrGKRXc3XTTTe6V8Kj4sqIuo2HPyTVP1C7gQm5wSuq6tlSow4zmesVaEJbLGBKnzy7xgvyLQwwZ4WPHP7IW1s6dsrRIL69STVWh2Sb9tdCJ0+51PThUva4Fexg0QJdXbZjNgldf09VXX22T/kAcKKijnQph3S+rqmi80Y9Ro0aFkiBA9jTma+wv7/ujH9k+F8rSZ4t2f0Cy6NmgwGk2i850Y0uYi3gFMhUkjXIRHzc806EgmnbUh0XrnbLfb62LsgnialejgqRxt9FGG4XydZb33oU5BqazxRZb5PxvqGgsL5v0z4Y6K6hQIKxYh8YfjUNlv9Zs5rJ67un5p6R/nK2//vp2fq2YUdgqin/oRzYxkGKmuF2XLl2y7sCgYzauuuoq8/3337tXUGoUv1Q3EhXyhE3PnPLuY/0I83mkead2ddPVFCnqxnP33XcXbdIfxAsAEv/IiZIkmvyFnfwPSyrpH8cWeLk8gPJFk2EFY/W1AXGy66672up4nZcEhEmfKe2AYdwDkkfBO82lVJEfN5rfaWw59NBDWcSXwTO9tIXVBjxsCrqpNbu+viTQDu8gLUzjSol1dVaI8zigWIcS1/koVMqWni3aFZaU5FUq+a+jveL4rC4VuW7aUfJfR2yQ/C9dlStXNuecc455/PHHK9yhH1d61qiDi+afgKgTirrRqCAPxY14AUoZiX/kTOePqEouaDuzQlEbp3vuuSeWSf+UOD2A1K5FZ10xGUZc1atXzy7Y4jbWZKIWoS1atHBXiBMda6J2YXXq1HGvAEgSze86duxoAzdxCkJqTqXnlc7TZhFfPp7ppS1fneOypcSkEhrltfOMK60f1ZIzTkXkvmrVqmVOP/30WCeE41Ssr69BmxqStitM99UFF1xgW4Un+fOadCpkUcv+bMfd559/3hZw/PDDD+4VlBoVxunc7H79+tm5bhKok4/Gni233NK9glL3559/mpEjR9qz2VH8iBeglJH4RyjUFl6LiLhUcmvg1EM87oviuDyA9H498sgjpkmTJu4VIJ6qV69uxxoVG8U5SCjNmzc3Q4cOtcHkzTbbzL2KONBnR+d+qbqWIACQbJpLqUpeZ82p6DNqZ511lg2OM6fKjGd6aUsloaLcta7PnbpPXHLJJbYYIWl0NnJcdzEFpXb/SszEme5/JY6ifMYoQPzwww/HelNDOjqLv3379ubFF180nTp1cq+i0DTuqu1/tp02nnrqKTtu//TTT+4VlBqNP7vvvrvp379/7Dr3rCo1b9MxFeo8AqR8/vnndvNHGEdGIhmIF6BUkfhHaFTJrYmfqj81yYqCgh5ayGgwT0rb5tQD6IUXXojkfdP3TIEM2lwjKTTW6GzYYcOGxTJwpImkKjcHDx5sdwUq0FWKNLapJWDc6DOjz452GiYxyA/g3zTeqNhTRZ9RPRc09vft29fuxlRCG8HwTC9tSkKpQ5vWb4VOXut7qzFD7f3jOF8JQmPfIYccYu66667EJv+1g1TfAx21EGfq1BfVM0Ydqp555hmbbNP3PMkUc9CGAz0v4xB8T9H39b777jPbbrute6V4qdOZjovI9ggLnZOugj21ykbpUhGkOoYqua45eFxoQ5U+n8zbUJGVK1ea33//3V2hVBAvQCniCYhQaSDde++97SRLk61C7mLXglhBQ7XgzFTR6bNI2Xjjjc16663nrvJD75sqvZ577jm746EQgZtUBawm6/o3Akmie2aXXXaxgSONN1EVG61Kk0hN4saMGWOOPvrokk8qr7322ubGG280o0ePtuNz1PT9eeWVV+y5hPrsJD1wCuDflFBQQFoB7ULNQfX3qOOVxhcFEZKaQIwSz/TSpnXbFVdcYddBhfjea52l9ZbuWX2fkz4fUOJcn1EFMuOUSPWhAqDOnTvH/uxoPWNUMF+oOEcqQKydicXUoUrPST0vX3vtNfu8jrL9v76O4cOHl9z6QJ9lrdOyHTPUNU2JC5L/pU1JdSXX1clD8zc9U6OSmo9PmjTJ7qZl3gagPMQLUEpI/CMvNMnSZOvtt9+2C+N8LeYUuNEOgbFjx9rdOEEXaz7nkmlALtSgrKrZq6++2gYZtfspHwUAjRo1sgtbKmBRDHRvtmzZ0hb9KGijM+cKueNJwZLrr7/evPXWW/ae0iSOReb/0fii3UnqwjJnzhw72S1kUFoTbLXvTX1/9t13XxsgB1C8UjvIFfjTmJOvBb3mU9odOGXKFJuwov177niml65U8kDvu9Ypur/Cps+Sxgats7TeKqZ7VuvfVIFjPorIC7EW1vxMhaLjx4+36/sw6f0I69+QinNMmDDBvtf5eMYodqIYisbBYg4Qb7DBBvaefPPNN22Bw0EHHeR+Jb/0/l522WV2rH/yySftxpVSXB+oi4U6rmQbq1PyX23/Sf4jNX8bOHCgfcZqDC/U/C1VqDlr1iw7H2cXLYBMiBegVFRasmTJn+7nQN4sX77czJw507z66qt2l/knn3zifiU7WhTqbPzWrVtnNUAPGjTInHLKKe4qPZ07qCr7KHbFL1y40FbCq4J23Lhx7lV/eo/0fh1++OH2fMBiDR4AovvmjTfesOONFp66DosCI0pk77PPPvZsxM033zyWxTMaY8844wwzffp090r5NB4oKZ+v4qzyqLXa119/bQu2Ro4caV5//fVQz1fTebdt2rQxBx54oE3irLXWWu5XAMSR5og333yznWsF0bVrV3PxxRe7q8yWLl1qxxvN/ZRUzIXGlMMOO8y0atXKNGjQgEKiAuCZXprUglVrx5deeskeI5fL913trFVE0rZtW1OzZk33avH6888/zZdffmkTMEqGZLvu1vrxhBNOMMccc4ypV69eQe8NzRU//PBDe/7ps88+m/X3X/f4ySefbNfA2jGfj93cYT1jlCTTs0XvtxLRpVh0pM/u999/b9/PUaNG2R9hrREOOOAAmyBUgRHrAyD/VBCiZPyIESPsvaxNAGHQs0lFBgcffLDZc8897ZFBpdKpAyhVxAvyL84xZGSPxD8KToGcb775xrz33nt2Qf/uu+/aHfgzZsz418JOgThVgu+8885mp512sueR6Yeqs3LRu3dvc+2117qr9M477zzbBi3XvzNXehB99NFHZvbs2XYCrffwiy+++NcEWg+Zrbba6u/3TA8aXbO4RSnSeKMA0qeffmref/99M3fuXHvvKIA4bdo097v+j4JujRs3tve7gsNqA7XNNtvYYOHWW29t29EmYWGZpElb6nv0+eef2zFOwWqNcwr66rq8gLWS+1r0b7LJJmbHHXf8+9mg71PUYzUAP/leyK+q7Fzqq6++KnecSY0xGhu33357O6fSz6tUqUJwMUKl+kwvdauuHXXv6seSJUv+tXZMfb+32GIL07BhQ7sG2mGHHWzxdql+n1Pvnbrw6X7Re1fe+nHVMU/vm46gi8v6ccWKFfZr1r9BnwGN2eWN22XjBvo36L4vZMBVz7OPP/7Yfp36oa+xvPFJ77PGI/3Q+60fYcQ4io2+999++62ZN2+efS8/+OCDCmMgwvoAiCcV9ei5/dlnn9n524IFC+zzKFUcULa4a9X5m8ZLzdl0T2+77bY20U/hLVBaiBfkn/59JP6LD4l/lBxNOtXSTA+NIC688ELb9lPnVQNAEgSdtIl2UGrSCgBRKORCHgAAAAAAJAPxgvxTcYNiyOq4lg6J/2ShlyFKzq+//urVLlAVXCT9AQAAAAAAAAAAUAwWL16cMekv6qS23nrruSvEHYl/lBwl/tUeLii1hgOAJKlcuXLgyZha7QEAAAAAAAAASoeOUgpCsWb9QDKQ+EfJWbRokfn666/dVWba8Q8ASaKkv845DWL+/PnuZwAAAAAAAACAUhA0Lqwc2VprreWuEHck/lFylPQP0r5EdtxxRxL/ABJHx5NstdVW7iq9Tz/91CxbtsxdAQAAAAAAAACK2fLlywN3xt50003Nmmuu6a4QdyT+UXJmz57tfpaZEmfVq1d3VwCQDEr8By1a0pj47bffuisAAAAAAAAAQDFbuHChee+999xVeptvvjk7/hOExD9KypIlS8w777zjrjKrW7du4HOyASAuKlWqZMevIKZPn26mTZvmrgAAAAAAAAAAxeztt982b775prtKb/vtt3c/QxKQ+EdJ+fLLL827777rrjLbeuut7c5ZAEiaOnXq2ONKghg1apRZvHixuwIAAAAAAAAAFCPFgYcNG+au0mvWrJmpXbu2u0ISkPhHSZkxY4Z5//333VV6G264odl1113dFQAki44q0cQsiP79+5vhw4ebP//8070CAAAAAAAAACgmiv8OHDjQxoOD2G233UyNGjXcFZKAxD9KhqqYxo0b564ya9q0KZVMABJLx5Tsueee7iqzu+66y7z66qsk/wEAAAAAAACgyKxcudIMGTLE3Hbbbe6VzFq0aGHWWWcdd4UkqLRkyRIi/CgJ48ePNyeeeKL573//615J77LLLjPXXHONWWuttdwrAJAs8+fPN2effXbg85rU6eS6664zxx13nNlggw3cqwCQP8uXLzc333yz6dOnj3slva5du5qLL77YXQHxpmPG9CwuFfXq1TObbrqpuwIAFLt58+aZRYsWuavitsYaa5iddtrJrL/++u4VILl+/vlnM3fuXPP777+7V4rbZpttxvnkCUW8IFx6Zj/66KP2/QyaI2vTpo3p1auXqV69unsFSUDiHyVh6dKlNpn15JNPulcyGzBggGndurW7AoDk+eOPP8yDDz5orr32WvdKMNttt5059thjTatWreziSN0DACAfWMijmA0aNMiccsop7qr4jRkzxnZNAwCUhp49e5obbrjBXRU3tTl+7LHH7FoZSLpPPvnEnHHGGWb69OnuleLGGjK5iBfkbtmyZbZQb+TIkTbpv3DhQvcrwTz00EM2RlypUiX3CpKAVv8oCWPHjrWBt6AOPPBAs8suu7grAEim1Vdf3XTo0MHst99+7pVgtAjs1q2b2XfffU3NmjVNlSpVTLt27cw777zjfgcAAAAAAAAAIE4Uv1UcV/FcxXUV31Vrf9+kv2LKLVu2JOmfQCT+UfQWLFhgHn/88cDtS0TnYletWtVdAUBy1apVy5x//vm2jX8uJk6caFasWOGuAAAAAAAAAABxovit4ri5UIeb8847jxb/CUXiH0Xtl19+se1IdL5/UBrU1N5aO2UBoBioOvOaa65xVwAAAAAAAAAA/JM2j+konz322MO9gqQh8Y+i9fvvv5unnnrK9OrVy70SzCGHHGJ22GEHdwUAybfGGmuYU0891dx0003uFQAAAAAAAAAA/qKkf5cuXWyOjBb/yUXiH14+++wz89xzz9md9HGmpP+AAQPM7bff7l4JRrv9Dz/8cFO5cmX3CgAUh3XWWce2/O/Zs2fObf8BAAAAAAAAAMVBR1/fc8895owzzrCbyJBcJP7hZeXKleaxxx4zBx98sBk8eLBZvny5+5X4+O2338yjjz5qrrjiCq9z/eWYY44x9evXd1cAUFxU1KSd/xq/mzdv7l4FAAAAAAAAAJSiTp062XjxEUccQdK/CJD4R1ZmzpxpTj75ZNOxY0czdOjQ2BQALFq0yHTt2tVcddVV3kn//fbbzxx33HEMbACKmto0NWnSxAwZMsT07dvXNGrUyP0KAAAAAAAAAKAUaGNYv379zCOPPGJ22WUX2vsXiUpLliz50/0cyOiTTz6xrT6mT5/uXvmLEkennHKKad++vW0JUmja5T98+HBz5513mjlz5rhXg1Pb6969e5sOHTq4VwCgNOhoFBVzvfzyy7aQS+N8RcaMGWOaNm3qrgAgdyoevfnmm02fPn3cK+mpwPPiiy92VwAAAAAAoBgRL8jOtGnTTMuWLd3Vv+m4a+XxDj30UJvXYyNs8WHHP0KhpNFFF11kGjdubP87depUs2LFCver+aOE1RtvvGGLDtSBIJukv1xwwQWmXbt27goASocmd0rm33LLLXZiqHH0hRdesJNltXdq1apVJAVdAAAAAAAAAAB/iucqrqv4ruK8ivcq7qv4r+LAigeT9C9O7PiHl4p2/JcnVTl08MEHm4YNG5p1113X/UpuVq5caRYsWGB3+D///PO26CAXhx9+uOnevbupVq2aewUAAACFQAU/AAAAAAAoi3gBkB12/CNvVCRw3333mTZt2pgaNWqYjh07mh49epjRo0eb+fPnm6VLl5o//0xfd6Id/YsXLzazZ882gwcPtgP3brvtZnbeeWd7jn+uSX+d69+lSxeS/gAAAAAAAAAAAAASi8Q/Cmbs2LG2Quuwww4zDRo0MFtssYU9W1+dAbTr/phjjvn7R/PmzU2VKlXMJptsYmrXrm322msv28r/iSeeSHv+tA8l/e+55x5Tp04d9woAAAAAAAAAAAAAJA+Jf0Ru4cKFZtSoUbZ1f+pHtmf1B9W2bVvbjYCkPwAAAAAAAAAAAICkI/GPknPKKaeYBx54wGyzzTbuFQAAAAAAAAAAAABILhL/KBlVq1Y1999/v7nrrrvMpptu6l4FAAAAAAAAAAAAgGQj8Q8vq622mlljjTXcVXJ06tTJvPTSS3a3f+XKld2rAAAAAAAAAAAAAJB8JP7hRe3xn332WdOtWze7gz7u9t9/f/PKK6+Yxx9/3DRo0MC9CgAAAAAAAAAAAADFg8Q/vFWvXt107tzZzJo1y/Tt29cm1+NGO/yHDx9uBg4caPbdd99EdikAAAAAAAAAAAAAgCBI/CNrG2ywgU2wDx482MyePdt0797d7LXXXu5XC09/t76GOXPmmKeeesrsvffeJPwBAAAAAAAAAAAAFL1KS5Ys+dP9HMjZn3/+aX766Sfz7rvvmsmTJ5vRo0ebadOmuV8NV/369c0ee+xh9ttvP/vfatWqmUqVKrlfBQAAAAAAAAAAAIDSQOIfebdixQqzcOFC88UXX5iPPvro78KAX375xb5eUWHAdtttZ+rWrWtWW201+/PatWvb/2611VZm8803N+utt577nQAAAAAAAAAAAABQukj8AwAAAAAAAAAAAACQYJzxDwAAAAAAAAAAAABAgpH4BwAAAAAAAAAAAAAgwUj8AwAAAAAAAAAAAACQYCT+AQAAAAAAAAAAAABIMBL/AAAAAAAAAAAAAAAkGIl/AAAAAAAAAAAAAAASjMQ/AAAAAAAAAAAAAAAJRuIfAAAAAAAAAAAAAIAEI/EPAAAAAAAAAAAAAECCkfgHAAAAAAAAAAAAACDBSPwDAAAAAAAAAAAAAJBgJP4BAAAAAAAAAAAAAEgwEv8AAAAAAAAAAAAAACQYiX8AAAAAAAAAAAAAABKMxD8AAAAAAAAAAAAAAAlG4h8AAAAAAAAAAAAAgAQj8Q8AAAAAAAAAAAAAQIKR+AcAAAAAAAAAAAAAIMFI/AMAAAAAAAAAAAAAkGAk/gEAAAAAAAAAAAAASDAS/wAAAAAAAAAAAAAAJBiJfwAAAAAAAAAAAAAAEozEPwAAAAAAAAAAAAAACUbiHwAAAAAAAAAAAACABCPxDwAAAAAAAAAAAABAgpH4BwAAAAAAAAAAAAAgwUj8AwAAAAAAAAAAAACQYCT+AQAAAAAAAAAAAABIMBL/AAAAAAAAAAAAAAAkljH/D/WYDk90/eJhAAAAAElFTkSuQmCC

base64转图片

希儿希儿希尔

Ch405是一名忠实的希儿厨，于是他出了一道这样的题，不过他似乎忘了这个加密的名字不是希儿了（x虽然经常有人叫错
补充：
图片打不开是正常现象,需要修复
最终得到的大写字母请用hgame{}包裹

我的解答：

宽高爆破

foremost分离文件得到密文

CVOCRJGMKLDJGBQIUIVXHEYLPNWR

根据题目名字希儿希儿想到希尔密码，但需要key才行。

图片放到随波逐流解出

RGB:KEY:[[8 7][3 8]]

然后希尔解码:http://www.practicalcryptography.com/ciphers/hill-cipher/

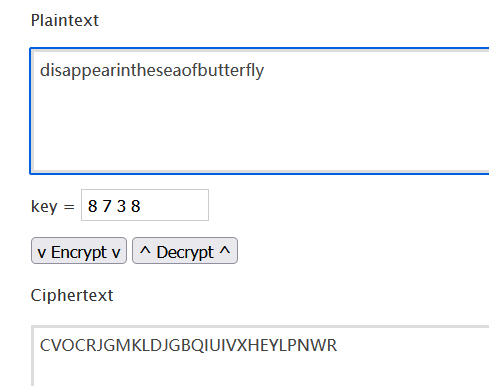
disappearintheseaofbutterfly

hgame{DISAPPEARINTHESEAOFBUTTERFLY}

签到

关注“凌武科技”微信公众号，发送“HGAME2024”获得 Flag！