RSA入门(二)
学习了RSA入门(一)之后,相信你已经了解并学会了RSA基础知识题型及操作,下面我们来在此基础之上学习延伸RSA各类攻击原理及其应用。以下面12道题目为例。(常见)
[RSA2]P1(小明文攻击)
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
p = getPrime(5120)
q = getPrime(5120)
n = p*q
e = 97
phi = (p-1)*(q-1)
m = bytes_to_long(flag)
c = powmod(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 1392208858696945158251408085300402884210409327605255122395601049457847957306648819174395014931778575812308192875319127224095733396726388842605854427013313599830150182564652493067830031524869535522568868597852507293377043240832819715539722122306829543983051745406887140154364256267942350230636870212935356815475345989038318923389132101208917912083817520799490534351545373438629367819085151041702754019127891155542476560972125790519584018715794669416759039955180436830478697704458250990786586357019211642837879273967620287257818400267757312623543898635740200839249361087580046496969637043238450499583879116276661827372750638403042213043389905183760455450595752578482968202040860053524276678108325784161897719093223308370971388068813420487879756084379519128232693549989942550047529174783976176943482484756074638704076740157397067892580297182979526978967352014250386678155843772313996171396582929433057131989693861316408604436872931427368192437680361830753162284661119995125858203931094922686321756465463988790748131178263745308042820480140189644732824717255521633534750635979508673908361269979175726073254050574688259969290376926807033728165164896588540691889207252105903436659968119091774687841336252628343233161941187968365128093917171537997137001140227677728923114895809278926486615010954871408034272872411042537353956193868948909981683850857262457369506288525323882308421700421661036191853577105238753230479541719001794464585534292774768292358961920606891227776349593589481547577148801600196035588544512224775960892265021565124673788852875005526313525709353599584812394138968970647681759439523307392275602626903789154682706839530654070108096741181206975334567778238856983205004289416400671597321919876279909765650782227834097342294844294386380646928266942749144240020420237153276705785759403019072953506982997681174635673907151856644499332322321579088035719680421458310273802481031746012298208449699089203065699598926690947025679591160106357130634946357609420125223580319677387654711233585375013067828291928349946599077331636017784447090096340360087970540477975170379810969501197027775838769222713506443846417124839450184827707739588007707714623211453528342755023849716924694572679150284882978804641986457119009272574734697043321033091757474387114449914271460113979531460465175717705674905568446670579332667139075523255580471183372714211547822093365025438653384719374474230360983878837077517864405475258349436531094649276628214288499716485354283135575921258757214288792410583835467572916298688718758374714560819702413058421373661892101033513816116981698045524150518509405086125781764762145577981637953775680403132163846782252745029783387112660812179706752454175492501665442704630131729362621965258498471247871904163412798544329515689112368523703890083138721480476796720323855371775568097188216621368341228806795058046403892301673157631331636430392885315997250027372621883549649614866115616619234953579196607399899485002042456482969222428121605212017146571466818179341621066715472184636758016242256725063854155219754299817717414423725704356940589670902509021070871847017199593680033
e = 97
c = 79418540691422578656139651796213224829563266521211325595707569487401417030874358531413674275017334363641194166574500833916574827523075402219754470871728896772312056257743844227927800121160288525434484105786180547178403828613331285574461293211150728313415280329153597549251599876668080073528625299164784405291297754331374420687599875173508778209038236713812747215157059659564867241144529476211694011692007565732793105429228730285249025627762831080251661835294067942958070742202862164086250986988784472568266652325462247009294865764533077164470382743735937483173523682749295196383707694876943634298051820105410771024861599560176707940488888601355473498847493259474613261665538825299531665650233837474894442826242097663456648233384047622152817959729025415665280499618951478005159820575701483220155180955748454167435711033379910310483689839303198822665341421591234243891877857520663120183063591818656508336831518527692847950877186870610083654117153248336928856886934232488927132245720058243202637258025864487122393335118118013444397135476780564523166548571927547341556616683070253790368891423731046742936358877118104790084195711730135202600692806999992373490439385845158780392894927697171401722699273071306493916233696254958735540772870249139252741670476667099529502282392011715616110876451102234600267482991583515122052976378641894214562203326290939184469206074418127906704847146567350085797480500249400491003993809769407575997740985283755035509654310797061339563655229926356893455738361409861102662109994984398860070584568014471082484198504331014073023689622378943694856212172718725529473812336321642429261822836311084518735006587545920946664595488768239633950124822001162595168106106356115962424210028401369438479550293237915944302351566624339603616714683958384871326105542659559877758488581425288668613061792514360263277530824203967659102107889148367539858141289229124274098921748855341045565232484417195620758495861456624842263649414501657786484816662971421962216348340311859717286253287173293151613310383128702607971580042308515018120559903265609733911340589091613087560931098833849573462572181625894166772788435459280323623477689159384354671220634694792005231505741029567734616435905915192606539962414882105254409847885996949466940350184140166614950171110955365828033747003120697209120916652982201967537088553504504252785632280900095976870510754563400828951684036526240669112248351928072177486091157562600003336544767896806392523395037345770580482363058065676920013089896399387769312374871419827762872050800055872960573607645266626972865053489632548224840580503746879607167797904430560935476705014800973841917939689270919224595772574781478285359220463175042728750523639669204218676238297875644055563803457896409252533724486937378974745777400567080239687055154021761534918106133195512030935957251049812753269173090858930245212145938555697547499155977225759702066548720079477737104010668116693232798415289735481194922014811945312893853446826780868861295203942063380964100360870361328125
'''我的解答:
本题为小明文攻击例题
我们可以发现题目中的n很大,此时我们考虑使用暴力的方式分解n几乎是不可能的,但假设题目中的m如果很小的话,则有
me < n
那么此时便有c = me,也就是在取模的过程中没有丢失任何信息,则我们可以直接开方从而获得m。
这里我们需要使用gmpy2中的iroot开任意次方,用法为iroot(10, 3)代表对10开3次方,返回结果为(mpz(2), False),其中第一项为返回的结果,mpz为gmpy2包中对整数的封装类,看作一个整数即可,第二项代表这个数是否为完全开方的结果,例如10开3次方根
并不是一个整数,但gmpy2只会返回取整后的整数值,故通过第二项我们能够知道是否为完全k次方数。
例如iroot(9, 2)返回(mpz(3), True)代表9是一个完全平方数。
完整代码如下:
from Crypto.Util.number import *
from gmpy2 import *
n = 1392208858696945158251408085300402884210409327605255122395601049457847957306648819174395014931778575812308192875319127224095733396726388842605854427013313599830150182564652493067830031524869535522568868597852507293377043240832819715539722122306829543983051745406887140154364256267942350230636870212935356815475345989038318923389132101208917912083817520799490534351545373438629367819085151041702754019127891155542476560972125790519584018715794669416759039955180436830478697704458250990786586357019211642837879273967620287257818400267757312623543898635740200839249361087580046496969637043238450499583879116276661827372750638403042213043389905183760455450595752578482968202040860053524276678108325784161897719093223308370971388068813420487879756084379519128232693549989942550047529174783976176943482484756074638704076740157397067892580297182979526978967352014250386678155843772313996171396582929433057131989693861316408604436872931427368192437680361830753162284661119995125858203931094922686321756465463988790748131178263745308042820480140189644732824717255521633534750635979508673908361269979175726073254050574688259969290376926807033728165164896588540691889207252105903436659968119091774687841336252628343233161941187968365128093917171537997137001140227677728923114895809278926486615010954871408034272872411042537353956193868948909981683850857262457369506288525323882308421700421661036191853577105238753230479541719001794464585534292774768292358961920606891227776349593589481547577148801600196035588544512224775960892265021565124673788852875005526313525709353599584812394138968970647681759439523307392275602626903789154682706839530654070108096741181206975334567778238856983205004289416400671597321919876279909765650782227834097342294844294386380646928266942749144240020420237153276705785759403019072953506982997681174635673907151856644499332322321579088035719680421458310273802481031746012298208449699089203065699598926690947025679591160106357130634946357609420125223580319677387654711233585375013067828291928349946599077331636017784447090096340360087970540477975170379810969501197027775838769222713506443846417124839450184827707739588007707714623211453528342755023849716924694572679150284882978804641986457119009272574734697043321033091757474387114449914271460113979531460465175717705674905568446670579332667139075523255580471183372714211547822093365025438653384719374474230360983878837077517864405475258349436531094649276628214288499716485354283135575921258757214288792410583835467572916298688718758374714560819702413058421373661892101033513816116981698045524150518509405086125781764762145577981637953775680403132163846782252745029783387112660812179706752454175492501665442704630131729362621965258498471247871904163412798544329515689112368523703890083138721480476796720323855371775568097188216621368341228806795058046403892301673157631331636430392885315997250027372621883549649614866115616619234953579196607399899485002042456482969222428121605212017146571466818179341621066715472184636758016242256725063854155219754299817717414423725704356940589670902509021070871847017199593680033
e = 97
c = 79418540691422578656139651796213224829563266521211325595707569487401417030874358531413674275017334363641194166574500833916574827523075402219754470871728896772312056257743844227927800121160288525434484105786180547178403828613331285574461293211150728313415280329153597549251599876668080073528625299164784405291297754331374420687599875173508778209038236713812747215157059659564867241144529476211694011692007565732793105429228730285249025627762831080251661835294067942958070742202862164086250986988784472568266652325462247009294865764533077164470382743735937483173523682749295196383707694876943634298051820105410771024861599560176707940488888601355473498847493259474613261665538825299531665650233837474894442826242097663456648233384047622152817959729025415665280499618951478005159820575701483220155180955748454167435711033379910310483689839303198822665341421591234243891877857520663120183063591818656508336831518527692847950877186870610083654117153248336928856886934232488927132245720058243202637258025864487122393335118118013444397135476780564523166548571927547341556616683070253790368891423731046742936358877118104790084195711730135202600692806999992373490439385845158780392894927697171401722699273071306493916233696254958735540772870249139252741670476667099529502282392011715616110876451102234600267482991583515122052976378641894214562203326290939184469206074418127906704847146567350085797480500249400491003993809769407575997740985283755035509654310797061339563655229926356893455738361409861102662109994984398860070584568014471082484198504331014073023689622378943694856212172718725529473812336321642429261822836311084518735006587545920946664595488768239633950124822001162595168106106356115962424210028401369438479550293237915944302351566624339603616714683958384871326105542659559877758488581425288668613061792514360263277530824203967659102107889148367539858141289229124274098921748855341045565232484417195620758495861456624842263649414501657786484816662971421962216348340311859717286253287173293151613310383128702607971580042308515018120559903265609733911340589091613087560931098833849573462572181625894166772788435459280323623477689159384354671220634694792005231505741029567734616435905915192606539962414882105254409847885996949466940350184140166614950171110955365828033747003120697209120916652982201967537088553504504252785632280900095976870510754563400828951684036526240669112248351928072177486091157562600003336544767896806392523395037345770580482363058065676920013089896399387769312374871419827762872050800055872960573607645266626972865053489632548224840580503746879607167797904430560935476705014800973841917939689270919224595772574781478285359220463175042728750523639669204218676238297875644055563803457896409252533724486937378974745777400567080239687055154021761534918106133195512030935957251049812753269173090858930245212145938555697547499155977225759702066548720079477737104010668116693232798415289735481194922014811945312893853446826780868861295203942063380964100360870361328125
m = iroot(c, e)
print(long_to_bytes(m[0]))
#NSSCTF{small}这类题目类型如何判断呢?当我们发现题目中n特别大的时候(e很小的时候),可以考虑使用小明文攻击。
[RSA2]P2(低加密指数攻击)
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 3
phi = (p-1)*(q-1)
m = bytes_to_long(flag)
c = powmod(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 111573371787314339229652810703380127177507745009618224416171957526984270337589283887959174610818933914845556276472159360153787395638087723501889651641965684241070152541291185349571453536221312112508437223801640552330390095266644485311958102687735113533739324296417077804219395793942670324182191309872918900717
e = 3
c = 90782646242308381145716338972639920044710403094882163620436540965475107006005657722222634294458956650085252212452241377251397323707019480880284004845674260662647720809672266571040936376737882878688872281858048646517100139303896804340224961592424635124272549514473232731744884837572128596217771005209683966262
'''我的解答:
本题为低加密指数攻击例题(即e很小,为低加密指数)
和上一题一样,可以发现题目中的n很大,此时我们考虑使用暴力的方式分解n几乎是不可能的,但我们直接使用上题的方式开方发现也不行,则说明me>n,不能直接开方。
我们有:c ≡ me(mod n)
消去取模,有:me = c + k⋅n
因为本题中加密指数e很小,我们可以考虑me的值并不是特别大,则我们可以通过遍历k的方式将取模后丢失的信息找回来,遍历到何时停止呢,当c+kn是一个完全e次方数时,则说明我们得到了正确的答案,此步骤我们可以用上一题中的iroot函数完成。
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 111573371787314339229652810703380127177507745009618224416171957526984270337589283887959174610818933914845556276472159360153787395638087723501889651641965684241070152541291185349571453536221312112508437223801640552330390095266644485311958102687735113533739324296417077804219395793942670324182191309872918900717
e = 3
c = 90782646242308381145716338972639920044710403094882163620436540965475107006005657722222634294458956650085252212452241377251397323707019480880284004845674260662647720809672266571040936376737882878688872281858048646517100139303896804340224961592424635124272549514473232731744884837572128596217771005209683966262
for k in range(100000): #遍历的范围
cc = c + k*n
res = iroot(cc, e)
if res[1]: #这里的res[1]的值其实是true或false
m = res[0]
break
print(long_to_bytes(m))
print('k:',k) # 11
#NSSCTF{i_think_small_e_is_not_safe_enough!}我们最后打印k会发现值为11,也印证了我们之前所说的me不会特别大,我们可以在一个比较小的范围(10w,100w,1000w对于计算机来说都算比较小)进行爆破k的值得到正确的答案。因此可以总结:当发现题目中e较小时,可以考虑此种攻击。
[RSA2]P3(Rabin算法攻击)
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
p = getPrime(256)
q = getPrime(256)
assert p%4 == 3 and q%4 == 3
n = p*q
e = 2
m = bytes_to_long(flag)
c = powmod(m, e, n)
print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')
'''
p = 67711062621608175960173275013534737889372437946924512522469843485353704013203
q = 91200252033239924238625443698357031288749612243099728355449192607988117291739
e = 2
c = 5251890478898826530186837207902117236305266861227697352434308106457554098811792713226801824100629792962861125855696719512180887415808454466978721678349614
'''我的解答:
❤ 本题为Rabin算法例题(特征:e = 2)
和上题一样,本题e非常小,有e=2,但我们会发现c不是一个完全平方数,则说明不能用低加密指数攻击的方法解决。小明文更不行。
同时我们也发现本题e和phi不互素,因为e和phi都是偶数,故我们也得不到RSA的私钥d。实际上,除了RSA算法外,还有很多的非对称加密方案,例如在本题中实际上使用了Rabin算法进行加密,只是它类似于RSA,故在CTF中我们将其划分到RSA攻击范畴中,在后续学习中我们还会遇到很对实际并不是RSA但类似RSA的加密算法。
❤ 在Rabin算法中加密流程为
1、取两个大素数(p,q)满足p ≡ q ≡ 3 (mod 4),有n = pq(这也是为什么本题有个断言
p%4 == 3 and q%4 == 3)2、加密过程为
c ≡ m2 (mod n)
我们会发现其实这就是本题的加密过程,同时它也等同于e=2时的RSA加密过程。
❤ 对于Rabin的解密,稍微复杂一点,这里我们需要了解二次剩余和欧拉准则,关于Rabin算法详细推导可见文章 Rabin攻击
这里也详细记录一下吧!
二次剩余
❤ 若p是素数,a不是p的倍数且与一个平方数模p同余,则称a是模p的二次剩余,记作a ∈ QR
例如22 ≡ 4(mod 13) 则称4是模13的二次剩余
同样我们把不等于0也不是模p的二次剩余的数称为非二次剩余,记作a ∈ NR
❤ 雅可比符号/勒让德符号: (p为奇素数)
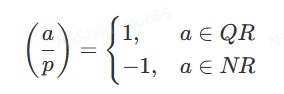
欧拉准则
❤ 设p为奇素数,则有
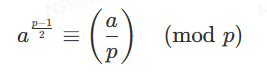
❤ 证明:
1、当a∈QR时,存在b使得
b2 ≡ a (mod p)
根据费马小定理可得
bp−1 ≡ 1 (mod p)
即
a(p−1)/2 ≡ (b2)(p−1)/2 ≡ bp−1 ≡ 1 (mod p)
2、当a∈NR, 同样根据费马小定理有
ap−1 ≡ 1 (mod p)
即
ap−1−1 = kp
所以有
p∣(a(p−1)/2−1)(a(p−1)/2+1)
因为a∈NR,所以p一定不会整除于a(p−1)/2−1,所以有
a(p−1)/2 ≡ −1 (mod p)
Rabin加密与解密
❤ Rabin本身是一种加解密方法,与RSA类似但这个函数不是单射,一个密文能解出4个明文
取两个大素数(p,q)满足p ≡ q ≡ 3(mod 4)
加密:
c m2 (mod n)
解密:
因为p,q∣n, 相当于求解
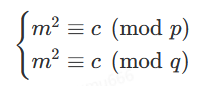
1、对于m2 ≡ c (mod p)来说, c是模p的二次剩余
即:c(p−1)/2 ≡ 1 (mod p)
带入原式得
m2 ≡ c ≡ c(p−1)/2∗c ≡ c(p+1)/2 (mod p)
开方得
同理可解另外一式得(m3,m4)
明文为四个中的一个
疑问
❤ Q: e=2且能知道(p,q)为什么不直接求d
A: 如果考的是Rabin攻击,则(p,q)满足p ≡ q ≡ 3 (mod 4)
则
φ(N) = (p−1)(q−1)
= (2k1+2)(2k2+2)
= 4k1k2+4k1+4k2+4
显然有4∣φ(N),所以e与φ(N)不互素,无法求出d
❤ Q: 四个明文,具体是哪一个?
A: 无从得知,根据明文含义即题目说明判断。
由此文我们可知Rabin算法适用于这种e=2,p,q已知且满足%4=3的题目中。此时我们可以通过Rabin算法解得四个明文,再一一测试即可得到最终正确的明文。
exp:
from Crypto.Util.number import *
from gmpy2 import *
p = 67711062621608175960173275013534737889372437946924512522469843485353704013203
q = 91200252033239924238625443698357031288749612243099728355449192607988117291739
e = 2
c = 5251890478898826530186837207902117236305266861227697352434308106457554098811792713226801824100629792962861125855696719512180887415808454466978721678349614
def rabin_attack(c, n, p, q):
c1 = powmod(c, (p+1)//4, p)
c2 = powmod(c, (q+1)//4, q)
cp1 = p - c1
cp2 = q - c2
t1 = invert(p, q)
t2 = invert(q, p)
m1 = (q*c1*c2 + p*c2*t1) % n
m2 = (q*c1*t2 + p*cp2*t1) % n
m3 = (q*cp1*t2 + p*c2*t1) % n
m4 = (q*cp1*t2 + p*cp2*t1) % n
return m1, m2, m3, m4
ms = rabin_attack(c, p*q, p, q)
for m in ms:
print(long_to_bytes(m))
#NSSCTF{rabin!rabin!rabin!not_just_rsa!}[RSA2]P4(Wiener攻击)
题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
p = getPrime(256)
q = getPrime(256)
n = p*q
d = getPrime(128)
e = inverse(d, (p-1)*(q-1))
m = bytes_to_long(flag)
c = powmod(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 6969872410035233098344189258766624225446081814953480897731644163180991292913719910322241873463164232700368119465476508174863062276659958418657253738005689
e = 3331016607237504021038095412236348385663413736904453330557803644384818257225138777641344877202234881627514102078530507171735156112302207979925588113589669
c = 1754994938947260364311041300467524420957926989584983693004487724099773647229373820465164193428679197813476633649362998772470084452129370353136199193923837
'''我的解答:
❤ 本题为Wiener攻击例题
我们会发现本题生成密钥的流程有些不同寻常,一般我们都是选定e,再通过求接逆元的方式得到d,而本题则恰恰相反,先选定d再来获取e,那么这种方式会导致何种问题呢?
我们知道有
ed ≡ 1 (mod φ(n))
即ed−1=k⋅φ(n),我们两边同时除以dφ(n)则有
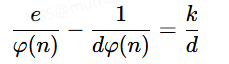
此时我们引入近似的概念,因为φ(n)=(p−1)(q−1)=n−p−q+1,所以其实φ(n)≈n,同理1/(dφ(n))是一个非常小的数,我们忽略不记,则有
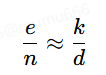
那么如果我们能够找到一种办法使得e/n转化为k/d则便能够得到私钥。Wiener便证明了当
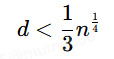
时,可以通过对e/n进行连分数展开精准覆盖k/d。
关于更详细的介绍可以查看wiener攻击
❤ 至此我们需要知道的是,当发现d比较小时可以使用wiener攻击,但有些时候我们并不知道d的大小,不过我们能够知道此时e会很大(因为ed−1=kφ(n),一个小另一个就大),所以其实当我们发现e很大或者说很接近n时,便可以考虑使用连分数展开的方式,遍历每一个系数,测试是否是解题中需要用到的关键因子,这种方式在很多题中还会遇到。
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 6969872410035233098344189258766624225446081814953480897731644163180991292913719910322241873463164232700368119465476508174863062276659958418657253738005689
e = 3331016607237504021038095412236348385663413736904453330557803644384818257225138777641344877202234881627514102078530507171735156112302207979925588113589669
c = 1754994938947260364311041300467524420957926989584983693004487724099773647229373820465164193428679197813476633649362998772470084452129370353136199193923837
class ContinuedFraction():
def __init__(self, numerator, denumerator):
self.numberlist = [] # number in continued fraction
self.fractionlist = [] # the near fraction list
self.GenerateNumberList(numerator, denumerator)
self.GenerateFractionList()
def GenerateNumberList(self, numerator, denumerator):
while numerator != 1:
quotient = numerator // denumerator
remainder = numerator % denumerator
self.numberlist.append(quotient)
numerator = denumerator
denumerator = remainder
def GenerateFractionList(self):
self.fractionlist.append([self.numberlist[0], 1])
for i in range(1, len(self.numberlist)):
numerator = self.numberlist[i]
denumerator = 1
for j in range(i):
temp = numerator
numerator = denumerator + numerator * self.numberlist[i - j - 1]
denumerator = temp
self.fractionlist.append([numerator, denumerator])
a = ContinuedFraction(e, n)
for k, d in a.fractionlist:
m = powmod(c, d, n)
flag = long_to_bytes(m)
if b'NSSCTF' in flag:
print(flag)
#NSSCTF{e_is_so_huge}[RSA2]P5(低加密指数广播攻击)
题目
from Crypto.Util.number import *
import os
flag = os.getenv('FLAG')
m = bytes_to_long(flag.encode())
e = 127
def enc():
p = getPrime(512)
q = getPrime(512)
n = p*q
c = pow(m, e, n)
print(f"n: {n}")
print(f"c: {c}")
def main():
while True:
opt = int(input('input> '))
if opt == 1:
enc()
main()我的解答:
❤ 本题为低加密指数广播攻击例题
本题为交互题目,每次交互我们会发现程序会生成一组公钥来加密同一个明文,并且这些公钥中的e都相同,则我们有
ci ≡ me (mod ni)
并且我们可以无限次交互获得足够多的数据,那么我们是否能够恢复m呢?考虑将me看作一个整体,因为它是不变的。那么问题则变成了给定一个数取模不同数的余数,问原数几何?此问题可以追溯至《孙子算经》中的问题
今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
答曰:‘二十三’。
术曰:三三数之剩二,置一百四十;五五数之剩三,置六十三,七七数之剩二,置三十,并之。得二百三十三,以二百一十减之,即得。凡三三数之剩一,则置七十;五五数之剩一,则置二十一;七七数之剩一,则置十五;一百六以上以一百五减之即得。
虽然我们要求解的数变大了,但方法是通用的,对于上述同余式,我们有通解
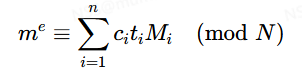
其中
N = n1n2…nn
Mi = N/ni
Miti ≡ 1 (mod ni)
我们称其为中国剩余定理(Chinese remainder theorem, CRT)。
❤ 则我们可以通过CRT得到me的值,再通过开e次方即可得到m的值。
❤ 但本题还需要考虑数据交互的问题,一般我们使用pwntools进行交互,是的虽然这是一个供pwn交互的包,内置了很多pwn相关的函数。。。但不影响我们在Crypto中使用它作为交互包。
因为一些底层依赖的关系,在windows上直接安装pwntools并不友好,故我推荐在Linux 虚拟机或者WSL子系统中安装pwntools。
你只需要pip install pwntools即可。
exp:
from gmpy2 import *
from pwn import *
from Crypto.Util.number import *
def crt(n_list, c_list):
n = 1
for i in n_list:
n *= i
N = []
for i in n_list:
N.append(n//i)
t = []
for i in range(len(n_list)):
t.append(invert(N[i], n_list[i]))
summary = 0
for i in range(len(n_list)):
summary = (summary + c_list[i]*t[i]*N[i]) % n
return summary
io = remote('node4.anna.nssctf.cn', 28820)
e = 127
n_list = []
c_list = []
for i in range(127):
io.sendlineafter(b'input> ', b'1') # 等待收到input> 后发送1
n = int(io.recvline().decode()[2:]) # 接收一行数据 即 n: xxxx
c = int(io.recvline().decode()[2:]) # 接收一行数据 即 c: xxxx
n_list.append(n)
c_list.append(c)
M = crt(n_list,c_list)
m = iroot(M,e)[0]
flag = long_to_bytes(m)
print(flag)
#NSSCTF{8b22817d-40b5-4e4a-ab0b-6b5fc95b832d}对于该包可以查看代码中的注释进行学习,事实上我们之后会经常在交互题中使用该包,此时我们只需要先手动连接靶机熟悉流程,然后按照思路编写交互脚本即可,不过需要注意的是,在交互过程中,不管是接收还是发送的数据,均应先转化为bytes类型进行操作(str字符串也可以,不过会提示警告)。
疑问?
问:这里为什么要循环127次呢,如何判断需要多少组数据才能通过crt求解?
答:可能因为e是127?我也不太懂。。中国剩余定理的要求,同余式个数不小于e
[RSA2]P6(p-1光滑攻击)
题目
from Crypto.Util.number import *
from random import choice
flag = b'NSSCTF{******}'
def getMyPrime(nbits):
while True:
p = 1
while p.bit_length() <= nbits:
p *= choice(sieve_base)
if isPrime(p+1):
return p+1
p = getMyPrime(256)
q = getMyPrime(256)
n = p*q
e = 65537
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 53763529836257082401813045869248978487210852880716446938539970599235060144454914000042178896730979463959004404421520555831136502171902051936080825853063287829
e = 65537
c = 50368170865606429432907125510556310647510431461588875539696416879298699197677994843344925466156992948241894107250131926237473102312181031875514294014181272618
'''我的解答:
❤ 本题为p-1光滑例题
这题和之前的题目也有一些不一样,在本题中,素数来自于我实现的getMyPrime函数,分析会发现,它的功能从sieve_base中随机选取数字进行相乘,直到得到足够多的位数为止。最后还要判断如果p+1不是一个素数则重复上述过程。
简而言之,我们将会得到这样一个素数
p = p1p2…pn+1
对于sieve_base,我们可以跟进查看其描述(在VScode中你只需要按住Ctrl+光标点击即可)。
# The first 10000 primes used for checking primality.
# This should be enough to eliminate most of the odd
# numbers before needing to do a Rabin-Miller test at all.注释中解释其是前10000个素数构成的数组,也就是说我们得到的p就是一堆小素数乘积+1的结果。
那么这对我们解题有什么帮助呢?在此我们首先要学习光滑数的概念。
当一个数的最大素因子组不大于B时,我们可以称其为B-光滑数,例如6=2*3可以称其为3-光滑数,12=2^2*3可以称其为4-光滑(因为2^2是最大的素因子组)数(注意我们也可以叫它5-光滑、6-光滑、n-光滑(n>3))。那么对于p来说它是p-光滑数(因为它是素数),但p−1包含很多小素数因子,我们假设p−1为k-光滑数,存在这样的一个数M
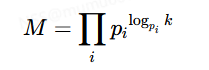
这个数有什么用呢,显然我们有
(p−1)∣M
这很显而易见,因为M中包含了p−1中的每一个素因子组。那么我们有
gcd(M,n)=p
也就是说如果我们能够得到M,那么便可以通过求解和n的公因数得到n的素因子。但是我们如何得到M呢?让我们一起来学习大智慧Pollard's p-1分解算法。
❤ 设M=t⋅(p−1),根据费马小定理我们有
aM ≡ at⋅(p−1) ≡ 1 (mod p)
即
p∣(aM−1)
同时有
M∣k!
这很奇妙,因为M中最大的素因子组不超过k,所以上式显然成立。所以我们有
gcd(ak!−1,n)=p
又因为p−1是由一些小素数相乘而来,所以k并不会很大,甚至可以说很小!我们可以通过遍历的方式计算每一个ax−1的值,如果它和n的公因子不为1也不为n,则我们成功分解了n。
❤ 在具体计算中,我们不需要每次计算x!的值,而是可以通过模的性质有
a(x+1)! ≡ (ax!mod n)x+1 (mod n)
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 53763529836257082401813045869248978487210852880716446938539970599235060144454914000042178896730979463959004404421520555831136502171902051936080825853063287829
e = 65537
c = 50368170865606429432907125510556310647510431461588875539696416879298699197677994843344925466156992948241894107250131926237473102312181031875514294014181272618
a = 2
m = 2
while True:
a = powmod(a, m, n)
p = gcd(a-1, n)
if p != 1 and p != n:
break
m += 1
q = n // p
phi = (p-1)*(q-1)
d = invert(e, phi)
m = powmod(c, d, n)
print(long_to_bytes(m))
#NSSCTF{p-1_smooth_with_factor}[RSA2]P7(p+1光滑攻击)
题目
from Crypto.Util.number import *
from random import choice
flag = b'NSSCTF{******}'
def getMyPrime(nbits):
while True:
p = 1
while p.bit_length() <= nbits:
p *= choice(sieve_base)
if isPrime(p-1):
return p-1
p = getMyPrime(256)
q = getMyPrime(256)
n = p*q
e = 65537
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 63398538193562720708999492397588489035970399414238113344990243900620729661046648078623873637152448697806039260616826648343172207246183989202073562200879290937
e = 65537
c = 26971181342240802276810747395669930355754928952080329914687241779532014305320191048439959934699795162709365987652696472998140484810728817991804469778237933925
'''我的解答:
❤ 本题为p+1光滑攻击例题
相比上题来说,本题的改动仅仅是将p+1换成了p-1,但这就造成了p+1变成了光滑数而不是p-1。而在p-1光滑攻击中,我们的关键点是
aM ≡ at⋅(p−1) ≡ 1(mod p)
但将p-1换成p+1便不再满足。
❤ 对于p+1光滑攻击,我们使用的是Willian's p+1光滑攻击算法,该攻击原理较为复杂,涉及多个引理以及复杂的推导,然而最终的结论却很简单,最终使用了扩展卢卡斯序列得到了一个p的倍数,再和n求解最大公因数进行因数分解。
详细原理及推导可以查看p+1光滑攻击
exp:
from Crypto.Util.number import *
from gmpy2 import *
from itertools import count
n = 63398538193562720708999492397588489035970399414238113344990243900620729661046648078623873637152448697806039260616826648343172207246183989202073562200879290937
e = 65537
c = 26971181342240802276810747395669930355754928952080329914687241779532014305320191048439959934699795162709365987652696472998140484810728817991804469778237933925
def mlucas(v, a, n):
v1, v2 = v, (v ** 2 - 2) % n
for bit in bin(a)[3:]: v1, v2 = ((v1 ** 2 - 2) % n, (v1 * v2 - v) % n) if bit == "0" else (
(v1 * v2 - v) % n, (v2 ** 2 - 2) % n)
return v1
def primegen():
yield 2
yield 3
yield 5
yield 7
yield 11
yield 13
ps = primegen() # yay recursion
p = ps.__next__() and ps.__next__()
q, sieve, n = p ** 2, {}, 13
while True:
if n not in sieve:
if n < q:
yield n
else:
next, step = q + 2 * p, 2 * p
while next in sieve:
next += step
sieve[next] = step
p = ps.__next__()
q = p ** 2
else:
step = sieve.pop(n)
next = n + step
while next in sieve:
next += step
sieve[next] = step
n += 2
def ilog(x, b): # greatest integer l such that b**l <= x.
l = 0
while x >= b:
x /= b
l += 1
return l
def attack(n):
for v in count(1):
for p in primegen():
e = ilog(isqrt(n), p)
if e == 0:
break
for _ in range(e):
v = mlucas(v, p, n)
g = gcd(v - 2, n)
if 1 < g < n:
return int(g), int(n // g) # g|n
if g == n:
break
p, q = attack(n)
phi = (p-1)*(q-1)
d = invert(e, phi)
m = powmod(c, d, n)
print(long_to_bytes(m))
#NSSCTF{p+1_smooth_number}[RSA2]P8(共模攻击)
题目
from Crypto.Util.number import *
flag = b'NSSCTF{******}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e1 = getPrime(16)
e2 = getPrime(16)
m = bytes_to_long(flag)
c1 = pow(m, e1, n)
c2 = pow(m, e2, n)
print(f'n = {n}')
print(f'e1 = {e1}')
print(f'e2 = {e2}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
'''
n = 120294155186626082670474649118722298040433501930335450479777638508444129059776534554344361441717048531505985491664356283524886091709370969857047470362547600390987665105196367975719516115980157839088766927450099353377496192206005171597109864609567336679138620134544004766539483664270351472198486955623315909571
e1 = 38317
e2 = 63409
c1 = 42703138696187395030337205860503270214353151588149506110731264952595193757235229215067638858431493587093612397165407221394174690263691095324298012134779703041752810028935711214038835584823385108771901216441784673199846041109074467177891680923593206326788523158180637665813642688824593788192044139055552031622
c2 = 50460092786111470408945316270086812807230253234809303694007902628924057713984397041141665125615735752600114964852157684904429928771531639899496987905067366415806771003121954852465731110629459725994454904159277228514337278105207721011579794604761255522391446534458815389983562890631994726687526070228315925638
'''我的解答:
❤ 本题为RSA共模攻击例题
在本题中使用了两组公钥(n,e)对同一消息m进行加密,经过观察我们可以发现这两种公钥的n是同一个n,不同的加密密钥e1和e2,也就是说模数相同,那么此时我们便可以使用共模攻击进行解密。
❤ 在此攻击中,我们需要两个使用了同样模数的公钥对同一消息进行加密,同时还需要满足公钥中的e互素(经试验,本题e1和e2满足互素)。然后我们考虑方程
s1e1 + s2e2 = 1
假设我们能够找到整数解(s1,s2)满足此方程,那么则有
c1s1c2s2 ≡ (me1)s1(me2)s2 ≡ me1s1+e2s2 ≡ m (mod n)
我们可以发现可以直接解得m而不需要对n进行因数分解,那么我们如何解得(s1,s2)呢?这就是之前为何要互素的条件了,根据翡镯定理我们有
ax + by = gcd(a,b)
该方程一定有且仅有一组整数解(x,y)。具体解法我们需要用到扩展欧几里得算法(在gmpy2中的gcdext)
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 120294155186626082670474649118722298040433501930335450479777638508444129059776534554344361441717048531505985491664356283524886091709370969857047470362547600390987665105196367975719516115980157839088766927450099353377496192206005171597109864609567336679138620134544004766539483664270351472198486955623315909571
e1 = 38317
e2 = 63409
c1 = 42703138696187395030337205860503270214353151588149506110731264952595193757235229215067638858431493587093612397165407221394174690263691095324298012134779703041752810028935711214038835584823385108771901216441784673199846041109074467177891680923593206326788523158180637665813642688824593788192044139055552031622
c2 = 50460092786111470408945316270086812807230253234809303694007902628924057713984397041141665125615735752600114964852157684904429928771531639899496987905067366415806771003121954852465731110629459725994454904159277228514337278105207721011579794604761255522391446534458815389983562890631994726687526070228315925638
_, s1, s2 = gcdext(e1, e2)
print(s1)
print(s2)
11253
-6800
m = powmod(c1, s1, n)*powmod(c2, s2, n) % n
print(long_to_bytes(m))
#NSSCTF{same_module_attack!}[RSA2]P9(dp&dq泄露攻击)
题目
from Crypto.Util.number import *
flag = b'NSSCTF{******}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e = getPrime(128)
d = inverse(e, (p-1)*(q-1))
dp = d % (p-1)
dq = d % (q-1)
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f'p = {p}')
print(f'q = {q}')
print(f'c = {c}')
print(f'dp = {dp}')
print(f'dq = {dq}')
'''
p = 13070310882303377463944295715444821218324151935347454554272870042925400761984585838979931730897626589859098834802923539617244712852188293321626061072925723
q = 10411551818233737389114520103233235272671271111546186997024935593000298916988792710521511848414549553426943998093077337023514210631662189798921671306236009
c = 62492280219693914005334023569480350249964827909276875032578276064973191654731196407886841145547165693859745313398152742796887457192397932684370631253099255490064673499746314452067588181106154875239985334051909867580794242253066085627399488604907196244465911471895118443199543361883148941963668551684228132814
dp = 11568639544706374912496682299967972464196129347160700749666263275305083977187758414725188926013198988871173614336707804756059951725809300386252339177953017
dq = 3455040841431633020487528316853620383411361966784138992524801280785753201070735373348570840039176552952269927122259706586236960440300255065994052962742469
'''我的解答:
❤ 本题为dp&dq泄漏攻击例题
这个题设计了两个我们之前没有遇到过的参数dp和dq,并且我们还可以发现,这道题没有给e(如果给了e我们就可以直接求私钥了)。其实严格来说这并不算一种攻击,我们首先需要知道dp和dq参数的意义,有
dp = d mod p−1
dq = d mod q−1
我们知道在RSA算法中,解密为计算cd mod n,我们可以来看一下它的效率
from Crypto.Util.number import *
from gmpy2 import *
from sympy import timed
p = getPrime(1024)
q = getPrime(1024)
e = 65537
m = getPrime(512)
phi = (p-1)*(q-1)
n = p*q
d = invert(e, phi)
c = powmod(m, e, n)
def work():
for _ in range(10):
powmod(c, d, n)
print(timed(work)[2])
#31.33492999986629这里我们使用sympy包中的timed来计算耗时(注意此函数会调用你的函数多次来测量平均值)。在我的电脑上输出31.33492999986629,实际上它运行了10此函数,一共解密了100次,似乎单次时间也并不是很高,但如果在一个频繁的操作场景中,如果我们能够更高效率的进行加解密,带来的提升将是巨大的。此时我们在解密时引入了dp和dq用于快速解密。
计算
m1 ≡ m ≡ cd (mod p)
m2 ≡ m ≡ cd (mod q)
根据欧拉降幂我们有
m1 ≡ cd mod p−1 ≡ cdp (mod p)
m2 ≡ cd mod q−1 ≡ cdq (mod q)
即
cd = m1 + kp
我们将此式带入m2的式子中有
m2 ≡ m1+kp (mod q)
即
(m2−m1)p−1 ≡ k (mod q)
此时我们再将此式带入m1的式子中即可消去k
cd = m1+((m2−m1)p−1 mod q)p
注意上式中模的位置,在同余中我们可以运算中途随意取模或最后再取模,但是将取模式转化到不同模或整数运算中一定要记得先取模且模数不能错。
我们会发现我们得到了一个cd的新算法,通过dp,dq,p,q即可解密消息,我们再来看一下他们的效率
from Crypto.Util.number import *
from gmpy2 import *
from sympy import timed
p = getPrime(1024)
q = getPrime(1024)
e = 65537
m = getPrime(512)
phi = (p-1)*(q-1)
n = p*q
d = invert(e, phi)
c = powmod(m, e, n)
invp = invert(p, q)
dp = d % (p-1)
dq = d % (q-1)
def work():
for _ in range(10):
m1 = powmod(c, dp, p)
m2 = powmod(c, dq, q)
m = (((m2 - m1)*invp) % q)*p + m1
print(timed(work)[2])
#9.506517000008898输出为9.506517000008898,显然可以发现较比之前快了4倍左右。实际上因为这种做法还缩短了每次运算的位数,在一些低功耗系统上表现会更优。
❤ 最后我们解密即可
exp:
from Crypto.Util.number import *
from gmpy2 import *
p = 13070310882303377463944295715444821218324151935347454554272870042925400761984585838979931730897626589859098834802923539617244712852188293321626061072925723
q = 10411551818233737389114520103233235272671271111546186997024935593000298916988792710521511848414549553426943998093077337023514210631662189798921671306236009
c = 62492280219693914005334023569480350249964827909276875032578276064973191654731196407886841145547165693859745313398152742796887457192397932684370631253099255490064673499746314452067588181106154875239985334051909867580794242253066085627399488604907196244465911471895118443199543361883148941963668551684228132814
dp = 11568639544706374912496682299967972464196129347160700749666263275305083977187758414725188926013198988871173614336707804756059951725809300386252339177953017
dq = 3455040841431633020487528316853620383411361966784138992524801280785753201070735373348570840039176552952269927122259706586236960440300255065994052962742469
invp = invert(p, q)
m1 = powmod(c, dp, p)
m2 = powmod(c, dq, q)
m = (((m2 - m1)*invp) % q)*p + m1
print(long_to_bytes(m))
#NSSCTF{dp&dq_leak}[RSA2]P10(dp泄露攻击)
题目
from Crypto.Util.number import *
flag = b'NSSCTF{******}' + b'1'*100
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
d = inverse(e, (p-1)*(q-1))
dp = d % (p-1)
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f'n = {n}')
print(f'c = {c}')
print(f'dp = {dp}')
'''
n = 79201858340517902370077926747686673001645933420450220163567700296597652438275339093680329918615445030212417351430952656177171126427547284822789947152085534939195866096891005587613262293569611913019639653984932469691636338705418303482885987114085769045348074530172292982433373154900841135911548332400167290083
c = 70109332985937768446301118795636999352761371683181615470371772202170324747707233792154935611826981798791499937601162039878070094663516868746240133223110650205575807753345252087103328657073552992431511929172241702073381723302143955977662087561904058172777520360991685289300855900793806183473523998422682944404
dp = 3098334089252415941833934532457314870210700261428241562420857845879512952043729097866485406309479489101668423603305497982177150304625615059119312238777275
'''我的解答:
❤ 本题为dp泄漏攻击例题
相比上一题,本题我们有了e,但是却失去了一个dq,此时我们该如何考虑呢?
对于dp我们有
dp * e ≡ 1 (mod p−1)
推导如下:
dp ≡ d (mod p−1)
dp * e ≡ d * e ≡ 1 + k(p−1)(q−1) ≡ 1 (mod p−1)
那么我们有
dp * e = 1 + k(p−1)
又因为dp<p−1,根据平衡原则,所以有k<e,则我们可以在[1,e)的范围遍历k,找到满足等式的整数解,即可解出p。
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 79201858340517902370077926747686673001645933420450220163567700296597652438275339093680329918615445030212417351430952656177171126427547284822789947152085534939195866096891005587613262293569611913019639653984932469691636338705418303482885987114085769045348074530172292982433373154900841135911548332400167290083
c = 70109332985937768446301118795636999352761371683181615470371772202170324747707233792154935611826981798791499937601162039878070094663516868746240133223110650205575807753345252087103328657073552992431511929172241702073381723302143955977662087561904058172777520360991685289300855900793806183473523998422682944404
dp = 3098334089252415941833934532457314870210700261428241562420857845879512952043729097866485406309479489101668423603305497982177150304625615059119312238777275
e = 65537
for k in range(1, e):
if (e * dp - 1) % k == 0:
p = (e * dp - 1) // k + 1
if n % p == 0:
q = n // p
d = invert(e, (p - 1) * (q - 1))
m = powmod(c, d, n)
break
print(long_to_bytes(m))
#NSSCTF{just_dp_leak}[RSA2]P11(e很大的dp泄露攻击)
题目
from Crypto.Util.number import *
flag = b'NSSCTF{******}' + b'1'*80
p = getPrime(512)
q = getPrime(512)
n = p*q
e = getPrime(128)
d = inverse(e, (p-1)*(q-1))
dp = d % (p-1)
m = bytes_to_long(flag)
c = pow(m, e, n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
print(f'dp = {dp}')
'''
n = 108280026722298796068968170303156759745471686664814404724171434502249429011870583595808692893118419248225924869164875379709992190884930717654004006466664403479467573176438601715156464950045121937338569942817256182277141174728470067308962244296992229214749863655518517510026063088263849891990324547823192559069
e = 305691242207901867366357529364270390903
c = 26537258289122728220745496185201994733321402056894636636642710319261241111675937946139938310952968353253866895253865273981912174303818938005932883052177988834834575591342856235464380238486868448329727891268391728758132913642966389278296932186703733187105516710825918064228397602264185334108934765627411913661
dp = 2656631506624565349527023729530989647164022271235521672257622068579788839123502046687139927161669209201953909023994372208117081512139181611949631467292513
'''我的解答:
❤ 本题为e很大的dp泄露攻击例题
在上一题中我们发现dp泄露时可以利用dp和其他因子的关系式进行进一步推导,最终再分析未知数是否可解
dp * e = 1 + k(p−1)
上一题中最后我们发现未知数k是一个小于e的数,所以我们采用了遍历[1,e)的方式来进行爆破,但这种方法不总是可行,例如在本题中e是128位的素数,显然我们不能去爆破它了。
❤ 中间顺带一提,其实很多比赛题目可能会有V1、V2、V3…版本,实际上他们都是可以通过同样的信息来进行推导,本题可以看作是P10的升级版,不能用相同的方式则说明我们忽略了一些条件,而这些条件恰恰能够让我们完成解题所需的约束。在CTF的密码学中,如果卡题了,不妨此时静下来,再将所有得到的式子以及已知的条件罗列出来,一一进行排列推导可能得到的结果。(因为出题人也是这么出题的)
❤ 在RSA中,我们不仅有P10中e*dp的关系,还有其他我们可以利用的条件,由欧拉降幂有
ae*dp ≡ ae*dp mod p−1 ≡ a (mod p)
显然则说明ae*dp − a ≡ 0 (mod p)
所以有(ae*dp−a)∣p,显然我们已经攻破了本题,接下来我们需要求解和n的最大公因数即可。
当然这里需要注意我们还是有概率失败,一是要保证选取的素数与p互素,这很简单,如果不互素则等于我们已经得到了p的倍数了。二是可能结果得到了一个n的倍数,这样最大公因数将会是n,此时我们只需要重新选择a直至得到想要的结果即可。
❤ 显然我们会发现此法还需要一个存在条件便是e*dp>p−1,因为如果不满足将不能那样使用欧拉降幂,详见欧拉降幂的定义。所以本方法一般e都比较大,如果不满足则e很小用P10方法即可(这里还存在dp很小的可能,这种情况我们之后会继续讨论)
exp:
from Crypto.Util.number import *
from gmpy2 import *
n = 108280026722298796068968170303156759745471686664814404724171434502249429011870583595808692893118419248225924869164875379709992190884930717654004006466664403479467573176438601715156464950045121937338569942817256182277141174728470067308962244296992229214749863655518517510026063088263849891990324547823192559069
e = 305691242207901867366357529364270390903
c = 26537258289122728220745496185201994733321402056894636636642710319261241111675937946139938310952968353253866895253865273981912174303818938005932883052177988834834575591342856235464380238486868448329727891268391728758132913642966389278296932186703733187105516710825918064228397602264185334108934765627411913661
dp = 2656631506624565349527023729530989647164022271235521672257622068579788839123502046687139927161669209201953909023994372208117081512139181611949631467292513
m = getPrime(128) #这里要求m要与p互素,因此我们使用getPrime获取一个素数即可,位数不太大就好。
p = gcd(powmod(m, e*dp, n) - m, n)
q = n // p
d = invert(e, (p - 1) * (q - 1))
m = powmod(c, d, n)
print(long_to_bytes(m))
#NSSCTF{p_leak_but_with_huge_e}[RSA2]P12(d泄露攻击)
题目
from Crypto.Util.number import *
from gmpy2 import *
p = getPrime(512)
q = getPrime(512)
assert p < q
n = p*q
e = 65537
phi = (p-1)*(q-1)
d = invert(e, phi)
print(f'n = {n}')
print(f'd = {d}')
print('flag is NSSCTF{md5(p)}')
'''
n = 113917408220469425995764932761465306974540330325378601642830241920567032775895088098706711486764203845425248022960733155994427766750033219106642310531864450654102562104771892268897793145789045570107312401570269581223945259704851104645493075550316424129401227653740942495625720165869565257394427181127734628103
d = 15762135247924329080208071933121250646888501386858311483546464344350547831176536290630826247188272280853810047335214127264865205744683174860903496832368687060941437002920094364116706593296591581117381565805322046922482804679245558495134876677733584718947309975077159564300049936769192724856722338627154192353
flag is NSSCTF{md5(p)}
'''我的解答:
❤ 本题为d泄露攻击例题
本题我们的目标不再是求解明文,而是考虑当私钥已经泄露的情况,能否利用公私钥来进行因数分解。
首先,我们先将涉及公私钥的关系式列出,我们有
ed−1 = kφ(n)
同时我们还有
aed−1 ≡ 1(mod n)
我们不妨设ed−1=2st,使得t是一个奇数,这样我们遍历i∈[1,s],假设能够找到满足下列关系式的式子
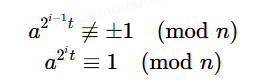
那gcd(a(2**(i−1))*t−1,n)便是n的一个非平凡因子,原式得解。
❤ 这里其实大家会看的很迷糊,为什么得到上述关系式就能说明
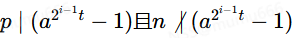
呢?这里我们要引入一个新定理
❤ 如果r≡s(mod ϕ(n)),则对于任意整数a都有ar≡as(mod n),也就是说我们可以将模n的同余幂式转换成其指数部分模ϕ(n)下的同余式。其中ϕ(n)=φ(n)/g,g=gcd(p−1,q−1)。
此时我们再回头来看本题证明就会清晰很多了

则说明2it ≡ 0(mod ϕ(n)),有
2i−1t = 2−1kϕ(n)
当k为奇数时,我们可以把式子先转换为
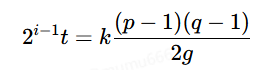
由欧拉准则有
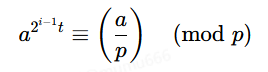
此时我们构造一个a使得满足为p的二次剩余则有
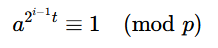
即
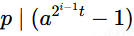
得证!
当k为偶数时,令k=2k1,显然有
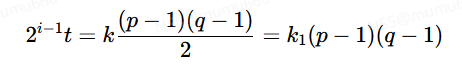
显然,虽然这个数是p−1的倍数,但还是(p−1)(q−1)的倍数,则
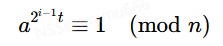
不符合要求。
❤ 实际上,在原文中只说明了存在一半的a都满足情况,但没有给出具体的证明。故这里我们也只证明到此处为止。
exp:
from Crypto.Util.number import *
from gmpy2 import *
import hashlib
n = 113917408220469425995764932761465306974540330325378601642830241920567032775895088098706711486764203845425248022960733155994427766750033219106642310531864450654102562104771892268897793145789045570107312401570269581223945259704851104645493075550316424129401227653740942495625720165869565257394427181127734628103
d = 15762135247924329080208071933121250646888501386858311483546464344350547831176536290630826247188272280853810047335214127264865205744683174860903496832368687060941437002920094364116706593296591581117381565805322046922482804679245558495134876677733584718947309975077159564300049936769192724856722338627154192353
e = 65537
t = e*d - 1
s = 0
while t % 2 == 0:
s += 1
t //= 2
found = False
for i in range(1, s):
c1 = powmod(2, powmod(2, i-1, n)*t, n)
c2 = powmod(2, powmod(2, i, n)*t, n)
if c1 != 1 and c1 != (-1 % n) and c2 == 1:
p = gcd(c1 - 1, n)
q = n // p
break
if p > q:
p, q = q, p
print('NSSCTF{%s}' % hashlib.md5(str(p).encode()).hexdigest())
#NSSCTF{f56299b1e5339dfebe8ea3d32dd44043}

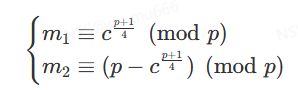



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· .NET10 - 预览版1新功能体验(一)