RSA入门（一）

一、RSA原理介绍(可结合本地视频学习)

非对称加密

💌 RSA加密算法其实是一种非对称加密算法，在各种场景与环境下都有它的身影，那么它和其它加密算法又有什么不同呢，以及什么是非对称加密算法？

💌 非对称加密：传统的加密算法是基于同一密钥进行加密和解密的，此时我们会发现我们攻击的重点将落在通信双方的密钥到底是什么，因为即使你的加密算法天衣无缝，但是你的密钥泄露了，我们便可以直接通过解密算法得到密钥。

通常在一个不安全的通信环境中，你的信息需要经过很多节点（中间人）才能传输至目标，此时我们考虑两个问题：

1. 如何保证我们发送的信息没有被中间人窃取？
2. 如何保证是可信的发送人（即别人不能伪造你的身份发送信息）？

其实这便是信息安全等级保护中的CIA三要素的机密性（Confidentiality）和完整性（Integrity）要求。

显然，依靠传统的对称密码我们没办法做到这两点，因为传统对称密码需要事先约定使用某个特定的密码进行通信。此时我们考虑这样一个加密算法，它拥有两组密钥。

公开密钥Pk（Public key）：又称公钥，可以公开给所有人进行存储。

私有密钥Sk（Secret key）：又称私钥，只能是发送者自己保存。

💌 如果我们规定加密时使用公钥，解密时使用私钥，那么似乎我们的第一个问题中的放窃取便有了解决方案。即别人就窃取不了了，因为他没有私钥。

假如我Kicky_Mu要给TagLmt发送信息，此时我只需要获取TagLmt的公开密钥（因为此密钥会公开给所有人），然后用这个公钥将我们的信息进行加密，再发送给TagLmt即可，TagLmt收到信息后只需要用自己的私钥解密即可。

这是为什么？

考虑到此时有一个中间节点（即中间人）获取了我们发送的信息，但是他只能得到加密的信息，而解密则需要私钥，他得不到私钥，因此他无法窃取我们的消息。

💌 那么如何保证可信呢，这里其实属于数字签名的内容，在后续的笔记中我们会详细介绍各类签名、认证算法，在这里我们可以稍作提及暂时不深究，其实我们只需要使用私钥对数据进行签名，用公钥进行验签即可。

RSA

💌 在刚才的讲解内容中，我们提到了非常多的新名词：

公钥、私钥、非对称、签名等等…

但我们如何实现这种算法呢，让我们回到本节内容的重点——RSA算法上，RSA 是 1977 年由罗纳德 · 李维斯特（Ron Rivest）、阿迪 · 萨莫尔（Adi Shamir）和伦纳德 · 阿德曼（Leonard Adleman）一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。

可以说整个密码学的基石都是基于一些数学难题，以RSA算法为例，其基于大整数分解难题（IFP），目前来说我们并没有什么有效的办法对一个极大整数做因式分解，再多的优化在极大整数面前都与爆破无异，这保障了RSA的安全性。

接下来我们来详细讲解RSA是如何工作的。

生成公私钥

1、首先选取两个不同的大素数 p和q，然后计算 N = p * q

2、求欧拉函数值 φ(N) = φ(p) * φ(q) = (p-1) * (q-1)

3、选择一个小于 φ(N) 的整数 e，并且满足 e 和 φ(N) 互质，求得 e 在模 φ(N) 意义下的乘法逆元 d，有 e * d ≡ 1 (mod φ(N))

$4、销毁\; p\; 和\; q$

此时有 (N,e) 为公钥， (N,d) 为私钥。

到这个地方可能此时的你已经懵了，不过没关系，我们来一一拆分解释，值得注意的是，你会发现不同的资料上的表述可能都不太一样，例如“素”和“质”的区分，实际上，这些内容在目前我们无须深究，所以只需要了解其含义即可，再之后的教程中我们会学习各类算法在不同环、域上的扩展，此时我们再来深究其数学意义。

💌 互质：两个正整数只有一个公因数1时，则称其为互质。比如：6和7互质，而4和6不互质。

💌 欧拉函数 φ(N) ：小于或等于 N 的正整数中与 N 互质的数的数目。例如：N = 6 那么此数目为2,φ(6) = 2*3=(2-1)*(3-1)=2 这里为什么不是1*6呢？因为2和3是两个素数。

若 p 为素数，则 φ(p) = p-1 (因为每一个小于p的数（这里指与p互质的小于p的那些数）都与p互质)

又有若 N = p * q，则 φ(N) = φ(p) * φ(q)，这里涉及到欧拉函数性质和计算方式，我们不在此深究，感兴趣的可以从N中有哪些和N不互质的数来进行推导本公式。

由此在RSA中，有φ(N) = (p-1) * (q-1)

💌 乘法逆元：

在加法中，我们有a+(−a)=0，我们称其互为相反数。
在乘法中，我们有a⋅(1/a)=1，我们称其互为倒数。
在矩阵中，我们有M⋅M⁻¹=E，我们称其为逆矩阵。

其实我们可以用一个统一的称呼：逆元，即某种运算下的逆元素，我们会发现，元素和其逆元素进行运算之后总是一个定值，实际上在代数中，他们构成了一个群（不用深究），我们只需要了解是在模意义下的乘法逆元即可。

在模 p 意义下，指的是后续的所有运算都是在模 p 的条件下满足，例如 3⋅4≠1

但 (3⋅4) mod 11=(1) mod 11，对于这种式子我们称其为同余式，并且有专门的同余符号进行表示：

$$3\cdot 4\equiv 1(\mathrm{mod}11)$$

$$所以参考上面乘法中的逆元运算规则，在模意义下则有：$$

                  a⋅a⁻¹ ≡ 1(mod p)

我们称 a 和 a⁻¹ 互为在模 p 意义下的乘法逆元。例如上述中的 3 与 4 互为在模 11 下的乘法逆元。

💌 至此你应该能够理解上述内容中的各项式子代表的意义了，那么如何用这些数字来进行加解密呢，我们继续往下讲解。

RSA加密解密

加密

$$💌$$ RSA算法本质上都是基于数学运算，在加密时我们需要先将消息转化为一个数字 m（例如消息ASCII码的二进制排列转为数字），然后有

$$c\equiv m{}^e(\mathrm{mod}N)$$

此时得到的 c 便是我们的密文。

解密

$$💌$$ 加密时我们只用到了公钥 (N,e)，同理解密时我们也只需用到私钥 (N,d)。有：$$m\equiv c{}^d(\mathrm{mod}N)$$

此时得到的 m 便是我们的明文消息。

正确性证明

$$💌$$ 也许此时你不明白为什么 m 能经过不同的两次幂运算后会得到原始值，这其实就是为什么RSA中要用到欧拉函数，如果你还不能够理解上面的一切，下面的正确性证明可以先略过，不要给自己徒增压力

转换为证明

m ​≡ c^d ≡ (m^e)^d ≡ m^ed(mod N)  （在模相同情况下，同余式是可以如此转换的）

​又有 ed ≡ 1(mod φ(N))，即ed = 1 + kφ(N)。

1、若gcd(m,N) = 1，则m^ed ≡ m^ed−1⋅m ≡ m^kφ(N)⋅m ≡ m (mod N)。原始得证。（中间涉及到欧拉定理 a^φ(n)≡1(mod n)）

2、若gcd(m,N) ≠ 1，则 m 为 p 或 q 的整数，设 m = hp，有

$$\begin{array}{l}m{}^{ed}\end{array}$$

其中

m^{k(p−1)(q−1)} = (m^k(p−1))^q−1 = 1 + xq​

原式得证。

$$💌$$ 至此，我们用尽可能用简洁的内容将RSA的原理与作用简单描述了一遍，接下来我们便开始正式进入CTF中的RSA算法学习了。

二、RSA算法实现(可结合本地视频学习)

$$💌$$ 再上一节中我们学习了RSA的数学原理基础，本节我们将了解如何具体实现RSA算法。

注意，在大部分资料中，其他作者更喜欢使用举一些特定的数字带入运算，从而让读者明白整个流程或从数字上直观的得到不同算式之间的联系。但我不会在这里不会使用此方式来阐述RSA的算法流程，带入具体数值进行计算观察关系的方式在解题时非常有效，但更多的我希望大家能够理解一种抽象的思维，这对我们后续的学习非常有帮助，当然大家在学习过程中可以自行选择自己喜欢的方式进行操作。

我们使用Python语言来实现一个RSA算法，首先你需要确保你已经安装好了Python执行环境以及编辑环境。（这一步如果有问题请自行搜索解决）

我使用的环境为Python 3.9.12 + VSCode（强烈推荐此环境），当然也并不需要和我的环境保持一致，可以选择自己熟悉或喜爱的环境进行操作，不过Python请使用3.8及以上版本，不然某些操作可能会得到不一样的结果。

这里默认大家已经基本掌握了Python语法，我将只会解释代码中新出现的库、函数、类的用法和说明。

Python实现RSA

$$💌$$ 上一节我们发现RSA无外乎就是那几个参数之间的运算，而我们要做的便是使用Python实现这些算式，首先我们要做的第一步是

1、生成两个大素数P、Q

这是一个很模糊的概念，希望各位在学习中能够做到尽量严谨，很显然，这里定义的大素数到底多大才是大呢？

10算大吗？100算吗？10000算吗？葛立恒数算吗？

我们需要一个更加精确的说法，我们生成两个512位的素数（这里包括之后的内容中涉及到的位都是指二进制位而不是十进制），那么如何使用Python产生一个素数呢，如果不借助任何外力的情况，我们可以从1开始选择，2，3，4…直到某个数满足512位且为素数为止，但是既然我们都使用Python了，为何还要这样做呢？

让我们来使用Python强大的开源库pycryptodome，安装命令如下：

pip3 install pycryptodome
# 或
python3 -m pip install pycryptodome

如果有路径报错问题，使用命令

pip install --target=路径（这里的路径不用担心，报错的时候系统会给出你路径的，只需要复制过来即可） pycryptodome

如果还报错而且提示你需要更新那么使用命令

pip install --upgrade --target=上面一样的路径 模块名

按上述操作便可以成功安装，然后在Python环境中执行以下代码

import Crypto

如果没有显示ModuleNotFoundError：等诸如此类的错误的话，那么恭喜你成功的安装了本库。这里你可能会奇怪为什么安装使用pycryptodome，而引入时使用Crypto，这涉及到这的库和其他库的一些联系，有兴趣的可以自行去查找。

然后我们就可以生成素数了，我们引入库中的子包Crypto.Util.number，这个子包中包含了大量的数学工具，之后我们会经常用到这个子包。

from Crypto.Util.number import *
p = getPrime(512)
q = getPrime(512)
print(p)
print(q)

执行上面的代码，你便可以得到两个512位的素数，这依赖于我们调用了包中的getPrime函数，它能够返回一个n位的素数，其中n是我们的传入参数。至此我们便完成了RSA的第一步。

2、$n=p\cdot q,\phi (n)=(p-1)(q-1)$

$后续的过程便简单了很多，我们只需要在之前的基础上完成运算即可，添加下列代码并执行$

n = p*q
phi = (p-1)*(q-1)

3、选取与φ(n)互素的$e$，计算满足ed ≡ 1(mod φ(n))

这里我们要完成两个数学操作，一个是互素的判断，一个是求解e的乘法逆元。代码如下：

e = 65537
assert GCD(e, phi) == 1, "判断互素"
d = inverse(e, phi)

这里GCD函数能够求解最大公因数（Greatest Common Divisor），之前我们学习了互素的概念就是两个数的最大公因数为1，所以这里我们用断言表达式认定e一定是和phi互素的。为什么我们要选择65537作为e呢，实际上这并不是硬性规定，一些标准提供了一些e的参考值，65537在各类实现与标准中被广泛使用，但是这并不影响你可以将值改变为其他值进行后续的操作。
求解d的过程中，我们使用了inverse函数，该函数有两个参数(a,p)，作用便是求解a在模p意义下的乘法逆元，那么这里我们便是求解e在模phi下面的乘法逆元，结果为d。之前我们提到了逆元是互为逆元，所以你可以尝试下面的代码

print(inverse(d, phi) == e)

打印的结果将为True，从这里我们也可以看出在RSA中的关键点便是获取这个phi的值，因为得到了phi我们便可以求e或d的值，而这正是我们加解密的密钥参数。

4、$(n,e)$即为公钥，(n,d)即为私钥，此时我们便得到了一组RSA的公私钥，随后我们便可以开始用这组密钥来进行加解密操作。

加密：

假设我们要加密的消息为Hello，我们定义一个字符串进行存储

message = b'hello'

注意这里我们定义的是一个bytes类型字符串，它将每个字符用8位二进制进行存储，是字符串最原生的存储形式。你也可以直接定义'hello'，但在Python3中它是一个Unicode的字符串，需要进行编码操作才能转换为bytes类型进行后续的运算。

但我们在RSA中是数与数的运算，该如何将字符串参与操作呢？

我们使用包中的bytes_to_long函数，从函数名也可以猜出来，这个函数是将字符串转换为数字，运行下列代码

m = bytes_to_long(message)
print(m)

此时，我们的消息已经被转换为一个字符串了。随后我们便可以对消息进行RSA加密

c = pow(m, e, n)
print(c)

我们使用Python自带的pow函数进行幂运算，注意不要写成m ** e % n，二者代表的意义相同，但是pow函数内置快速幂，可以快速得出结果，而m ** e % n会将m^e的结果先计算出来再取模，m^e是一个非常大的数，这会消耗你计算机大量的运算和存储资源。

至此，我们便完成了加密过程，得到了RSA的密文C。

解密：

我们执行代码：

msg = pow(c, d, n)
print(msg)

此时我们便完成了RSA的解密操作，随后你可以比较一下msg和m的值，他们会是一样的。

$$💌$$ 完整代码：

from Crypto.Util.number import *
p = getPrime(512)
q = getPrime(512)

n = p*q
phi = (p-1)*(q-1)
e = 65537
assert GCD(e, phi) == 1, "判断互素"
d = inverse(e, phi)

print(f'公钥：({e}, {n})')
print(f'私钥：({d}, {n})')

message = b'hello'
m = bytes_to_long(message)
print('消息：', m)

c = pow(m, e, n)
print('密文：', c)

msg = pow(c, d, n)
print('明文：', msg)

assert msg == m, "是否一样"

三、欧拉函数及其性质(可结合本地视频学习)

之前的内容我们对于欧拉函数没有做详细的介绍，因为重点是先理解RSA的算法过程，但要想深入学习密码学各个攻击的原理，我们必须掌握欧拉函数及其性质，本篇将介绍欧拉函数涉及的数学定理以及运算。

欧拉函数计算

$$💌$$ 之前我们已经介绍过欧拉函数的定义了

$\phi (n)$为在小于n的正整数中与n互素的数的数目。

此前我们只讨论了特殊的情况，当p为素数时，有φ(p)=p−1，现在我们来讨论更一般的情况，当n是一个双因子合数时

$$n=p\cdot q$$

我们考虑和n不互素的数有

$$p,2p,3p,\cdots ,(q-1)p,q,2q,3q,\cdots ,(p-1)q$$

因为只有这些数和n的最大公因数不为1，则欧拉函数值应该为n−1减去这些不互素的数的数目

$$\phi (n)=(pq-1)-(q-1)-(p-1)=(p-1)(q-1)$$

$$显然对于三个因子，多个因子我们都可以得到上面的结论，即当$$

$$n=p^1{p}^2\cdots p{}^r$$

有

$${}^1$$

💌 现在我们考虑因子阶不为1的情况，还是先从双因子数讨论

n = p^k1​q^k2​

此时，和n不互素的数有

p,2p,⋯,(q^k2​−1)p,q,2q,⋯,(p^k1​−1)q

$$但我们会发现，上面的数中又可能会存在重复的数，例如$$

$$p,2p,\cdots ,qp,\cdots ,2qp,\cdots ,(q^{2}p{}^1-1)p$$

$$q,2q,\cdots ,pq,\cdots ,2pq,\cdots ,(p^{1}q{}^2-1)q$$

显然这里的pq,2pq是同一个数，那有多少个重复的数呢，因为p前面系数最大为q^k2p^k1−1−1，所以应该会出现⌊(q^k2p^k1−1−1)/q⌋ = q^k2−1p^k1−1−1个带有$q$的值，同理另一边会有⌊(p^k1q^k2−1−1)/p⌋ = p^k1−1q^k2−1−1个带有p的值，显然这两个数一致，则有p^k1−1q^k2−1−1个重复的值

φ(n) ​= (q^k2​p^k1​−1)−(q^k2​p^k1​−1−1)−(p^k1​q^k2​−1−1)+(p^k1​−1q^k2​−1−1)

= q^k2​(p^k1​−p^k1​−1)+q^k2​−1(p^k1​−1−p^k1​)

= q^k2​−1(q(p^k1​−p^k1​−1)−(p^k1​−p^k1​−1))

= q^k2​−1(p^k1​−p^k1​−1)(q−1)

= q^k2​−1(q−1)⋅p^k1​−1(p−1)

同样的方法我们可以得到任意的

n = p₁^k1​​p₂^k2​​⋯p_r^kr​​​

有

φ(n) = p^k1​−1(p−1)⋯p_r^kr​−1​ = ∏_i=1​^r p_i^ki​−1​(p_i​−1)

其实这里推多阶我们还可以用另一个思路考虑，我们考虑每个因子p来带的互素系数的个数，也就是上面的每一个与n不互素的数其实都是这些系数的排列组合，例如一阶时的

$$p,2p,3p,\cdots ,(q-1)p,q,2q,3q,\cdots ,(p-1)q$$

其实是p−1个系数和q−1个因子的组合，同理二阶中不互素的数我们转换为

$$1\cdot n/p^1,2\cdot n/p^1,\cdots ,p{}^1(p-1)\cdot n/p^1$$

$$1\cdot n/q^2,2\cdot n/q^2,\cdots ,q{}^2(q-1)\cdot n/q^2$$

为什么？因为我们把n/p^k1​看作一个整体，这个数是和n不互素的一个数（因为有其他因子），这个整体乘上其他系数也一定不互素，最多有多少个系数呢？有p^k1−1(p−1)个（再加1乘上去就是n了）。

所以其实从系数排列组合的角度我们还可以同样的结论，得到对于

n = p₁^k1p₂^k2⋯p_r^kr​​

有

φ(n) = ∏_i=1^r p_i^ki−1(p_i−1)

这个式子很重要，我们一定要记得欧拉函数值该怎么求。

欧拉函数性质

💌 欧拉函数在数论中有广泛的运用，在此我们并不会讨论完所有关于欧拉函数的性质，只会重点讲解一些于CTF中涉及的性质。

1、积性函数

积性函数：对于任意互质的整数 a和b有性质f (ab)=f (a)f (b)的 数论函数 。
完全积性函数：对于任意整数 a和b有性质f (ab)=f (a)f (b)的 数论函数 。

显然欧拉函数属于积性函数，因为其值来自每一个因子的乘积，而每个系数刚好又是每个因子的欧拉值，即

φ(p^k1q^k2) = φ(p^k1)φ(q^k2)

这个性质可以推广到r个因子中，即

φ(n) = φ(p₁^k1)φ(p₂^k2)⋯φ(p_r^kr)

2、欧拉定理

若(a,m)=1（我们一般用(a,b)代表gcd⁡(a,b)），则有a^φ(m)≡1(mod m)。

欧拉定理我们可以用如下思路证明，设小于m中与m不互素的数集为

s={x₁,x₂,⋯ ,x_φ(m)}

他们中任意两个值都满足（因为值本身不相等）

又a与m互素，我们可知有

(ax_i,m) = 1

因为他们中间不包含任何除1以外的公因子，那么此时我们有

ax_i ≡ x_j(mod m), (x_i,x_j∈s)

什么意思呢？就是说ax_i​模m的余数（设为r）r一定在集合s中，这里大家应该能理解，因为s中是所有小于m且和m互素的数，又r也和m互素，所以$r$一定在s中。并且我们还可以证明

ax_i ax_j(mod m)

这里可以用反证法，如果他们同余，则说明a(x_i−x_j)≡0(mod m)，说明a∣m或者(x_i−x_j)∣m，（a∣b代表a整除b）而这显然是和互素矛盾的。

进一步我们可以得到

x₁x₂⋯x_φ(m) ≡ ax₁⋅ax₂⋯ax_φ(m)(mod m)

这又是为何，因为我们不需要关心ax_i​的余数到底是哪个x_j​，我们只需要知道a和不同的x_i​得到的余数各不相同即可，那么φ(m)个相乘也会得到不同的φ(m)个值，也就是覆盖了集合s。

两边消项，有

1 ≡ a^φ(m)(mod m)

3、扩展欧拉定理

我们也称其为欧拉降幂，指的是

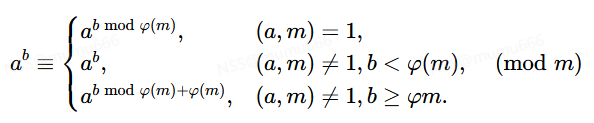
即我们可以将幂指数模φ(m)后处理。这里证明就不细说了。证明可参考：扩展欧拉定理

四、模的性质(可结合本地视频学习)

💌 在之前的内容中我们介绍了同余的概念，关于模运算后面会经常出现在我们的题目中，因为取模本质是一种信息丢失，所以使得正向运算非常简单，我们很容易计算一个值取模后的结果，但却很难从余数中恢复这个数的原始值，所以取模经常出现在密码学的运用之中。

性质

1、同余

若a mod p = b mod p，则称a与b在模p意义下同余，记作：

a ≡ b(mod p)

2、对称性

$$a\equiv b(\mathrm{mod}p)$$

3、传递性

若a ≡ b(mod p)且b ≡ c(mod p)，则a ≡ c(mod p)

4、结合律

$$((a+b)\mathrm{mod}p+c)\mathrm{mod}p=(a+(b+c)\mathrm{mod}p)\mathrm{mod}p$$

5、交换律

$$(a+b)\mathrm{mod}p=(b+a)\mathrm{mod}p$$

6、分配律

$$(((a+b)\mathrm{mod}p)\cdot c)\mathrm{mod}p=(ac\mathrm{mod}p+bc\mathrm{mod}p)\mathrm{mod}p$$

💌 同时取模运算和四则运算类似，有一点例外是除法，你会发现我们所涉及的所有数都是正整数，我们不关心分数和负数，在整数模运算中，除一个数应该写（说）成乘上该数的逆元素。

💌 在同余的情况下中，你可以将所有的操作都看作是整数的四则运算，不用关心运算过程中的取模，同理在做题时，如果涉及到要自己推式子，都可以按此操作，只需要记得最后取模即可。

💌 至此，RSA入门（一）的内容讲解到此结束！下面来练习一下例题吧！

五、例题

[RSA1]P1(签到)

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
phi = (p-1)*(q-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 10554915510546378513140074459658086644656654144905337809416976066414771647836950941616441505897207397834928781511863699153349798682451297889979721668885951
q = 8246403321715011123191410826902524505032643184038566851264109473851746507405534573077909160292816825514872584170252311902322051822644609979417178306809223
e = 65537
c = 40005881669517895877352756665523238535105922590962714344556374248977905431683140065629966778249773228248201807844489945346731806741025157651474530811920115794270396320935022110691338083709019538562205165553541077855422953438117902279834449006455379382431883650004540282758907332683496655914597029545677184720
'''

我的解答：

最基础的RSA，参数都给你了，直接梭

本题我们的关键是要得到phi，而题目则直接将p和q打印了出来，因此我们可以直接得到phi，从而求解逆元得到私钥d，然后解密原消息，得到flag

exp:

from Crypto.Util.number import *
p = 10554915510546378513140074459658086644656654144905337809416976066414771647836950941616441505897207397834928781511863699153349798682451297889979721668885951
q = 8246403321715011123191410826902524505032643184038566851264109473851746507405534573077909160292816825514872584170252311902322051822644609979417178306809223
e = 65537
c = 40005881669517895877352756665523238535105922590962714344556374248977905431683140065629966778249773228248201807844489945346731806741025157651474530811920115794270396320935022110691338083709019538562205165553541077855422953438117902279834449006455379382431883650004540282758907332683496655914597029545677184720

n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)

print(long_to_bytes(m))
#NSSCTF{now!you_know_rsa}

注意flag是一个字符串，而我们解密得到的是数字，我们需要使用包中的long_to_bytes函数将数字转化回字符串。

[RSA1]P2(大数分解1)

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(256)
q = getPrime(256)
n = p*q
e = 65537
phi = (p-1)*(q-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')

'''
n = 7382582015733895208810490097582153009797420348201515356767397357174775587237553842395468027650317457503579404097373070312978350435795210286224491315941881
e = 65537
c = 6511001389892474870028836129813814173158254564777610289284056550272120510686249909340499673868720839756059423749304765055919251717618117507007046973023557
'''

我的解答：

本题和上一题的代码几乎一样，但是本题没有告诉我们p和q的值，那我们如何得到phi呢？

当题目没有给出除了公钥之外的任何信息时，我们便考虑是否n可直接分解，因为n=p⋅q，若我们能够成功进行分解便可以求得phi从而得到私钥。

这里我们使用factordb来进行分解，该网站存储了大量的因数关系，我们将n提交至该网站，便可以得到结果

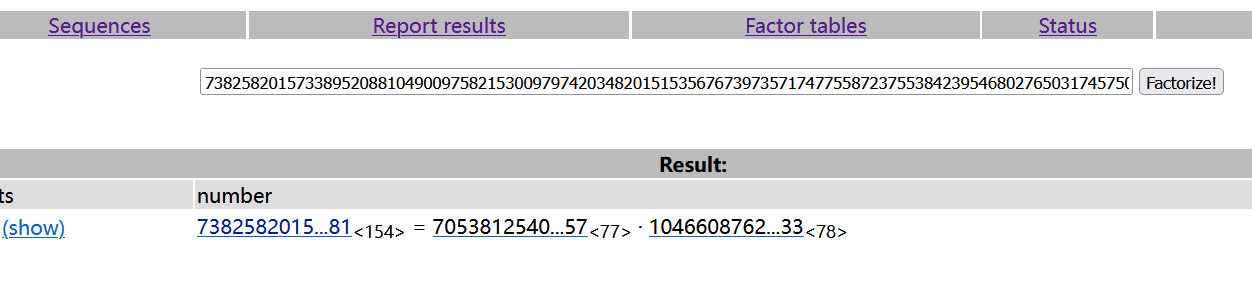
这样一来，我们成功将n分解成了两个因子，即p和q（谁是p谁是q的问题大部分情况下我们并不需要关注，即顺序无所谓）。然后便可以写出解密代码

exp:

from Crypto.Util.number import *
n = 7382582015733895208810490097582153009797420348201515356767397357174775587237553842395468027650317457503579404097373070312978350435795210286224491315941881
p = 70538125404512947763739093348083497980212021962975762144416432920656660487657
q = 104660876276442216612517835199819767034152013287345576481899196023866133215633
e = 65537
c = 6511001389892474870028836129813814173158254564777610289284056550272120510686249909340499673868720839756059423749304765055919251717618117507007046973023557

n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)

print(long_to_bytes(m))
#NSSCTF{factordb_is_useful}

[RSA1]P3(大数分解2)

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(128)
q = getPrime(128)
n = p*q
e = 65537
phi = (p-1)*(q-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')

'''
n = 53690629441472827148854210396580805205350972614395425306316047967905824330731
e = 65537
c = 22130296334673852790451396673112575082637108306697684532954477845025885087040
'''

我的解答：

跟上题代码一样，我们依然可以尝试使用factordb来分解本题中的n（依然可以分解）。然后写解码脚本即可。

不过这里我的本意不是让用factordb来分解的。那就顺便介绍另一种分解方法（对于这种不算太大的素数）：

有时候我们也会发现factordb分解并没有得到结果（大部分情况都是得不到的），此时我们观察题目，p和q是两个128位的素数，这个数相比之前我们生成的256或是512素数来说几乎是0（位数多一位，值增加两倍）。

对于这种不算太大的素数，我们可以尝试使用一些工具来分解这个数。

yafu便是这样一种工具，它内置了各种分解算法，能够对不太大或者一些特殊情况下的数进行因式分解。

下载地址：https://sourceforge.net/projects/yafu/

下载解压后目录下会有

yafu
yafu-Win32.exe
yafu-x64.exe

分别是yafu的linux、Windows32位和Windows64位版本。我们这里使用yafu-x64.exe进行操作。

我们在当前目录下进入终端（Windows下上方地址栏输入cmd回车即可进入终端）

输出yafu-x64.exe并按回车运行，然后输入factor(xxx)，xxx是你想分解的输入，例如对于本题

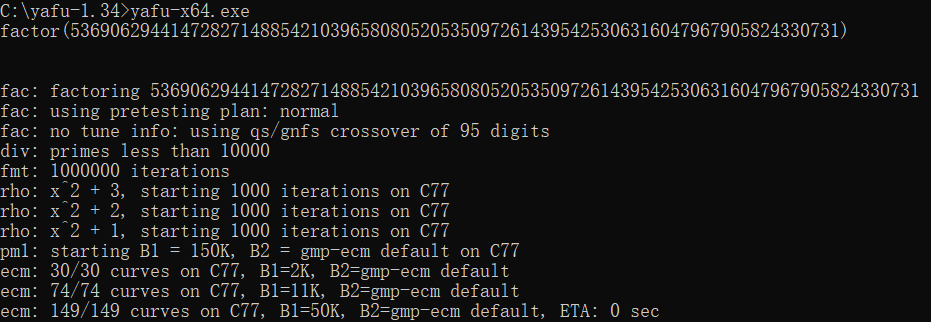
稍作等待，便可以得到分解结果

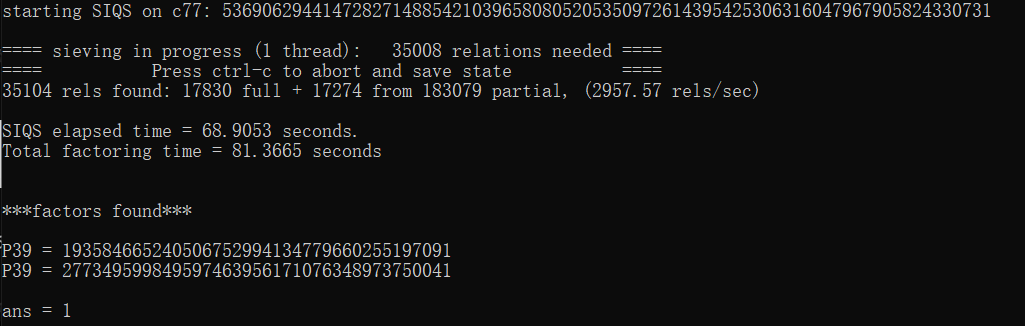
可以看到一共花费了81秒完成了对这个数的分解，上面的其他输出则是yafu采用的分解算法以及参数等内容。

得到了p和q的值我们便可以写出解密代码了。

exp:

from Crypto.Util.number import *
n = 53690629441472827148854210396580805205350972614395425306316047967905824330731
p = 193584665240506752994134779660255197091
q = 277349599849597463956171076348973750041
e = 65537
c = 22130296334673852790451396673112575082637108306697684532954477845025885087040

n=p*q
phi = (p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)

print(long_to_bytes(m))
#NSSCTF{yafu!yafu!yafu!}

[RSA1]P4(邻近素数)

题目

from Crypto.Util.number import *
import gmpy2
flag = b'NSSCTF{******}'

p = getPrime(512)
q = gmpy2.next_prime(p)
n = p*q
e = 65537
phi = (p-1)*(q-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')

'''
n = 115637000420176820831322601039129424406844427046456738651883381559357542765613732363445112111006849040385859313572091386802534464534403117787314180179562651607533039692795522388596550968316951090748054495960090527479954143448774136390568881020918710834542819900918984139672802889774720153267841255456602500057
e = 65537
c = 98161406745910866780822530171878255235776133393411573803496865047700715941955255328757920065032397556905095591171977170479344602512244671081108703687450560269408412671849929423399172588599903975793985819498354819305128607934552101433664794909855378636055525016664559476808490723554481335856183927702549281730
'''

我的解答：

本题包含了之前我们还没接触的另一个包gmpy2

该包默认编译版本为linux，故在Windows不要用pip直接安装

访问https://github.com/aleaxit/gmpy/releases下载相应版本，cp36代表Pythone3.6，x86代表Windows64位，其他同理。

下载完成后在文件目录下打开终端，输入pip3 install gmpy2-2.xx-cpxx-xxxxxx.whl，其中gmpy2-2.xx-xxx是你下载的完整文件名（这里切记就算文件名很长也不要修改文件名，也不要换路径），即可安装成功。

该库也是一个数学工具库，且底层使用C编写，执行效率相比Python实现会快很多。

题目生成了一个512位的素数p，随后使用next_prime函数获取p的下一个素数作为$q$，然后再做RSA算法，本题素数都比较大，我们没办法直接分解这个素数。但是我们发现$p$和$q$之间似乎有一些联系，它们太接近了，素数在自然数中其实没那么少，我们可以进行测试:

from Crypto.Util.number import *
import gmpy2
p = getPrime(512)
q = gmpy2.next_prime(p)
print(q-p)

你会发现大部分情况下二者的差值都小于1000，那么有这层关系我们如何解题呢。考虑$n$的算术平方根为sn=√n，同时sn也是p和q的几何平均值。此时则有

$$p<sn<q$$

我们又有q,p是相邻的素数，p的下一个素数为$q$，同理也有sn的下一个素数也应该是$q$，到这里你或许应该知道我们该怎么操作了。但是如何编写代码求平方根呢？这里我们借助gmpy2中的isqrt函数，在后续我们更多的会使用gmpy2而不是Crypto中的数学函数（因为二者速度不是一个量级）。

sn = isqrt(n)
q = next_prime(sn)
p = n // q

注意除的时候需要用整除。

exp:

from Crypto.Util.number import *
from gmpy2 import *
p = getPrime(512)
q = gmpy2.next_prime(p)

n = 115637000420176820831322601039129424406844427046456738651883381559357542765613732363445112111006849040385859313572091386802534464534403117787314180179562651607533039692795522388596550968316951090748054495960090527479954143448774136390568881020918710834542819900918984139672802889774720153267841255456602500057
e = 65537
c = 98161406745910866780822530171878255235776133393411573803496865047700715941955255328757920065032397556905095591171977170479344602512244671081108703687450560269408412671849929423399172588599903975793985819498354819305128607934552101433664794909855378636055525016664559476808490723554481335856183927702549281730

sn = isqrt(n)
q = next_prime(sn)
p = n // q

phi = (p-1)*(q-1)
d = invert(e, phi)

m = pow(c, d, n)
print(long_to_bytes(m))
#NSSCTF{so_closed}

[RSA1]P5(费马分解)

题目

from Crypto.Util.number import *
import gmpy2
flag = b'NSSCTF{******}'

p = getPrime(512)
q = gmpy2.next_prime(p - getPrime(256))
n = p*q
e = 65537
phi = (p-1)*(q-1)
m = bytes_to_long(flag)
c = pow(m, e, n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
'''
n = 148841588941490812589697505975986386226158446072049530534135525236572105309550985274214825612079495930267744452266230141871521931612761645600600201983605957650711248808703757693378777706453580124982526368706977258199152469200838211055230241296139605912607613807871432800586045262879581100319519318390454452117
e = 65537
c = 69038543593219231496623016705860610154255535760819426453485115089535439537440188692852514795648297200067103841434646958466720891016026061658602312900242658759575613625726750416539176437174502082858413122020981274672260498423684555063381678387696096811975800995242962853092582362805345713900308205654744774932
'''

我的解答：

题目生成了一个512位的素数p，随后使用next_prime函数获取p−r的下一个素数作为$q$，其中r为一个随机的256位素数，然后再做RSA算法，我们可以认为p和q依然是两个比较接近的数（因为r的大小在p和q面前不值一提），但如果想和上一题一样便不能了，因为当我们求解sn=√(n)后，q不再是sn相邻的素数，而是查找达到r，也就是说我们可以在r的范围内找到q，但对于我们来说256位是一个不小的数，我们显然不能一一开始遍历进行判断，在这种情况下，我们需要一种更加通用的算法：

费马分解： 有

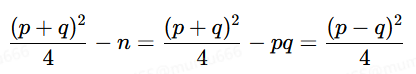
既然p−q比较小，则说明(p−q)²/4也比较小，则说明(p+q)²/4和n也差不多大，所以(p+q)/2应该和√n差不多大，那么我们可以

1、遍历大于√n​的每一个整数x，若满足x²−n为平方数，即x²−n=y²，则有x²=(p+q)²/4,y²=(p−q)²/4

2、解上述式子，即可得到p,q

通俗一点来说，当(p+q)/2和sn接近时，我们便可以用此方法分解n，那么如何判断是否接近呢？其实本质就是两个值的算术平均值和几何平均值，俩个值越接近，其二种平均值也越接近，所以当p和q比较接近时，我们便可以利用费马分解方法。

exp:

from Crypto.Util.number import *
from gmpy2 import *

def fermat_attack(n):
    a = isqrt(n)
    b2 = a*a - n
    b = isqrt(n)
    count = 0
    while b*b != b2:
        a = a + 1
        b2 = a*a - n
        b = isqrt(b2)
        count += 1
    p = a+b
    q = a-b
    assert n == p * q
    return p, q

n = 148841588941490812589697505975986386226158446072049530534135525236572105309550985274214825612079495930267744452266230141871521931612761645600600201983605957650711248808703757693378777706453580124982526368706977258199152469200838211055230241296139605912607613807871432800586045262879581100319519318390454452117
e = 65537
c = 69038543593219231496623016705860610154255535760819426453485115089535439537440188692852514795648297200067103841434646958466720891016026061658602312900242658759575613625726750416539176437174502082858413122020981274672260498423684555063381678387696096811975800995242962853092582362805345713900308205654744774932

p, q = fermat_attack(n)
phi = (p-1)*(q-1)
d = invert(e, phi)

m = pow(c, d, n)
print(long_to_bytes(m))
#NSSCTF{fermat_factor}

[RSA1]P6(共享素数)

题目

from Crypto.Util.number import *
flag = b'NSSCTF{******}'

p1 = getPrime(512)
q = getPrime(512)
p2 = getPrime(512)

n1 = p1*q
n2 = p2*q

e = 65537

m = bytes_to_long(flag)
c1 = pow(m, e, n1)
c2 = pow(m, e, n2)

print(f'n1 = {n1}')
print(f'n2 = {n2}')
print(f'e = {e}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
'''
n1 = 143348646254804947818644803938588739009782265465565896704788366218178523508874903492905378927641178487821742289009401873633609987818871281146199303052141439575438691652893995423962176259643151111739185844059243400387734688275416379337335777994990138009973618431459431410429980866760075387393812720247541406893
n2 = 138110854441015362783564250048191029327770295545362614687087481715680856350219966472039006526758450117969049316234863489558254565946242898336924686721846675826468588471046162610143748100096038583426519355288325214365299329095841907207926280081868726568947436076663762493891291276498567791697978693639037765169
e = 65537
c1 = 54957154834913405861345262613986460384513988240935244315981524013378872930144117440787175357956479768211180412158274730449811947349624843965933828130932856052315165316154486515277625404352272475136003785605985702495858150662789554694910771308456687676791434476722168247882078861234982509648037033827107552029
c2 = 122221335585005390437769701090707585780333874638519916373585594040154234166935881089609641995190534396533473702495240511296379249872039728112248708182969185010334637138777948970821974238214641235158623707766980447918480715835847907220219601467702961667091318910582445444058108454023108157805147341928089334736
'''

我的解答：

本题生成了三个素数p1,p2,q，且有n1=p1∗q,n2=p2∗q，我们可以看作是两组公钥（虽然他们使用了相同的e），然后用这两种公钥都对flag进行了RSA加密。

我们会发现n1和n2包含相同的因子q，即这是这二者的公因子，又因为n1,n2每个数都只有两个因子，则q还是二者的最大公因数，我们可以使用GCD或gmpy2包中的gcd函数进行求解。

当我们得到了q，便可以用整除n1,n2得到剩下的因子，但是因为二者都对flag进行了加密，我们只需要解密任意一个值即可，不过值得注意的是，若是使用n1的加密值，则需要用p1和q，以及取模时要模n1，不要混淆了各个数字。

exp:

from Crypto.Util.number import *
from gmpy2 import *

n1 = 143348646254804947818644803938588739009782265465565896704788366218178523508874903492905378927641178487821742289009401873633609987818871281146199303052141439575438691652893995423962176259643151111739185844059243400387734688275416379337335777994990138009973618431459431410429980866760075387393812720247541406893
n2 = 138110854441015362783564250048191029327770295545362614687087481715680856350219966472039006526758450117969049316234863489558254565946242898336924686721846675826468588471046162610143748100096038583426519355288325214365299329095841907207926280081868726568947436076663762493891291276498567791697978693639037765169
e = 65537
c1 = 54957154834913405861345262613986460384513988240935244315981524013378872930144117440787175357956479768211180412158274730449811947349624843965933828130932856052315165316154486515277625404352272475136003785605985702495858150662789554694910771308456687676791434476722168247882078861234982509648037033827107552029
c2 = 122221335585005390437769701090707585780333874638519916373585594040154234166935881089609641995190534396533473702495240511296379249872039728112248708182969185010334637138777948970821974238214641235158623707766980447918480715835847907220219601467702961667091318910582445444058108454023108157805147341928089334736

q = gcd(n1, n2)
p1 = n1 // q
phi = (p1-1)*(q-1)
d = invert(e, phi)

m = pow(c1, d, n1)
print(long_to_bytes(m))
#NSSCTF{no_share_number}

[RSA1]P7(多因子)

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}' + b'1'*170

p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
n = p*q*r
e = 65537
phi = (p-1)*(q-1)*(r-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'r = {r}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 10666139331774428325755287635566473140804481321882464031499529816800186578792308674238646794969384836340484775213796013129603472328582005363876462361316357
q = 8419311673449738061914489023962717718536471719688567807316495262754711350004888752049108347226115000749280146228195893953964759818878155006622123533942989
r = 12875078327453384158245832541544758526474680184252540739652077682353277702054275525591573258723948221345537075374635382175740236093131628077747126356403959
e = 65537
c = 424552463648937499189041230155623101311087334789253159440707211761796081289342164253743235182597460622581134089949035117444838205449163269030784233435435681797627188717450074808905561404960693227573181548281296514743775615606388692910356320667720308219275107443303501165027740512539959960217657836317351146520079753390346207659007421416917274795119021374032194294225350901136669304225010974617136606299060486198480556729770211945777266366417547752798441211059402
'''

我的解答：

本题为RSA一种变式情况，在本题中，n由三个素数因子构成，给出参数以及加密值，需要我们进行解密，在常规的RSA中有

$$\phi (n)=\phi (p)\phi (q)=(p-1)(q-1)$$

$$那么是否在本题中有$$

φ(n)=φ(p)φ(q)φ(r)=(p−1)(q−1)(r−1)

呢？答案是肯定的（前面的讲解中提到过），其实如果有

$$n=p^1{p}^2{p}^3...$$

$$我们还可以推广得到$$

φ(n)=φ(p_1​)φ(p₂​)φ(p₃​)...=(p₁​−1)(p₂​−1)(p₃​−1)...

至于为什么？请见前面对欧拉函数的介绍

exp:

from Crypto.Util.number import *

p = 10666139331774428325755287635566473140804481321882464031499529816800186578792308674238646794969384836340484775213796013129603472328582005363876462361316357
q = 8419311673449738061914489023962717718536471719688567807316495262754711350004888752049108347226115000749280146228195893953964759818878155006622123533942989
r = 12875078327453384158245832541544758526474680184252540739652077682353277702054275525591573258723948221345537075374635382175740236093131628077747126356403959
e = 65537
c = 424552463648937499189041230155623101311087334789253159440707211761796081289342164253743235182597460622581134089949035117444838205449163269030784233435435681797627188717450074808905561404960693227573181548281296514743775615606388692910356320667720308219275107443303501165027740512539959960217657836317351146520079753390346207659007421416917274795119021374032194294225350901136669304225010974617136606299060486198480556729770211945777266366417547752798441211059402

n=p*q*r
phi = (p-1)*(q-1)*(r-1)
d = inverse(e, phi)
m = pow(c, d, n)

print(long_to_bytes(m))
#NSSCTF{3th_number!}11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111

不过至于本题为何要添加上大量的字符1作为填充内容，这个问题待到P9时我们便会知晓。

[RSA1]P8(欧拉函数)

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}' + b'1'*100

p = getPrime(256)
q = getPrime(256)
n = (p**3) * q
e = 65537
phi = (p-1)*(q-1)

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 80505091208742938705306670241621545375764148093711243653439069254008824979403
q = 67599990875658931406915486208971556223245451500927259766683936131876689508521
e = 65537
c = 7958690969908064264211283192959937430539613460471121984649054121171267262097603091410178042319139582772142226087020110084551158367679146616732446561228522673699836019156243452069036383047309578614662564794584927846163157472211089368697387945469398750955336949678910159585015004994620777231073804301249774041
'''

我的解答：

本题为RSA一种变式情况，在本题中，n = p³q

是否在本题中有

φ(n)=φ(p³)φ(q)=(p−1)³(q−1)

呢？答案是否定的，这个式子只对了一半，φ(n)=φ(p³)φ(q)正确，但φ(p³)应该为p²(p−1)

可尝试自行对这个公式进行推导，详见前面对欧拉函数的介绍

exp:

from Crypto.Util.number import *

p = 80505091208742938705306670241621545375764148093711243653439069254008824979403
q = 67599990875658931406915486208971556223245451500927259766683936131876689508521
e = 65537
c = 7958690969908064264211283192959937430539613460471121984649054121171267262097603091410178042319139582772142226087020110084551158367679146616732446561228522673699836019156243452069036383047309578614662564794584927846163157472211089368697387945469398750955336949678910159585015004994620777231073804301249774041

n = (p**3)*q
phi = (p**2)*(p-1)*(q-1)
d = inverse(e, phi)
m = pow(c, d, n)

print(long_to_bytes(m))
#NSSCTF{more_exp}1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111

不过至于本题为何要添加上大量的字符1作为填充内容，这个问题待到P9时我们便会知晓。

[RSA1]P9(多因子变形)

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(512)
q = getPrime(512)

e = 65537
while True:
    r = 2*getPrime(100)*e+1
    if isPrime(r):
        break

n = p*q*r

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'r = {r}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 7478755670255767435237487693415479182290330775502792675052667363676831056436638619069277770540533350723045234676443621124912287506103439704868369839725279
q = 9232828888049557325429111621080998490274442347556398052322580869768941301413255711626092627273543579067597113958627672298942570149816938335701615759283713
r = 102909133680612532601801231903654039
e = 65537
c = 142893174944324070830219394465469685943669308818639857030565389839224452373848570577201378981080333784852764502832587008270072323948511579823852437852643609820245476634896477031076952735298279618952398460203032125853063235638358942643559551563899381032067185778629120272032518475352761100115057449043142848203976076694124978394099839339406197
'''

我的解答：

又是一道多因子的题目，不同的是此处的r = 2r_n⋅e + 1，这有什么特殊之处吗？

你可以尝试直接按照P7的exp来进行求解，会发现解出来的明文是乱码，或者你可以将代码中inverse函数替换为gmpy2中的invert函数（二者功能一样），你会发现得到了一个错误

ZeroDivisionError: invert() no inverse exists

提示逆元不存在，这是为什么，我们来看一下此时的phi是多少

$$phi=(p-1)(q-1)(r-1)=(p-1)(q-1)\cdot 2r^n\cdot e$$

然后我们可以发现e整除phi，所以他们二者是不互素的，不互素则逆元不存在，那为什么inverse函数还是能求解呢（虽然答案是错误的），其实我们可以打印一下使用inverse函数输出的d，会发现d=1，他并没有进行数据校验，而是会1。

那么此时我们该如何解决这个RSA问题，逆元不存在这说明对应的私钥不存在，难道是不可解了吗？

答案是否定的，我们可以考虑flag比较短，则flag转为数字后的数m足够小，则有

$$m\mathrm{mod}pq\equiv m\mathrm{mod}n$$

什么意思呢？也就是说m不仅比n（这里的n=pqr）还小也比pq还小，所以取模得到的结果也相同，那么此时有，设

$$c^1=c\mathrm{mod}pq=(m{}^e\mathrm{mod}n)\mathrm{mod}pq=m{}^e\mathrm{mod}pq$$

$$e{d}^1\equiv 1(\mathrm{mod}\phi (pq))$$

c₁^d₁​​ ≡ m(mod pq)

即c₁为c再模pq的结果，根据模的性质有c₁​便是消息使用公钥(pq,e)加密的结果，那么此时我们可以求出该公钥对应的私钥进行解密，得到m  mod  pq的结果，又因为m比较小，所以该结果直接就是m。

在实际计算中，我们其实并不需要额外写一句c1 = c % (p*q)，因为根据模的性质，只要最后进行了模运算即可。

其实通俗一点的理解就是当m比较小时，此时就算公钥对应的私钥不存在（逆元不存在），我们可以考虑将公钥转化为其他公钥（用原公钥因子进行重组）再尝试求解私钥进行解密，依然可以得到正确结果。

这里其实也就解释了为什么P7，P8需要加上大量字符串的填充，就是为了防止使用该方法直接解出，在现实世界的RSA算法应用标准中，明文其实都会用特定算法进行填充来防止这种情况出现。

exp:

from Crypto.Util.number import *
from gmpy2 import *

p = 7478755670255767435237487693415479182290330775502792675052667363676831056436638619069277770540533350723045234676443621124912287506103439704868369839725279
q = 9232828888049557325429111621080998490274442347556398052322580869768941301413255711626092627273543579067597113958627672298942570149816938335701615759283713
r = 102909133680612532601801231903654039
e = 65537
c = 142893174944324070830219394465469685943669308818639857030565389839224452373848570577201378981080333784852764502832587008270072323948511579823852437852643609820245476634896477031076952735298279618952398460203032125853063235638358942643559551563899381032067185778629120272032518475352761100115057449043142848203976076694124978394099839339406197

n = p*q*r
phi = (p-1)*(q-1)
d = invert(e, phi)
m = pow(c, d, p*q)

print(long_to_bytes(m))
#NSSCTF{no_inverse!but_decrypt}

[RSA1]P10(e与phi不互素）

题目

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(512)
q = getPrime(512)

e = 65537*2

n = p*q

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 9927950299160071928293508814174740578824022211226572614475267385787727188317224760986347883270504573953862618573051241506246884352854313099453586586022059
q = 9606476151905841036013578452822151891782938033700390347379468858357928877640534612459734825681004415976431665670102068256547092636766287603818164456689343
e = 131074
c = 68145285629092005589126591120307889109483909395989426479108244531402455690717006058397784318664114589567149811644664654952286387794458474073250495807456996723468838094551501146672038892183058042546944692051403972876692350946611736455784779361761930869993818138259781995078436790236277196516800834433299672560
'''

我的解答：

已知(e，p，q，c），但是e和phi不互素

我们需要先求出e和phi的最大公约数gcd₁ = 2 然后e/gcd₁ 和phi互素，其实是有

c = m^2e mod n = (m²)^e mod n

这里的gcd₁即是2，因此按正常步骤解出来的m其实是m² 即m^gcd₁ 最后需要我们开个根即可。

exp:

import gmpy2
import libnum

p = 9927950299160071928293508814174740578824022211226572614475267385787727188317224760986347883270504573953862618573051241506246884352854313099453586586022059
q = 9606476151905841036013578452822151891782938033700390347379468858357928877640534612459734825681004415976431665670102068256547092636766287603818164456689343
e = 131074
c = 68145285629092005589126591120307889109483909395989426479108244531402455690717006058397784318664114589567149811644664654952286387794458474073250495807456996723468838094551501146672038892183058042546944692051403972876692350946611736455784779361761930869993818138259781995078436790236277196516800834433299672560

n = p*q
phi = (p-1)*(q-1)
gcd1 = gmpy2.gcd(e, phi)
t1 = e//gcd1
dt = gmpy2.invert(t1, phi)
m_gcd1 = gmpy2.powmod(c, dt, n)
m = gmpy2.iroot(m_gcd1, gcd1)    # 得到元组 (mpz(1920535408007397829480400151650246901210634018403879187581), True)
flag = libnum.n2s(int(m[0]))
print(flag)
#NSSCTF{inverse_and_root}