ACTF 2023 部分WP
来自密码手的哀嚎:
玩不了一点,太难了。
CRYPTO
MDH
Description
Malin’s Diffile-Hellman Key Exchange.
task.sage
from hashlib import sha256
from secret import flag
r = 128
c = 96
p = 308955606868885551120230861462612873078105583047156930179459717798715109629
Fp = GF(p)
def gen():
a1 = random_matrix(Fp, r, c)
a2 = random_matrix(Fp, r, c)
A = a1 * a2.T
return (a1, a2), A
sk_alice, pk_alice = gen()
sk_bob, pk_bob = gen()
shared = (sk_alice[0].T * pk_bob * sk_alice[1]).trace()
ct = int(sha256(str(int(shared)).encode()).hexdigest(), 16) ^^ int.from_bytes(flag, 'big')
with open('output.txt', 'wb') as f:
f.write(str(ct).encode() + b'\n')
f.write(str(list(pk_alice)).encode() + b'\n')
f.write(str(list(pk_bob)).encode() + b'\n')output.txt
8308943029741424587523612386337754255889681699670071706719724435165094611096603769021839263
[(248911473252706126701034292146541373251616513930062195044617795903221826522, 2006663512374471656012713476848952481708164609054161957903243961884729327, 34477445744870695124522330116853976140397756578144976256418933561356297270, 134510431748375978099734325290614896206741166021565864231628975299374894934, 263052897010932566643732419798564392599203662525075356313352360336696893126, 141993015830421728697942660480086149608207938704594224742919997457007731362, 2884941569385999952542152446419918040970038754772386008722345958209977361, 251929132317823958330447233877195880589103297101688031807949769646459583779, 202402171486986340762120037260332866100215659317408872569460852300216859639, 299869910419680584431600458234987314403629236129755735947187138970557973965, 32123365781587714822724172153965985134547746672138349976513502380627017939,........分析一下:
shared = (sk_alice[0].T * pk_bob * sk_alice[1]).trace()
也就是说shared = ((a1)T * b1 * (b2)T * a2 ).trace()
已知Pk_alice = a1 * (a2)T 和Pk_bob = b1 * (b2)T
线性代数学的好的我们可以根据矩阵的迹的性质:Tr(A) = Tr(AT) ,Tr(AB) = Tr(BA)
因此我们可以把shared 内容交换下顺序得到 shared = ((a1)T * a2 * (b2)T * b1 ).trace()
即shared = (Pk_alice.T * Pk_bob).trace()
exp:
from hashlib import sha256
p = 308955606868885551120230861462612873078105583047156930179459717798715109629
Fq = GF(p)
f = open("output.txt",'r')
data = f.readlines()
ct = eval(data[0])
pk_alice = eval(data[1])
pk_bob = eval(data[2])
pk_alice = Matrix(Fp,pk_alice)
pk_bob = Matrix(Fq,pk_bob)
shared = (pk_alice.T * pk_bob).trace()
m = int(sha256(str(int(shared)).encode()).hexdigest(), 16) ^^ ct
flag = bytes.fromhex(hex(m)[2:])
print(flag)
# ACTF{do_you_know_f0rm2l1n_1s_4w3s0m3!}EasyRSA
Description
EasyRSA
from secret import flag
from Crypto.Util.number import *
def genKey(nbits, dbits):
bbits = (nbits // 2 - dbits) // 2
while True:
a = getRandomNBitInteger(dbits)
b = getRandomNBitInteger(bbits)
c = getRandomNBitInteger(bbits)
p1 = a * b * c + 1
if isPrime(p1):
# print("p1 =", p1)
break
while True:
d = getRandomNBitInteger(dbits)
p2 = b * c * d + 1
if isPrime(p2):
# print("p2 =", p2)
break
while True:
e = getRandomNBitInteger(bbits)
f = getRandomNBitInteger(bbits)
q1 = e * d * f + 1
p3 = a * e * f + 1
if isPrime(q1) and isPrime(p3):
# print("p3 =", p3)
# print("q1 =", q1)
break
while True:
d_ = getRandomNBitInteger(dbits)
if GCD(a * b * c * d * e * f, d_) != 1:
continue
e_ = inverse(d_, a * b * c * d * e * f)
k1 = (e_ * d_ - 1) // (a * b * c * d * e * f)
assert e_ * d_ == (a * b * c * d * e * f) * k1 + 1
q2 = k1 * e * f + 1
q3 = k1 * b * c + 1
if isPrime(q2) and isPrime(q3):
# print("q2 =", q2)
# print("q3 =", q3)
# print("e =", e_)
# print("d =", d_)
break
n1 = p1 * q1
n2 = p2 * q2
n3 = p3 * q3
assert pow(pow(0xdeadbeef, e_, n1), d_, n1) == 0xdeadbeef
assert pow(pow(0xdeadbeef, e_, n2), d_, n2) == 0xdeadbeef
assert pow(pow(0xdeadbeef, e_, n3), d_, n3) == 0xdeadbeef
return(e_, n1, n2, n3)
nbits = 0x600
dbits = 0x210
m = bytes_to_long(flag)
e, n1, n2, n3 = genKey(nbits, dbits)
c = pow(m, e, n1)
print("c =", c)
print("e =", e)
print("n1 =", n1)
print("n2 =", n2)
print("n3 =", n3)
# c = 63442255298812942222810837512019302954917822996915527697525497640413662503768308023517128481053593562877494934841788054865410798751447333551319775025362132176942795107214528962480350398519459474033659025815248579631003928932688495682277210240277909527931445899728273182691941548330126199931886748296031014210795428593631253184315074234352536885430181103986084755140024577780815130067722355861473639612699372152970688687877075365330095265612016350599320999156644
# e = 272785315258275494478303901715994595013215169713087273945370833673873860340153367010424559026764907254821416435761617347240970711252213646287464416524071944646705551816941437389777294159359383356817408302841561284559712640940354294840597133394851851877857751302209309529938795265777557840238332937938235024502686737802184255165075195042860413556866222562167425361146312096189555572705076252573222261842045286782816083933952875990572937346408235562417656218440227
# n1 = 473173031410877037287927970398347001343136400938581274026578368211539730987889738033351265663756061524526288423355193643110804217683860550767181983527932872361546531994961481442866335447011683462904976896894011884907968495626837219900141842587071512040734664898328709989285205714628355052565784162841441867556282849760230635164284802614010844226671736675222842060257156860013384955769045790763119616939897544697150710631300004180868397245728064351907334273953201
# n2 = 327163771871802208683424470007561712270872666244394076667663345333853591836596054597471607916850284565474732679392694515656845653581599800514388800663813830528483334021178531162556250468743461443904645773493383915711571062775922446922917130005772040139744330987272549252540089872170217864935146429898458644025927741607569303966038195226388964722300472005107075179204987774627759625183739199425329481632596633992804636690274844290983438078815836605603147141262181
# n3 = 442893163857502334109676162774199722362644200933618691728267162172376730137502879609506615568680508257973678725536472848428042122350184530077765734033425406055810373669798840851851090476687785235612051747082232947418290952863499263547598032467577778461061567081620676910480684540883879257518083587862219344609851852177109722186714811329766477552794034774928983660538381764930765795290189612024799300768559485810526074992569676241537503405494203262336327709010421参考:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4276937
分析如下:
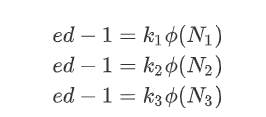
于是有:
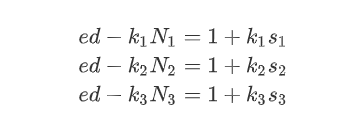
构造格:
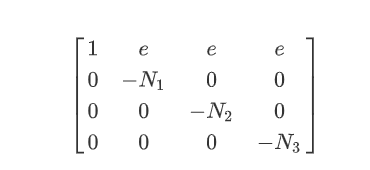
调至平衡后,LLL即可得d,exp:
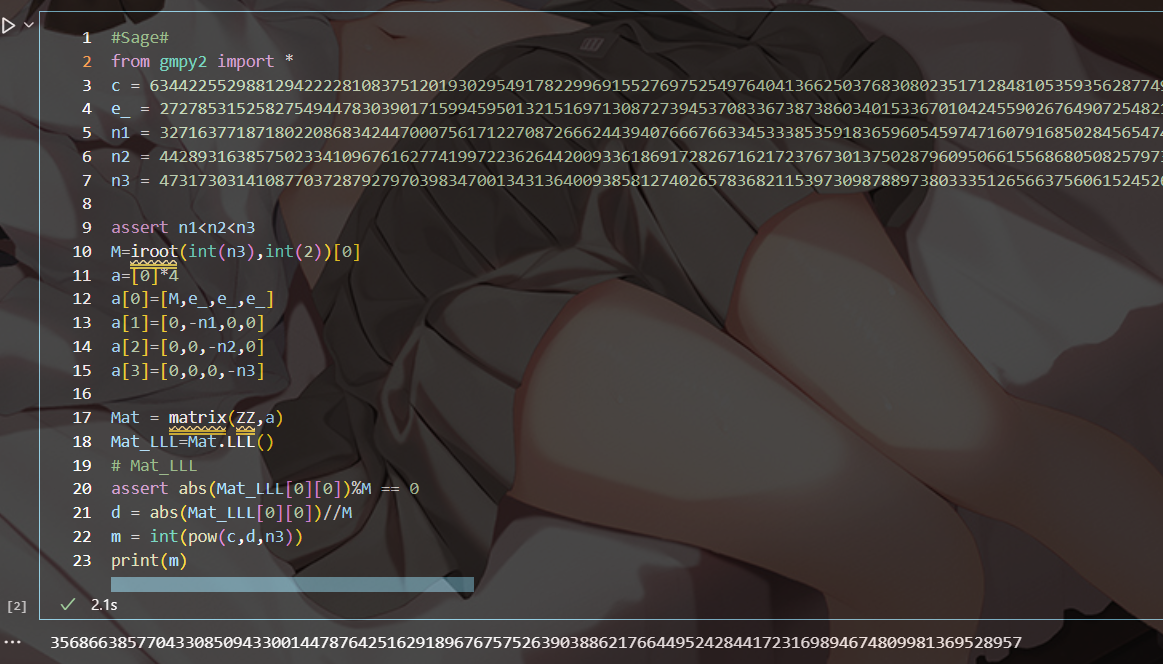
#Sage#
from gmpy2 import *
c = 63442255298812942222810837512019302954917822996915527697525497640413662503768308023517128481053593562877494934841788054865410798751447333551319775025362132176942795107214528962480350398519459474033659025815248579631003928932688495682277210240277909527931445899728273182691941548330126199931886748296031014210795428593631253184315074234352536885430181103986084755140024577780815130067722355861473639612699372152970688687877075365330095265612016350599320999156644
e_ = 272785315258275494478303901715994595013215169713087273945370833673873860340153367010424559026764907254821416435761617347240970711252213646287464416524071944646705551816941437389777294159359383356817408302841561284559712640940354294840597133394851851877857751302209309529938795265777557840238332937938235024502686737802184255165075195042860413556866222562167425361146312096189555572705076252573222261842045286782816083933952875990572937346408235562417656218440227
n1 = 327163771871802208683424470007561712270872666244394076667663345333853591836596054597471607916850284565474732679392694515656845653581599800514388800663813830528483334021178531162556250468743461443904645773493383915711571062775922446922917130005772040139744330987272549252540089872170217864935146429898458644025927741607569303966038195226388964722300472005107075179204987774627759625183739199425329481632596633992804636690274844290983438078815836605603147141262181
n2 = 442893163857502334109676162774199722362644200933618691728267162172376730137502879609506615568680508257973678725536472848428042122350184530077765734033425406055810373669798840851851090476687785235612051747082232947418290952863499263547598032467577778461061567081620676910480684540883879257518083587862219344609851852177109722186714811329766477552794034774928983660538381764930765795290189612024799300768559485810526074992569676241537503405494203262336327709010421
n3 = 473173031410877037287927970398347001343136400938581274026578368211539730987889738033351265663756061524526288423355193643110804217683860550767181983527932872361546531994961481442866335447011683462904976896894011884907968495626837219900141842587071512040734664898328709989285205714628355052565784162841441867556282849760230635164284802614010844226671736675222842060257156860013384955769045790763119616939897544697150710631300004180868397245728064351907334273953201
assert n1<n2<n3
M=iroot(int(n3),int(2))[0]
a=[0]*4
a[0]=[M,e_,e_,e_]
a[1]=[0,-n1,0,0]
a[2]=[0,0,-n2,0]
a[3]=[0,0,0,-n3]
Mat = matrix(ZZ,a)
Mat_LLL=Mat.LLL()
# Mat_LLL
assert abs(Mat_LLL[0][0])%M == 0
d = abs(Mat_LLL[0][0])//M
m = int(pow(c,d,n3))
print(m)
#35686638577043308509433001447876425162918967675752639038862176644952428441723169894674809981369528957from Crypto.Util.number import long_to_bytes
m = 35686638577043308509433001447876425162918967675752639038862176644952428441723169894674809981369528957
print('💌:',long_to_bytes(m))
#💌: b'ACTF{5FFC427B-F14F-DCA0-C425-675B149890C2}'MidRSA
Description
MidRSA
from secret import flag
from Crypto.Util.number import *
def genKey(nbits, dbits):
bbits = (nbits // 2 - dbits) // 2
while True:
a = getRandomNBitInteger(dbits)
b = getRandomNBitInteger(bbits)
c = getRandomNBitInteger(bbits)
p1 = a * b * c + 1
if isPrime(p1):
# print("p1 =", p1)
break
while True:
d = getRandomNBitInteger(dbits)
p2 = b * c * d + 1
if isPrime(p2):
# print("p2 =", p2)
break
while True:
e = getRandomNBitInteger(bbits)
f = getRandomNBitInteger(bbits)
q1 = e * d * f + 1
p3 = a * e * f + 1
if isPrime(q1) and isPrime(p3):
# print("p3 =", p3)
# print("q1 =", q1)
break
while True:
d_ = getRandomNBitInteger(dbits)
if GCD(a * b * c * d * e * f, d_) != 1:
continue
e_ = inverse(d_, a * b * c * d * e * f)
k1 = (e_ * d_ - 1) // (a * b * c * d * e * f)
assert e_ * d_ == (a * b * c * d * e * f) * k1 + 1
q2 = k1 * e * f + 1
q3 = k1 * b * c + 1
if isPrime(q2) and isPrime(q3):
# print("q2 =", q2)
# print("q3 =", q3)
# print("e =", e_)
print("d =", d_)
break
n1 = p1 * q1
n2 = p2 * q2
n3 = p3 * q3
assert pow(pow(0xdeadbeef, e_, n1), d_, n1) == 0xdeadbeef
assert pow(pow(0xdeadbeef, e_, n2), d_, n2) == 0xdeadbeef
assert pow(pow(0xdeadbeef, e_, n3), d_, n3) == 0xdeadbeef
return(e_, n1, n2, n3)
nbits = 0x600
dbits = 0x240
m = bytes_to_long(flag)
e, n1, n2, n3 = genKey(nbits, dbits)
c = pow(m, e, n1)
print("c =", c)
print("e =", e)
print("n1 =", n1)
print("n2 =", n2)
print("n3 =", n3)
# c = 598823083137858565473505718525815255620672892612784824187302545127574115000325539999824374357957135208478070797113625659118825530731575573239221853507638809719397849963861367352055486212696958923800593172417262351719477530809870735637329898331854130533160020420263724619225174940214193740379571953951059401685115164634005411478583529751890781498407518739069969017597521632392997743956791839564573371955246955738575593780508817401390102856295102225132502636316844
# e = 334726528702628887205076146544909357751287869200972341824248480332256143541098971600873722567713812425364296038771650383962046800505086167635487091757206238206029361844181642521606953049529231154613145553220809927001722518303114599682529196697410089598230645579658906203453435640824934159645602447676974027474924465177723434855318446073578465621382859962701578350462059764095163424218813852195709023435581237538699769359084386399099644884006684995755938605201771
# n1 = 621786427956510577894657745225233425730501124908354697121702414978035232119311662357181409283130180887720760732555757426221953950475736078765267856308595870951635246720750862259255389006679454647170476427262240270915881126875224574474706572728931213060252787326765271752969318854360970801540289807965575654629288558728966771231501959974533484678236051025940684114262451777094234017210230731492336480895879764397821363102224085859281971513276968559080593778873231
# n2 = 335133378611627373902246132362791381335635839627660359611198202073307340179794138179041524058800936207811546752188713855950891460382258433727589232119735602364790267515558352318957355100518427499530387075144776790492766973547088838586041648900788325902589777445641895775357091753360428198189998860317775077739054298868885308909495601041757108114540069950359802851809227248145281594107487276003206931533768902437356652676341735882783415106786497390475670647453821
# n3 = 220290953009399899705676642623181513318918775662713704923101352853965768389363281894663344270979715555659079125651553079702318700200824118622766698792556506368153467944348604006011828780474050012010677204862020009069971864222175380878120025727369117819196954091417740367068284457817961773989542151049465711430065838517386380261817772422927774945414543880659243592749932727798690742051285364898081188510009069286094647222933710799481899960520270189522155672272451改写等式,爆破d_低16位,构建格求解。
对于
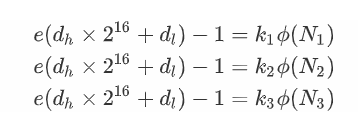
有
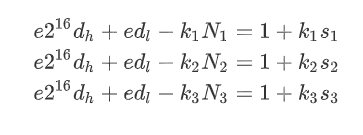
构造格:
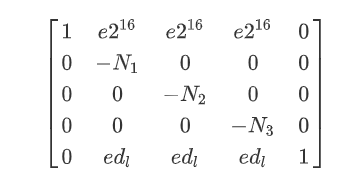
调至平衡后,LLL求得d的高位
然后拼接d的低位后,即恢复d,exp:
#Sage#
from gmpy2 import *
from tqdm import tqdm
from Crypto.Util.number import *
c = 598823083137858565473505718525815255620672892612784824187302545127574115000325539999824374357957135208478070797113625659118825530731575573239221853507638809719397849963861367352055486212696958923800593172417262351719477530809870735637329898331854130533160020420263724619225174940214193740379571953951059401685115164634005411478583529751890781498407518739069969017597521632392997743956791839564573371955246955738575593780508817401390102856295102225132502636316844
e_ = 334726528702628887205076146544909357751287869200972341824248480332256143541098971600873722567713812425364296038771650383962046800505086167635487091757206238206029361844181642521606953049529231154613145553220809927001722518303114599682529196697410089598230645579658906203453435640824934159645602447676974027474924465177723434855318446073578465621382859962701578350462059764095163424218813852195709023435581237538699769359084386399099644884006684995755938605201771
n3 = 621786427956510577894657745225233425730501124908354697121702414978035232119311662357181409283130180887720760732555757426221953950475736078765267856308595870951635246720750862259255389006679454647170476427262240270915881126875224574474706572728931213060252787326765271752969318854360970801540289807965575654629288558728966771231501959974533484678236051025940684114262451777094234017210230731492336480895879764397821363102224085859281971513276968559080593778873231
n2 = 335133378611627373902246132362791381335635839627660359611198202073307340179794138179041524058800936207811546752188713855950891460382258433727589232119735602364790267515558352318957355100518427499530387075144776790492766973547088838586041648900788325902589777445641895775357091753360428198189998860317775077739054298868885308909495601041757108114540069950359802851809227248145281594107487276003206931533768902437356652676341735882783415106786497390475670647453821
n1 = 220290953009399899705676642623181513318918775662713704923101352853965768389363281894663344270979715555659079125651553079702318700200824118622766698792556506368153467944348604006011828780474050012010677204862020009069971864222175380878120025727369117819196954091417740367068284457817961773989542151049465711430065838517386380261817772422927774945414543880659243592749932727798690742051285364898081188510009069286094647222933710799481899960520270189522155672272451
n1,n2,n3 = sorted([n1,n2,n3])
assert n1<n2<n3
def solve():
for dl in tqdm(range(2^16)):
a=[0]*5
a[0]=[2^(16+767),e_*2^16,e_*2^16,e_*2^16,0]
a[1]=[0,-n1,0,0,0]
a[2]=[0,0,-n2,0,0]
a[3]=[0,0,0,-n3,0]
a[4]=[0,e_*dl,e_*dl,e_*dl,2^(576+767)]
Mat = matrix(ZZ,a)
Mat_LLL=Mat.LLL()
for line in Mat_LLL:
if (abs(line[-1]) == 2^(576+767)):
dh = abs(line[0])//2^(16+767)
d = int((dh<<16)+dl)
m = int(pow(c,d,n1))
flag1 = long_to_bytes(m)
m = int(pow(c,d,n2))
flag2 = long_to_bytes(m)
m = int(pow(c,d,n3))
flag3 = long_to_bytes(m)
flags = [flag1, flag2,flag3]
for f in flags:
if b'ACTF{' in f:
print(f)
return
solve() # ACTF{D16C46D9-77A2-2D96-CA51-4538EFB6AFF7}claw crane
Description
抓娃娃咯 / Grabbing Dolls
Service
Access via
nc 152.136.172.227 22222
查看代码
#!/usr/bin/env python3
from Crypto.Util.number import (
bytes_to_long, long_to_bytes
)
from hashlib import md5
import os, signal
import sys
import random
BITS = 128
class ClawCrane(object):
def __init__(self) -> None:
self.seed = bytes_to_long(os.urandom(BITS//8))
self.bless = 0
self.score = 0
def get_input(self, prompt="> "):
print(prompt, end="")
sys.stdout.flush()
return input()
def check_pos(self, pos, moves):
col, row = 0, 0
for move in moves:
if move == "W":
if row < 15: row += 1
elif move == "S":
if row > 0: row -= 1
elif move == "A":
if col > 0: col -= 1
elif move == "D":
if col < 15: col += 1
else:
return -1
print(col, row)
return pos == [col, row]
def gen_chaos(self, inp):
def mapping(x):
if x=='W': return "0"
if x=='S': return "1"
if x=='A': return "2"
if x=='D': return "3"
vs = int("".join(map(mapping, inp)), 4)
chaos = bytes_to_long(md5(
long_to_bytes((self.seed + vs) % pow(2,BITS))
).digest())
self.seed = (self.seed + chaos + 1) % pow(2,BITS)
return chaos
def destiny_claw(self, delta):
bits = bin(delta)[2:]
if len(bits) < 128+self.bless:
bits += "0"*(128+self.bless - len(bits))
c = random.choice(bits)
if c=='0': return True
else: return False
def run(self):
pos = [random.randrange(1,16), random.randrange(1,16)]
moves = self.get_input(f"i am at {pos}, claw me.\nYour moves: ")
if len(moves) > 100:
print("too many steps")
return
if not self.check_pos(pos, moves):
print("sorry, clawed nothing")
return
r = self.gen_chaos(moves[:64])
print(f"choas: {r}")
p, q = map(int, self.get_input(f"give me your claw using p,q and p,q in [0, 18446744073709551615] (e.g.: 1,1): ").split(","))
if not (p>0 and p<pow(2,BITS//2) and q>0 and q<pow(2,BITS//2)):
print("not in range")
return
delta = abs(r*q - p*pow(2,BITS))
if self.destiny_claw(delta):
self.score += 10
self.bless = 0
print("you clawed it")
else:
self.bless += 16
print("sorry, clawed nothing")
import hashlib
import os
def generate_proof_of_work(size,difficulty):
target = os.urandom(size).hex()
hash_value = hashlib.sha1(target.encode()).hexdigest()
return target[difficulty:],hash_value
def check_proof_of_work(prefix,suffix,expected):
return hashlib.sha1(f'{prefix}{suffix}'.encode()).hexdigest()==expected
def proof():
POW_SIZE=32
POW_DIFFICULTY=6
suff,hs=generate_proof_of_work(POW_SIZE,POW_DIFFICULTY)
print(f'sha1(prefix+"{suff}")=={hs}')
pref=input("prefix = ?\n")
if not check_proof_of_work(pref,suff,hs):
print("PoW error")
exit(1)
def main():
signal.alarm(600)
proof()
cc = ClawCrane()
for _ in range(256):
try:
cc.run()
print(f"your score: {cc.score}")
except:
print(f"abort")
break
if cc.score >= 2220:
print(f"flag: {open('/flag.txt').read()}")
if __name__ == "__main__":
main()题目的终极目标是拿到2220分,即256次交互至少有222次得分,是个相当大的概率。
第一想法有两个:
一个是在34次交互内拿到某个必要条件(比如seed值)以达成题目通过。
另一个是利用某种办法控制通关概率在相当高的水平,跑几次脚本通关。
那么在开始得分前,我们简单分析流程,首先得把它的得分步骤给搞清楚。
题目给出一个坐标,并且要求我们在100次移动内从0,0位置移动到目标坐标,移动字符串使用AWSD进行表示,如果移动指令没能成功完成移动操作,那么这次交互机会就会被浪费。
def check_pos(self, pos, moves):
col, row = 0, 0
for move in moves:
if move == "W":
if row < 15: row += 1
elif move == "S":
if row > 0: row -= 1
elif move == "A":
if col > 0: col -= 1
elif move == "D":
if col < 15: col += 1
else:
return -1
print(col, row)
return pos == [col, row]这个字符串在编码成数字以后,直接影响到随机种子的前进。
def gen_chaos(self, inp):
def mapping(x):
if x=='W': return "0"
if x=='S': return "1"
if x=='A': return "2"
if x=='D': return "3"
vs = int("".join(map(mapping, inp)), 4)
chaos = bytes_to_long(md5(
long_to_bytes((self.seed + vs) % pow(2,BITS))
).digest())
self.seed = (self.seed + chaos + 1) % pow(2,BITS)
return chaosr = self.gen_chaos(moves[:64])
看到这里的想法是chaos是能够被操控利用的,我们可以在move的前64bit填上任意的移动方式来控制vs的值,比如我们控制第一个vs为0,前一次的chaos操作让它满足seed1 = seed0+chaos+1,chaos已知,那么这时候我们令vs1+chaos+1 = 2^128,就能够令chaos1 = md5(seed)=chaos,有seed2 = seed1+chaos+1+chaos1+1,再令vs2+(chaos+1+chaos1+1) = 2^128.....这样我们就能够永远控制输出的chaos为一个相同的值。
而chaos相同的用处很显然就来自于可以影响最后抽奖的结果。现在只要我们能够找到一组数据,使delta中0的部分占比很大,就能够完成这个问题的求解。
r = self.gen_chaos(moves[:64])
print(f"choas: {r}")
p, q = map(int, self.get_input(f"give me your claw using p,q and p,q in [0, 18446744073709551615] (e.g.: 1,1): ").split(","))
if not (p>0 and p<pow(2,BITS//2) and q>0 and q<pow(2,BITS//2)):
print("not in range")
return
delta = abs(r*q - p*pow(2,BITS))
if self.destiny_claw(delta):
self.score += 10
self.bless = 0
print("you clawed it")
else:
self.bless += 16
print("sorry, clawed nothing")
p和q是我们自己构造的(0,2^64)之间的数字,我们生成一个rq-p2^128形式的数字(也可以理解为在操作rq%2^128),如果在二进制中抽奖抽到0,则进行加分。如果我们要在256次判定中得到222次成功,最好需要保证128个二进制位中有111个0,这里可能需要捏个格去进行求解。所以我们使用了一个基础的格子,求解得到64bit的短向量delta,p,在p为小参数的同时,q一定也为小参数。
from hashlib import sha256,md5
from pwn import *
context.log_level = 'debug'
import re
import gmpy2
import libnum
p = remote('152.136.172.227',22222)
def num2awds(num):
mov_abt = 'WSAD'
aim = ''
for i in range(128):
aim = mov_abt[num%4] + aim
num //= 4
return aim
def mov_construct(end,head):
xend,yend = end
x,y = 0,0
for i in head:
if i == 'W':
if y < 15: y += 1
elif i == 'S':
if y > 0: y -= 1
elif i == 'A':
if x > 0: x -= 1
elif i == 'D':
if x < 15: x += 1
if x > xend:
for i in range(x-xend):
head += 'A'
else:
for i in range(xend-x):
head += 'D'
if y > yend:
for i in range(y-yend):
head += 'S'
else:
for i in range(yend-y):
head += 'W'
return head
for i in range(256):
a = p.recvline().decode()
a = a.split(' ')
x,y = int(a[3][1:-1]),int(a[4][:-2])
p.recvuntil(b'Your moves: ')
p.sendline(mov_construct((x,y),'W'*64).encode())
p.recvline()
chaos = int(p.recvline()[7:].decode())
p.recvuntil(b'(e.g.: 1,1): ')
p.sendline(b'1,2')
p.recvuntil(b'your score:')
p.recvline()普通跑一轮是1410,接下来固定r试试,固定r+格64,可以打到2020,还差200分。目前这个脚本大概是稳1800,我感觉直接LLL不是求出最少1的最好的方法,可能还得往上做改进。
from hashlib import sha256,md5
from pwn import *
context.log_level = 'debug'
import re
import gmpy2
import libnum
p = remote('152.136.172.227',22222)
def num2awds(num):
mov_abt = 'WSAD'
aim = ''
for i in range(64):
aim = mov_abt[num%4] + aim
num //= 4
return aim
def mov_construct(end,head):
xend,yend = end
x,y = 0,0
for i in head:
if i == 'W':
if y < 15: y += 1
elif i == 'S':
if y > 0: y -= 1
elif i == 'A':
if x > 0: x -= 1
elif i == 'D':
if x < 15: x += 1
if x > xend:
for i in range(x-xend):
head += 'A'
else:
for i in range(xend-x):
head += 'D'
if y > yend:
for i in range(y-yend):
head += 'S'
else:
for i in range(yend-y):
head += 'W'
return head
a = p.recvline().decode()
a = a.split(' ')
x,y = int(a[3][1:-1]),int(a[4][:-2])
p.recvuntil(b'Your moves: ')
p.sendline(mov_construct((x,y),'W'*64).encode())
p.recvline()
chaos = int(p.recvline()[7:].decode())
tmp = chaos+1
print(tmp)
p.recvuntil(b'(e.g.: 1,1): ')
p.sendline(b'1,2')
p.recvuntil(b'your score:')
p.recvline()
P,Q = int(input()),int(input())
for i in range(256):
a = p.recvline().decode()
a = a.split(' ')
x,y = int(a[3][1:-1]),int(a[4][:-2])
p.recvuntil(b'Your moves: ')
cnum = int((-tmp)%2**128)
print('cnum:',cnum)
p.sendline(mov_construct((x,y),num2awds(cnum)).encode())
p.recvline()
chaos = int(p.recvline()[7:].decode())
tmp += chaos+1
p.recvuntil(b'(e.g.: 1,1): ')
p.sendline(f'{P},{Q}'.encode())
p.recvuntil(b'your score:')
p.recvline()
a = 239996570097549520897992758078844507254
b = 2^128
m = matrix([[a,1],[b,0]])
print(m.LLL())
p = 8750581204523477797
q = (a*p-22959585545265104654)/b
print(q)
print(a*p-b*q) 
找到新窍门!令结果为负值,q加一个2^63就会形成这种效果(得保证在界内):
-0b100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010100101100101100010011110001100011010000100110011110010110110if len(bits) < 128+self.bless:
bits += "0"*(128+self.bless - len(bits))把长度拉伸至192,这样题目zfill的128就变成了192,从而通过改变字长来达到提高正确率的效果,相当于自带了4次bless。跑几遍脚本就可以拿到一组通过2220的数据。
a = 182169930054624761546696716074077090774
b = 2^128
m = matrix([[a,1],[b,0]])
print(m.LLL())
p = 6207226441042315485
print(p > 2^64)
q = (a*p+10341573661598863426)/b
print(q+2^63)
print((q+2^63 ) > 2^64)MISC
SIGNIN: 东方原神大学(签到题)
Description
1944 年,英国剑桥大学著名生物化学家李约瑟来到浙江大学,并盛赞浙江大学是“东方剑桥”,浙大也通过矢志不渝的发展和进步,证明了自己的含金量。
2020 年,开放冒险游戏原神横空出世,世界各地的游戏玩家都被这个具有宏大世界观并蕴含丰富中华传统文化的佳作所吸引,就连 AAA 战队的指导老师 BlackWhite 都赞其颇有塞尔达之神韵。
在接下来的几年间,各大高校间兴起了一阵原神大学之风,中国石油大学轻添寥寥数笔,便将自己的校名改为了中国原神大学,而哈尔滨工业大学也接下了建设提瓦特工业大学的光荣使命,众多学校也进入了原神大学称号的抢夺战之中。然而,作为全国排名第三的大学,浙江大学还没有自己的原神大学称号。这时浙江大学 AAA 的队员们想起了李约瑟对浙大“东方剑桥”的盛赞,恍然大悟,浙江大学不就是东方原神大学吗!
所以,欢迎来到东方提瓦特大陆
刚开始做这个就知道点进官网翻翻,一脸懵逼不知道干啥,源代码啥也没有,看着他们一个个做出来。。。呜呜难受
后来才知道用curl发送一个请求从而获取该网站的内容,哎
curl http://www.东方原神大学.com/得到:

SIGNOUT(签退题)
填问卷得flag。。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署
· 葡萄城 AI 搜索升级:DeepSeek 加持,客户体验更智能