crypto常用算法
欧几里得算法(辗转相除法)

def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)扩展欧几里得算法

def ext_euclid(a, b):
if b == 0:
return 1, 0, a
else:
x, y, q = ext_euclid(b, a % b)
x, y = y, (x - (a // b) * y)
return x, y, q大步小步算法(BSGS算法)

//C++
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
typedef long long LL;
LL quick_mod(LL a, LL b, LL c)//费马小定理+快速幂求逆元
{
LL ans = 1;
while (b)
{
if (b % 2 == 1)
ans = (ans*a) % c;
b /= 2;
a = (a*a) % c;
}
return ans;
}
int log_mod(int a, int b, int n)
{
int m, v, e = 1, i;
m = (int)sqrt(n + 0.5);
v = quick_mod(quick_mod(a, m, n),n-2, n);
map<int, int> x;
x[1] = 0;
for (int i = 1; i < m; i++) {
e = e*a%n;
if (!x.count(e)) x[e] = i;
}
for (i = 0; i < m; i++) {
if (x.count(b)) return i*m + x[b];
b = b*v%n;
}
return -1;
}#python
def BSGS(g, y, p):
m = int(sqrt(p))
if not is_square(p):
m += 1
S = {pow(g, j, p): j for j in range(m)}
gs = pow(g, inverse(m, p), p)
for i in range(m):
if y in S:
return i * m + S[y]
y = y * gs % p
return None扩展大步小步算法(扩展BSGS算法)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int gcd(int a,int b){
if(!b)
return a;
else{
while(int i=a%b){
a=b;
b=i;
}
return b;
}
}
inline int qpow(ll a,int n,int m) {
//这个快速幂保证p不是1,少模一次是一次
ll s=1;
while(n) {
if(n&1)
s=s*a%m;
a=a*a%m;
n>>=1;
}
return s;
}
unordered_map<int,int> M;
//要求a,n互质 a^x=b mod n .k,t是留给exbsgs调用的
int bsgs(int a,int b,int n,int k=1,int t=0) {
if(b==1)
return 0;
M.clear();
int m=ceil(sqrt(n));
ll s=b;//BS
for(int i=0; i<m; i++,s=s*a%n)
M[s]=i;
s=k;//GS
k=qpow(a,m,n);
for(ll i=1; i<=m; i++) {
s=s*k%n;
if(M.count(s))
return i*m-M[s]+t; //这样就保证找到的是最小解了
}
return -1;
}
//a^x=b mod n
int exbsgs(int a,int b,int n) {
if(b==1) {
return 0;
}
int d=gcd(a,n),k=1,t=0;
while(d^1) {
if(b%d) {
return -1;
}
++t;
b/=d;
n/=d;
k=(ll)k*(a/d)%n;
if(b==k) {
return t;
}
d=gcd(a,n);
}
return bsgs(a,b,n,k,t);
}
int main() {
int a,b,n;
while(1) {
scanf("%d%d%d",&a,&n,&b);
if(!a&&!n&&!b)
break;
a%=n;
b%=n;
int ans=exbsgs(a,b,n);
if(ans==-1)
puts("No Solution");
else
printf("%d\n",ans);
}
return 0;
}威尔逊定理

欧拉定理

费马小定理

费马商

中国剩余定理(孙子定理 / CRT)


#sage
def chinese_remainder(modulus, remainders):
Sum = 0
prod = reduce(lambda a, b: a*b, modulus)
for m_i, r_i in zip(modulus, remainders):
p = prod // m_i
Sum += r_i * (inverse_mod(p,m_i)*p)
return Sum % prod
chinese_remainder([3,5,7],[2,3,2]) #23扩展中国剩余定理(扩展CRT / ExCRT)

#互质与不互质两种情况下都能工作良好的中国剩余定理(解同余方程组)
def GCRT(mi, ai):
# mi,ai分别表示模数和取模后的值,都为列表结构
assert (isinstance(mi, list) and isinstance(ai, list))
curm, cura = mi[0], ai[0]
for (m, a) in zip(mi[1:], ai[1:]):
d = gmpy2.gcd(curm, m)
c = a - cura
assert (c % d == 0) #不成立则不存在解
K = c / d * gmpy2.invert(curm / d, m / d)
cura += curm * K
curm = curm * m / d
return (cura % curm, curm) #(解,最小公倍数)变种1:Noisy CRT

参考:
Noisy Polynomial Interpolation and Noisy Chinese Remaindering
DeadSec CTF 2023 - Loud系列
费马因式分解

import gmpy2
from Crypto.Util.number import *
def factor(n):
a = gmpy2.iroot(n, 2)[0]
while 1:
B2 = pow(a, 2) - n
if gmpy2.is_square(B2):
b = gmpy2.iroot(B2, 2)[0]
p = a + b
q = a - b
return p, q
a += 1from gmpy2 import *
def fermat_factorization(n):
factor_list = []
get_context().precision = 2048
x = int(sqrt(n))
print(x)
while True:
x += 1
y2 = x ** 2 - n
if is_square(y2):
print('x = ',x)
y2 = mpz(y2)
get_context().precision = 2048
y = int(sqrt(y2))
factor_list.append([x+y, x-y])
if len(factor_list) == 2:
break
return factor_list高斯整数

z =
GI = GaussianIntegers()
GI(z).factor()
#因子组合CopperSmith攻击

#Sage
#单元
PR.<x> = PolynomialRing(Zmod(n))
f = (a + x)^e - c
root = f.small_roots(X=2^256, beta=1)[0] # find root < 2^256 with factor = n
#调参,增大格
#beta=0.48, epsilon=0.02
#多元
import itertools
def small_roots(f, bounds, m=1, d=None):
if not d:
d = f.degree()
R = f.base_ring()
N = R.cardinality()
f /= f.coefficients().pop(0)
f = f.change_ring(ZZ)
G = Sequence([], f.parent())
for i in range(m+1):
base = N^(m-i) * f^i
for shifts in itertools.product(range(d), repeat=f.nvariables()):
g = base * prod(map(power, f.variables(), shifts))
G.append(g)
B, monomials = G.coefficient_matrix()
monomials = vector(monomials)
factors = [monomial(*bounds) for monomial in monomials]
for i, factor in enumerate(factors):
B.rescale_col(i, factor)
B = B.dense_matrix().LLL()
B = B.change_ring(QQ)
for i, factor in enumerate(factors):
B.rescale_col(i, 1/factor)
H = Sequence([], f.parent().change_ring(QQ))
for h in filter(None, B*monomials):
H.append(h)
I = H.ideal()
if I.dimension() == -1:
H.pop()
elif I.dimension() == 0:
roots = []
for root in I.variety(ring=ZZ):
root = tuple(R(root[var]) for var in f.variables())
roots.append(root)
return roots
return []
PR.<a, b> = PolynomialRing(Zmod(n))
f = 4*r^2*a*b + 2*r*(a+b) + 1 - n
roots = small_roots(f, (2^256, 2^256), m=3)
a, b = roots[0]
PR.<x, y> = PolynomialRing(Zmod(q)) # n = x*y
# PR.<x, y> = Polygen(RealField(1000)) # n ≈ x*y
f = (2^256 * a + x) * s - (2^256 + 1) * y * b - c
roots = small_roots(f, [2^256, 2^256], m=4, d=4)
#其他多元
load('coppersmith.sage')
P.<x, y> = PolynomialRing(GF(p))
f = 2^170 * a^2 + 2^86 * a * x + x^2 - 2^85 * b + c - y
roots = coron(f, X=2^85, Y=2^85, k=1, debug=True)Gröbner基
空间和域

理想

Gröbner基定义

#Sage
###ZZ/QQ/RR
#Example-1
P.<x, y> = PolynomialRing(QQ)
f1 = x^2 + x*y - 10
f2 = x^3 + x^2*y - 20
f3 = x^4 + x*y^3 - 70
G = Ideal([f1, f2, f3]).groebner_basis()
print(G)
#Example-2
PR = PolynomialRing(Zmod(N), 'x', len(Cs))
x = PR.gens()
f1 = (65537*x[0] - 66666*x[1] + 12345*x[2] - x[3])
f2 = x[0] + x[1] + x[2] - s
Fs = [f1, f2]
Fs.extend([(x[i]**e - Cs[i]) for i in range(l)])
I = Ideal(Fs)
B = I.groebner_basis()
print(B)
m = ''
for b in B:
assert b.degree() == 1
mi = ZZ(-b(0, 0, 0, 0))
print(mi)
###Zmod(p)
from sage.matrix.matrix2 import Matrix
def resultant(f1, f2, var):
return Matrix.determinant(f1.sylvester_matrix(f2, var))
P.<Rx, Ry, Qx, Qy> = PolynomialRing(Zmod(p))
f1 = Ry^2 - Rx^3 - a*Rx - b
f2 = Qy^2 - Qx^3 - a*Qx - b
f3 = (Qy + Ry)^2 + (Qx - Rx)^2 * (- Rx - Qx - Px)
f4 = (- Qy - Ry) * (Rx - Px) + (Qx - Rx) * (- Ry - Py)
f5 = Rx * Qx - N
G = Ideal([f1, f2, f3, f4, f5]).groebner_basis()
#结式+矩阵子式(西尔维斯特矩阵)
print('[!] computing resultant h1...')
h1 = resultant(G[0], G[1], Rx) # Ry, Qx, Qy
print('[!] computing resultant h2...')
h2 = resultant(G[0], G[2], Rx) # Ry, Qx, Qy
print('[!] computing resultant h3...')
h3 = resultant(G[3], G[4], Rx) # Ry, Qx, Qy
print('[!] computing resultant h4...')
h4 = resultant(G[3], G[5], Rx) # Ry, Qx, Qy
print('[!] computing resultant h5...')
h5 = resultant(h1, h2, Ry) # Qx, Qy
print('[!] computing resultant h6...')
h6 = resultant(h3, h4, Ry) # Qx, Qy
print('[!] computing resultant h7...')
h7 = resultant(h5, h6, Qy) # Qx
print('[!] computing resultant h8...')
h8 = resultant(h7, f5, Qx) # Rx
roots = h8.univariate_polynomial().roots()
p, q = [ZZ(t[0]) for t in roots if ZZ(t[0]).is_prime()]Diffie-Hellman密钥交换(DH密钥交换 / DHKE)

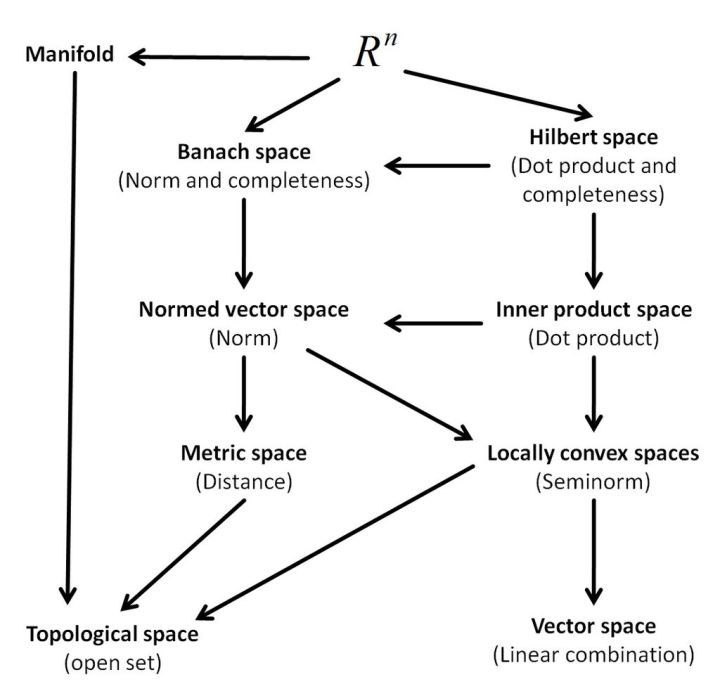
矩阵快速幂

int qpow(int x, int n, int m) {
int res = 1;
while (n) {
if (n & 1)
res = res * x % m;
x = x * x % m;
n >>= 1;
}
return res;
}根据矩阵乘法运算改写为矩阵快速幂:
#include <iostream>
using namespace std;
#define N 2
struct matrix {
int m[N][N];
matrix() {
memset(m, 0, sizeof(m));
}
void prt();
};
void matrix::prt() {
for (int i = 0; i < N; ++ i) {
for (int j = 0; j < N; ++ j) {
cout << this -> m[i][j] << " ";
}
cout << endl;
}
}
matrix operator * (const matrix a, const matrix b) {
matrix ans;
for (int i = 0; i < N; ++ i) {
for (int j = 0; j < N; ++ j) {
for(int k = 0; k < N; ++ k) {
ans.m[i][j] += a.m[i][k] * b.m[k][j];
}
}
}
return ans;
}
matrix qpow(matrix x, int n) {
matrix res;
for (int i = 0; i < N; ++ i) {
res.m[i][i] = 1;
}
while (n) {
if (n & 1) res = res * x;
x = x * x;
n >>= 1;
}
return res;
}
int fib(int n) {
matrix a;
a.m[0][0] = a.m[1][0] = a.m[0][1] = 1;
matrix base;
base.m[0][0] = 1;
matrix ans = qpow(a, n - 1);
ans = ans * base;
return ans.m[0][0];
}
int main() {
cout << fib(1) << endl; // 1
cout << fib(2) << endl; // 1
cout << fib(3) << endl; // 2
cout << fib(4) << endl; // 3
cout << fib(5) << endl; // 5
cout << fib(6) << endl; // 8
cout << fib(7) << endl; // 13
}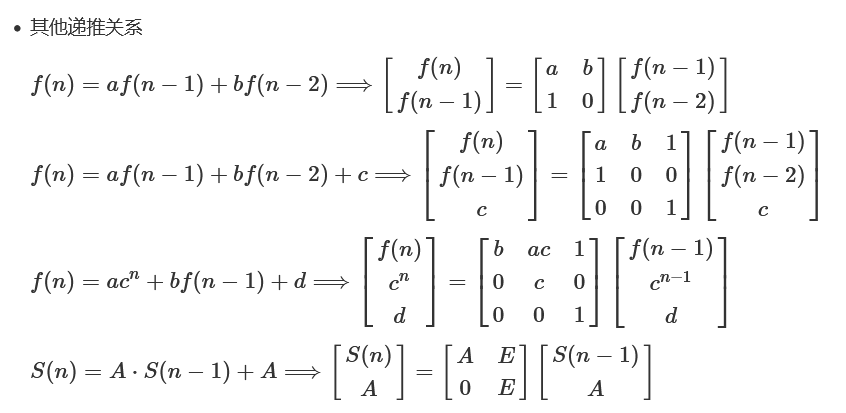
#以2x2矩阵相乘为例
m = [[1 for i in range(2)]for j in range(2)]
m[1][1] = 0
n = int(input())
def mulMatrix(x,y): #定义二阶矩阵相乘的函数
ans = [[0 for i in range(2)]for j in range(2)]
for i in range(2):
for j in range(2):
for k in range(2):
ans[i][j] += x[i][k] * y[k][j]
return ans
def quickMatrix(m,n):
E = [[0 for i in range(2)]for j in range(2)] #先定义一个单位矩阵
for i in range(2):
E[i][i] = 1
while(n):
if n % 2 != 0:
E = mulMatrix(E,m)
m = mulMatrix(m,m)
n >>= 1
return E
print(quickMatrix(m,n))佩尔方程 / Pell方程

def solve_pell(N, numTry = 100):
cf = continued_fraction(sqrt(N))
for i in range(numTry):
denom = cf.denominator(i)
numer = cf.numerator(i)
if numer^2 - N * denom^2 == 1:
return numer, denom
return None, None
N =
solve_pell(N)GM(Goldwasser-Micali)同态加密

from Crypto.Util.number import long_to_bytes
import gmpy2
plaintext = ''
with open('output.txt') as f:
n = int(f.readline())
for line in f:
cipher = int(line)
if gmpy2.jacobi(cipher,n) == -1:
plaintext += '1'
else:
plaintext += '0'
print(long_to_bytes(int(plaintext,2)))ElGamal加密

Paillier同态加密

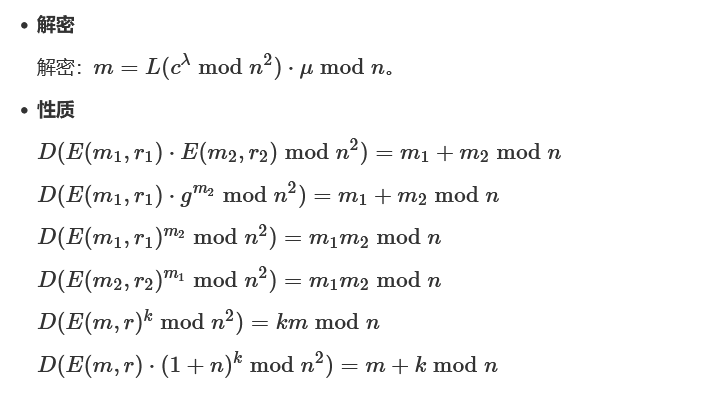
Merkle-Hellman背包加密(Knapsack)


参考:Lattice Reduction Attack on the Knapsack Type Cryptosystem
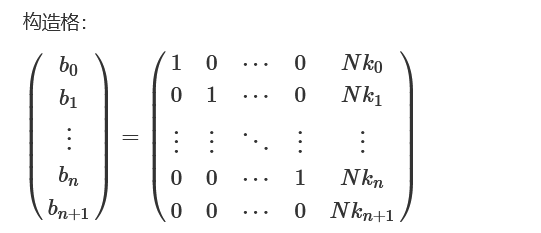
M = Matrix.identity(n)
last_row = [0 for x in keys]
M_last_row = Matrix(ZZ, 1, len(last_row), last_row)
ct =
last_col = keys[:]
last_col.append(ct)
M_last_col = Matrix(ZZ, len(last_col), 1, last_col)
M = M.stack(M_last_row)
M = M.augment(M_last_col)
X = M.LLL()
target = X[0][:-1]
ans = [-k for k in target]对于密度比较高的Knapsack密码系统,在1的数量确定情况下,可以尝试分段爆破。
参考论文:Improved Generic Algorithms for Hard Knapsacks
常规解密脚本
from sage.all import *
pk = # public key
ct = # ciphertext
print(ct)
print(len(pk))
n = len(pk)
# Sanity check for application of low density attack
d = n / log(max(pk), 2)
print(CDF(d))
assert CDF(d) < 0.9408
M = Matrix.identity(n) * 2
last_row = [1 for x in pk]
M_last_row = Matrix(ZZ, 1, len(last_row), last_row)
last_col = pk
last_col.append(ct)
M_last_col = Matrix(ZZ, len(last_col), 1, last_col)
M = M.stack(M_last_row)
M = M.augment(M_last_col)
X = M.BKZ()
sol = []
for i in range(n + 1):
testrow = X.row(i).list()[:-1]
if set(testrow).issubset([-1, 1]):
for v in testrow:
if v == 1:
sol.append(0)
elif v == -1:
sol.append(1)
break
s = sol
print(s)泄露部分明文空间的降维处理
###Sage
pubkey = [...]
c =
#前缀 flag{
prefix = [int(_) for _ in bin(bytes_to_long(b'flag{'))[2:]]
for i in range(len(prefix)):
c -= prefix[i] * pubkey[i]
#后缀 }
suffix = [int(_) for _ in bin(ord('}'))[2:].rjust(8, '0')]
n = len(pubkey)
for i in range(8):
c -= pubkey[n - 8 + i] * suffix[i]
#中部md5范围 0-f
elements = []
for i in range(len(prefix), len(pubkey) - 8, 8):
elements.append(pubkey[i + 1])
c -= 1 * pubkey[i + 2]
for j in range(3, 8):
elements.append(pubkey[i + j])
n = len(elements)
A = Matrix(ZZ, n + 1, n + 1)
for i in range(n):
A[i, 0] = elements[i]
A[i, i + 1] = 2
A[n, 0] = c
for i in range(1, n + 1):
A[n, i] = 1
AL = A.BKZ()
mid = None
for line in AL:
if all(line[i] == 1 or line[i] == -1 for i in range(1, n + 1)):
if line[1] == 1:
line = -line
mid = line[1:]
break
mid_str = ''
for _ in mid:
if _ == -1:
mid_str += '0'
else:
mid_str += '1'
flag = ''
j = 0
for i in range(32):
flag += '0'
flag += mid_str[j]
j += 1
flag += '1'
for k in range(5):
flag += mid_str[j]
j += 1
print(bytes.fromhex(hex(int(flag, 2))[2:]))-
子集合问题 转化为 求解SVP/CVP+Lattice Reduction Algorithm
参考:
Crypto Research: Solving Subset Sum Problem by Lattice Reduction
import re
import random
import multiprocessing as mp
from functools import partial
def check(sol, A, s):
"""Check whether *sol* is a solution to the subset-sum problem.
"""
return sum(x*a for x, a in zip(sol, A)) == s
def solve(A, n, k, s, ID=None, BS=22):
N = ceil(sqrt(n)) # parameter used in the construction of lattice
rand = random.Random(x=ID) # seed
# 1. Construct the lattice
# (n+1) * (n+2)
# 1 0 ... 0 a_0*N N
# 0 1 ... 0 a_1*N N
# . . ... . ... .
# 0 0 ... 1 a_n*N N
# 0 0 ... 0 s*N k*N
lat = []
for i, a in enumerate(A):
lat.append([1*(j == i) for j in range(n)] + [N*a] + [N])
lat.append([0]*n + [N*s] + [k*N])
# main loop
itr = 0
start_time = cputime()
while True:
itr += 1
# 2. Randomly shuffle
l = lat[::]
shuffle(l, random=rand.random)
# 3. BKZ!!!
m = matrix(ZZ, l)
t_BKZ = cputime()
m_BKZ = m.BKZ(block_size=BS)
print(f"n={n} {itr} runs. BKZ running time: {cputime(t_BKZ):.3f}s")
# 4. Check the result
for i, row in enumerate(m_BKZ):
if check(row, A, s):
if row.norm()^2 == k:
print(f"n={n} After {itr} runs. FIND SVP!!! {row}\n"
f"Single core time used: {cputime(start_time):.3f}s")
return True
s =
A = []
#choose k numbers from n
k =
n =
solve_n = partial(solve, A, n, k, s)
CPU_CORE_NUM = 8
with mp.Pool(CPU_CORE_NUM) as pool:
reslist = pool.imap_unordered(solve_n, range(CPU_CORE_NUM))
# terminate all processes once one process returns
for res in reslist:
if res:
pool.terminate()
breakBenaloh加密

https://mystiz.hk/posts/2021-02-15-dicectf-1/
from Crypto.Util.number import long_to_bytes
from tqdm import tqdm
n =
y =
e =
C = []
p =
q =
phi = (p-1) * (q-1)
tmp = phi // e
bounds = (1, e)
F = IntegerModRing(n)
result = []
x = F(pow(y, tmp, n))
for c in tqdm(C):
a = F(pow(c, tmp, n))
result.append(bsgs(x, a, bounds))
flag = 0
for i in result[::-1]:
flag = flag*e + i
flag = long_to_bytes(flag)
print(flag)LUC-RSA加密


LUC-RSA:
A new attack on three variants of the RSA cryptosystem
Cryptanalysis of RSA-type cryptosystems based on Lucas sequences, Gaussian integers and elliptic curves
#法1,快速矩阵幂
from Crypto.Util.number import long_to_bytes
N=
C=
def ffm(num): # Fermat's Factorization Method.
if num%2==0: return (2,num/2)
a=ceil(sqrt(num))
c=a**2-num
while is_square(c)==0: a+=1
b=sqrt(c)
return (a-b,a+b)
def matpow(mat,power): # Matrix Square-And-Multiply Exponentiation.
power_rep=bin(power)[3:]
result=mat
pcnt=1
for i in power_rep:
result=result*result
pcnt*=2
if i=='1':
result=mat*result
pcnt+=1
print(pcnt)
return result
def decrypt(d): # Decryption.
Mat=Matrix(Zmod(N),[[C,-1],[1,0]])
ori=vector(Zmod(N),[C,2])
return matpow(Mat,d-1)*ori
p,q=ffm(N)
assert p*q==N
D=(C**2-4)%N
p_leg,q_leg=int((p-kronecker(D,p))%N),int((q-kronecker(D,q))%N)
tn=lcm((p_leg),(q_leg))
d=inverse_mod(0x10001,tn)
assert (0x10001*d)%tn==1
decc,_=decrypt(d)
print(long_to_bytes(decc))#法2,存储vd
#vd(2n)=vd(n)^2-2
#vd(2n+1)=c*vd(n)^2-vd(n)*vd(n-1)+c
def v(n):
if n == 0: return 2
if n == 1: return c
if n in v_dict.keys(): return v_dict[n]
if(n % 2 == 0): ret = (pow(v(n // 2), 2, N) - 2) % N
else: ret = (c * pow(v(n // 2), 2, N) - v(n // 2) * v((n // 2) - 1) - c) % N
v_dict[n] = ret
return ret#法3,William's p+1算法优化vd
# Williams's p + 1 algorithm
def LUC(c, d, N):
x = c
y = (c**2 - 2) % N
for bit in bin(d)[3:]:
if bit == '1':
x = (x*y - c) % N
y = (y**2 - 2) % N
else:
y = (x*y - c) % N
x = (x**2 - 2) % N
return xDSA数字签名


参考:Recovering cryptographic keys from partial information, by example
Elgamal数字签名


Shamir密钥分享算法

#python-1
from sslib import shamir
data = {'required_shares': 2, 'prime_mod': 'AQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEp', 'shares': ['1-MEwx7cz+C01rL8H0Hhz2EIgHjWYXVcL81uITmRha674=', '2-YJhj22+ntS1s80CT9b6Y7ayc52baTFGNRpPUyLxtaf8=', '3-4SRZDcshiZTVRJ7nVY8NDq83JOsnZtPm', '4-wTDHtrT7CO1wej3TpQHep/XHm2hgOW6uJfdXKASSZoE=', '5-8Xz5pFekss1yPbxzfKOBhRpc9WkjL/0+lakYV6ik5MI=']}
print(shamir.recover_secret(shamir.from_base64(data)).decode('ascii'))#python-2
from Crypto.Util.number import *
import gmpy2
def product(vals, p):
return reduce(lambda x, y: x * y % p, vals)
def lagrange_interpolate(x, x_s, y_s, p):
n = len(x_s)
assert n == len(set(x_s)) # x_s must be distinct
num = []
den = []
for i in range(n):
others = x_s[:i] + x_s[i+1:]
num.append(product((x - o for o in others), p))
den.append(product((x_s[i] - o for o in others), p))
dens = product(den, p)
res = 0
for i in range(n):
tmp1 = ((num[i] * dens % p) * y_s[i]) % p
tmp2 = tmp1 * gmpy2.invert(den[i], p) % p
res = (res + tmp2) % p
res = res * gmpy2.invert(dens, p) % p
return res
def shamir_sharing_encode(s, k, n, p):
a = [getRandomInteger(Nbits) for _ in range(k-1)]
res = []
for _ in range(n):
x = getRandomInteger(Nbits)
fx = s
for i in range(k-1):
fx = (fx + a[i] * pow(x, i+1, p)) % p
res.append((x, fx))
return res
def shamir_sharing_decode(shares, p):
x_s, y_s = zip(*shares)
return lagrange_interpolate(0, x_s, y_s, p)
Nbits = 1024
secret = bytes_to_long('it_is_the_top_secret')
p = getPrime(Nbits)
k = 513
n = 513
shares = shamir_sharing_encode(secret, k, n, p)
s = shamir_sharing_decode(shares, p)
print long_to_bytes(s)
# 2s#Sage
P = PolynomialRing(GF(p), 'x')
ret = P(0)
for x, y in shares:
r = P(1) * y
for xx, yy in shares:
if x != xx:
r = r * P((0 - xx) / (x - xx))
ret = ret + r
print ret
# 19s
#Sage算系数
P = PolynomialRing(GF(p), 'x')
ret = P(0)
for x, y in shares:
r = P(1) * y
for xx, yy in shares:
if x != xx:
r = r * P('(x - %d) / (%d - %d)' % (xx, x, xx))
ret = ret + r
print ret[0]
# 154s
#Sage矩阵乘法
k = 513
n = 513
x, y = zip(*shares)
array_1 = []
for i in range(n):
for j in range(k):
array_1.append(pow(x[i], j, p))
A = matrix(GF(p), n, k, array_1)
array_2 = []
for i in range(n):
array_2.append(y[i])
B = matrix(GF(p), n, 1, array_2)
a = A.solve_right(B)
print a[0][0]
# 266s
#Sage
fx_num = 513
x, y = zip(*shares)
array_1 = []
for i in range(fx_num):
for j in range(fx_num):
array_1.append(pow(x[i], j, p))
delta = matrix(GF(p), fx_num, fx_num, array_1).determinant()
array_2 = [_ for _ in array_1]
for i in range(fx_num):
array_2[i*fx_num] = y[i]
delta_0 = matrix(GF(p), fx_num, fx_num, array_2).determinant() % p
delta_inverse = inverse_mod(int(delta), p)
res = delta_inverse * delta_0 % p
print res
# 1200s
#Sage
fx_num = 513
x, y = zip(*shares)
delta = 1
for i in range(1, fx_num):
for j in range(0, i):
t = x[i] - x[j]
delta = (delta * t) % p
delta_0 = 0
for i in range(fx_num):
tmp_x = [_ for _ in x]
tmp_x.pop(i)
yuzishi = -y[i] if (i+1+1) % 2 else y[i]
for j in range(fx_num-1):
yuzishi = (yuzishi * tmp_x[j]) % p
for j in range(1, fx_num-1):
for k in range(0, j):
t = tmp_x[j] - tmp_x[k]
yuzishi = (yuzishi * t) % p
delta_0 = (delta_0 + yuzishi) % p
delta_inverse = gmpy2.invert(delta, p)
res = delta_inverse * delta_0 % p
print res
# 224s
#Sage
a = 99999999
b = 123456
PR.<s1,s2,A> = PolynomialRing(Zmod(p))
f1 = s1 + A - y1
f2 = s2 + A - y2
f3 = a * s1 + b - s2
Fs = [f1, f2, f3]
I = Ideal(Fs)
B = I.groebner_basis()
print 's1 =', ZZ(-B[0](0, 0, 0))
print 's2 =', ZZ(-B[1](0, 0, 0))Okamoto-Uchiyama密码系统


参考:PoseidonCTF 1st Edition 2020 - discrete log
Schmidt-Samoa密码系统


参考:A New Rabin-type Trapdoor Permutation Equivalent to Factoring and Its Applications


 浙公网安备 33010602011771号
浙公网安备 33010602011771号