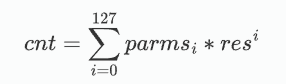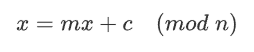2023第十四届极客大挑战 — CRYPTO(WP全)
浅谈:
本次大挑战我们队伍也是取得了第一名的成绩,首先要感谢同伴的陪伴和帮助。在共同的努力下终不负期望!
但遗憾的是我们没有在某个方向全通关的,呜呜呜~ 继续努力吧!要学的还很多。明年有机会再战!!加油!
Crypto方向题解:来自本人
第一波题目
SignIn
1、题目信息
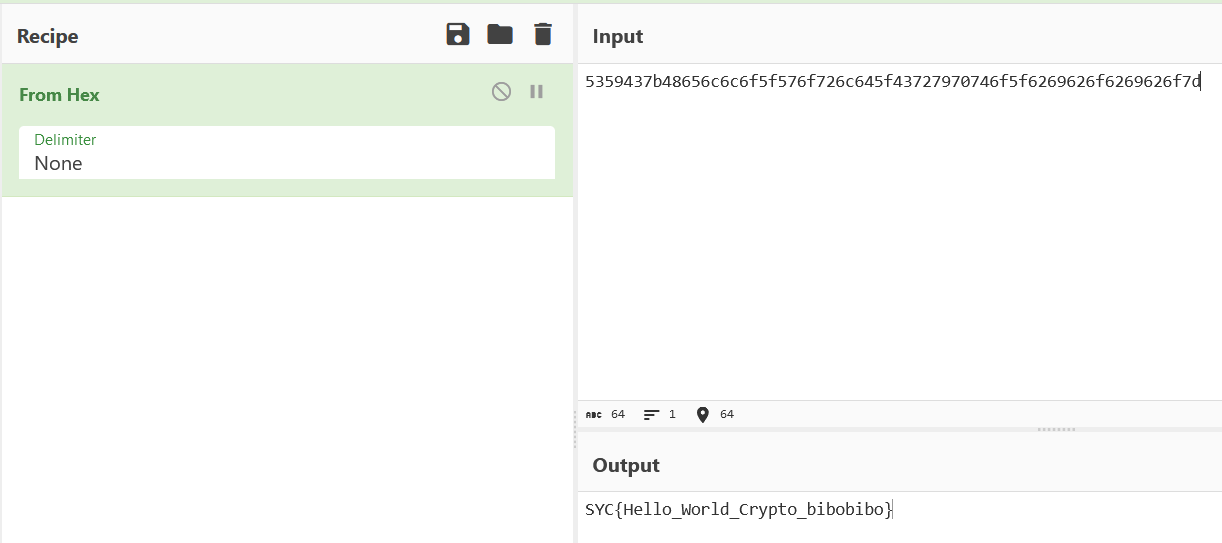
Bibo...Hello! 你好! こんにちは! Привет! 5359437b48656c6c6f5f576f726c645f43727970746f5f6269626f6269626f7d… Hmm... Something goes wrong with my grettings bot. 2、解题方法
看到HEX编码
5359437b48656c6c6f5f576f726c645f43727970746f5f6269626f6269626f7d直接解
proof_of_work
1、题目信息
题目链接:nc ... Build your own function to solve proof_of_work!2、解题方法
连接靶机得到
sha256(XXXX+YMBlFIGoaFZ1Z24P) == 77aeea7731a49f8bc37099419177dc7b51d8941a4c7213c76ad7b4466f35f050
Give me XXXX:缺少前四位,哈希碰撞,简单的
exp:
import hashlib
dic = 'abcdefghijklmnopqrstuvwxyz1234567890ABCDEFGHIJKLMNOPQRSTUVWXYZ'
for a in dic:
for b in dic:
for c in dic:
for d in dic:
t =str(a)+str(b)+str(c)+str(d)+'YMBlFIGoaFZ1Z24P'
m = (hashlib.sha256(t.encode())).hexdigest()
if m[:64] == '77aeea7731a49f8bc37099419177dc7b51d8941a4c7213c76ad7b4466f35f050':
print(t)
breakeri8YMBlFIGoaFZ1Z24P输入即可
Right!
Congrats! Your flag is: SYC{st3p_1nt0_1nter4ctive_Crypt0graphy}SimpleRSA
1、题目信息
So simple RSA! Wait... Are you kidding me? https://en.wikipedia.org/wiki/RSA_(cryptosystem)import gmpy2
from Crypto.Util.number import *
flag = b"SYC{Al3XEI_FAKE_FLAG}"
assert len(flag) == 35
p,q = [getPrime(2048) for _ in "__"]
n = p*q
e = 65537
c = gmpy2.powmod(bytes_to_long(flag),e,n)
print(p)
print(c)
#24724324630507415330944861660078769085865178656494256140070836181271808964994457686409910764936630391300708451701526900994412268365698217113884698394658886249353179639767806926527103624836198494439742123128823109527320850165486500517304731554371680236789357527395416607541627295126502440202040826686102479225702795427693781581584928770373613126894936500089282093366117940069743670997994742595407158340397268147325612840109162997306902492023078425623839297511182053658542877738887677835528624045235391227122453939459585542485427063193993069301141720316104612551340923656979591045138487394366671477460626997125944456537
#5103456617184503756323047648197242238240186093599642595037622832533500101615151909121526236040190932669670958473343882813904068315876632531642565439056940219522112206528202255274138612084527602157678289270398934355285721482825291987737728642550612132082799990111949521463627484851030321498065381406935373617552101766988951047083794008065119077199048670688659702412088066150610550472540261180168367502839664781039873753618261989305294622610133249045220148045025828657164418288950475500414011721271297499695078533555311978149196039636646462205056723025430859593726793957178920602454614648615071642764421404073088325377074507294322241507546035185262887671056823991904386800859250780514594486187258712495630118645255858701881237255544116550441529948260569005022987728021335265917943282249324056805837573070643957923173835718666195829743773447369302715541607014783857634260910916864967889995883404192267852170285046845421979703879162621262789552785234529030433164528257380306451002715959426524988525066607896058463096023439322454354214256730582387855092803662297544049492196630436274314377550878555021398906394684819227889738217839577664338577737712292983280192506526252897009501654145849834873190780905731794708934506324194671111173414722、解题方法
给出p, c, e, 而且p,q是循环生成的两个大素数,本身flag较短。利用公式
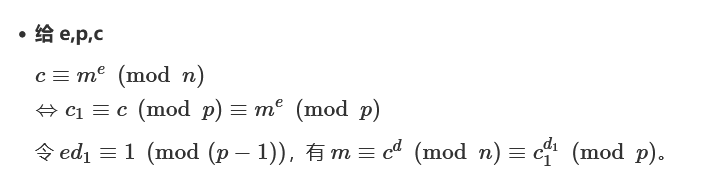
exp:
import gmpy2
from Crypto.Util.number import long_to_bytes
e = 65537
p = 24724324630507415330944861660078769085865178656494256140070836181271808964994457686409910764936630391300708451701526900994412268365698217113884698394658886249353179639767806926527103624836198494439742123128823109527320850165486500517304731554371680236789357527395416607541627295126502440202040826686102479225702795427693781581584928770373613126894936500089282093366117940069743670997994742595407158340397268147325612840109162997306902492023078425623839297511182053658542877738887677835528624045235391227122453939459585542485427063193993069301141720316104612551340923656979591045138487394366671477460626997125944456537
c = 510345661718450375632304764819724223824018609359964259503762283253350010161515190912152623604019093266967095847334388281390406831587663253164256543905694021952211220652820225527413861208452760215767828927039893435528572148282529198773772864255061213208279999011194952146362748485103032149806538140693537361755210176698895104708379400806511907719904867068865970241208806615061055047254026118016836750283966478103987375361826198930529462261013324904522014804502582865716441828895047550041401172127129749969507853355531197814919603963664646220505672302543085959372679395717892060245461464861507164276442140407308832537707450729432224150754603518526288767105682399190438680085925078051459448618725871249563011864525585870188123725554411655044152994826056900502298772802133526591794328224932405680583757307064395792317383571866619582974377344736930271554160701478385763426091091686496788999588340419226785217028504684542197970387916262126278955278523452903043316452825738030645100271595942652498852506660789605846309602343932245435421425673058238785509280366229754404949219663043627431437755087855502139890639468481922788973821783957766433857773771229298328019250652625289700950165414584983487319078090573179470893450632419467111117341472
c1 = gmpy2.powmod(c,1,p)
#print(c1)
c1 = 4051214058804479368392672378735549121098858914222376579437253801094236077441467676514581111652283758229424464184778957984747437311884228390302136410558148974712344908234510044660168367785415961415047536214954790311033443902257586441153728895997584348202577220497738797942324111995037096097268934053788741967582039722075276514285656939591558765835657643982917853435078915341605460540295941943954509346184797648297092833816943277070377424440376503265230008537496494495338735818373418662569818535110895085066183097198245782175273695234075807560220916970685214729061789487329680664087145876085675558053582127109983793698
d1 = gmpy2.invert(e,(p-1))
m = gmpy2.powmod(c1,d1,p)
print(long_to_bytes(m))
#SYC{Just_a_s1mple_modular_equation}OTPTwice
1、题目信息
I invented a new symmetric cryptosystem, and I believe you will never break it! from pwn import xor
from os import urandom
flag = b"SYC{Al3XEI_FAKE_FLAG}"
# step0: key generation & distribution
def s0(msg):
k1,k2 = [urandom(len(msg)) for _ in "__"]
return k1,k2
#
# step1: Alice encrypt M, and send it to Bob
def s1(msg,k1):
c1 = xor(msg,k1)
return c1
# step2: Bob encrypt c1, and send it to Alice
def s2(msg,k2):
c2 = xor(msg,k2)
return c2
# step3: Alice decrypt c2, and send it to Bob.
def s3(msg,k1):
c3 = xor(msg,k1)
return c3
# step4: Bob decrypt c3, get M.
def s4(msg,k2):
m_ = xor(msg,k2)
return m_
def encrypt(msg,k1,k2):
c1 = s1(msg,k1)
c2 = s2(c1,k2)
c3 = s3(c2,k1)
m_ = s4(c3,k2)
assert msg == m_
# Here's what hacker Eve got:
def encrypt_(msg,k1,k2):
c1 = s1(msg,k1)
c2 = s2(c1,k2)
c3 = s3(c2,k1)
m_ = s4(c3,k2)
if HACK == True:
print(c1)
print(c2)
print(c3)
k1,k2 = s0(flag)
encrypt_(flag,k1,k2)
'''
b'\xdbi\xab\x8d\xfb0\xd3\xfe!\xf8Xpy\x80w\x8c\x87\xb9'
b'o\xb0%\xfb\xdb\x0e\r\x04\xde\xd1\x9a\x08w\xda4\x0f\x0cR'
b'\xe7\x80\xcd\ria\xb2\xca\x89\x1a\x9d;|#3\xf7\xbb\x96'
'''2、解题方法
简单分析一下,异或、逆向思维,不难看出我们需要求出k1,k1就是我们的flag
exp:
from pwn import xor
from os import urandom
# 已知的消息和密钥
flag = b"SYC{Al3XEI_FAKE_FLAG}"
c1 = b'\xdbi\xab\x8d\xfb0\xd3\xfe!\xf8Xpy\x80w\x8c\x87\xb9'
c2 = b'o\xb0%\xfb\xdb\x0e\r\x04\xde\xd1\x9a\x08w\xda4\x0f\x0cR'
c3 = b'\xe7\x80\xcd\ria\xb2\xca\x89\x1a\x9d;|#3\xf7\xbb\x96'
m_ = flag # 已知的原始消息
# 将十六进制的加密消息转换为二进制
c1_bin = bytes.fromhex(c1.hex())
c2_bin = bytes.fromhex(c2.hex())
c3_bin = bytes.fromhex(c3.hex())
# 使用XOR操作推导出密钥k1
k1 = xor(c2, c1) # c2 = xor(c1, k1), 所以 k1 = xor(c2, c1)
k1 = xor(k1, c3) # c3 = xor(c2, k1), 所以 k1 = xor(k1, c3)
# 将二进制密钥转换为十六进制格式
k1_hex = k1.hex()
print("推导出的密钥k1 (十六进制格式):", k1_hex)
print("推导出的密钥k1 :", k1)推导出的密钥k1 (十六进制格式): 5359437b495f6c3076335f4372797074307d
推导出的密钥k1 : b'SYC{I_l0v3_Crypt0}'OldAlgorithm
1、题目信息
An old algorithm but widely used nowadays.from Crypto.Util.number import *
import os
flag = b"SYC{Al3XEI_FAKE_FLAG}"
pad = lambda msg,padlen: msg+os.urandom(padlen-len(msg))
flag = pad(flag,32)
print(len(flag))
p = [getPrime(16) for _ in range(32)]
c = [bytes_to_long(flag)%i for i in p]
print('p=',p)
print('c=',c)
'''
p= [58657, 47093, 47963, 41213, 57653, 56923, 41809, 49639, 44417, 38639, 39857, 53609, 55621, 41729, 60497, 44647, 39703, 55117, 44111, 57131, 37747, 63419, 63703, 64007, 46349, 39241, 39313, 44909, 40763, 46727, 34057, 56333]
c= [36086, 4005, 3350, 23179, 34246, 5145, 32490, 16348, 13001, 13628, 7742, 46317, 50824, 23718, 32995, 7640, 10590, 46897, 39245, 16633, 31488, 36547, 42136, 52782, 31929, 34747, 29026, 18748, 6634, 9700, 8126, 5197]
'''一眼丁真,中国剩余定理。参考:中国剩余定理(孙子定理 / CRT)
exp:
参考文章里面脚本拿来直接用,sage跑出m即可。
#sage
#仅适用模两两互素
def chinese_remainder(modulus, remainders):
Sum = 0
prod = reduce(lambda a, b: a*b, modulus)
for m_i, r_i in zip(modulus, remainders):
p = prod // m_i
Sum += r_i * (inverse_mod(p,m_i)*p)
return Sum % prod
chinese_remainder([58657, 47093, 47963, 41213, 57653, 56923, 41809, 49639, 44417, 38639, 39857, 53609, 55621, 41729, 60497, 44647, 39703, 55117, 44111, 57131, 37747, 63419, 63703, 64007, 46349, 39241, 39313, 44909, 40763, 46727, 34057, 56333]
,[36086, 4005, 3350, 23179, 34246, 5145, 32490, 16348, 13001, 13628, 7742, 46317, 50824, 23718, 32995, 7640, 10590, 46897, 39245, 16633, 31488, 36547, 42136, 52782, 31929, 34747, 29026, 18748, 6634, 9700, 8126, 5197]
)
#37699681561344853433172597523387281471904607566697320008840601281159457436694import gmpy2
from Crypto.Util.number import long_to_bytes
m = 37699681561344853433172597523387281471904607566697320008840601281159457436694
print(long_to_bytes(m))
#SYC{CRT_1s_s0_ju1cy!}easy_classic
1、题目信息
非常好套娃,使我的古典旋转 
2、解题方法
这个题感觉是最有意思的。。。每层都有提示和压缩包,需要逐步分析每层,而且提示文件并没给出具体是什么密码
这就单纯考察我们对古典密码的熟练程度了。。。一 一 破解吧。哎!!!古典。
第一步:凯撒密码
udzeojxuwqcu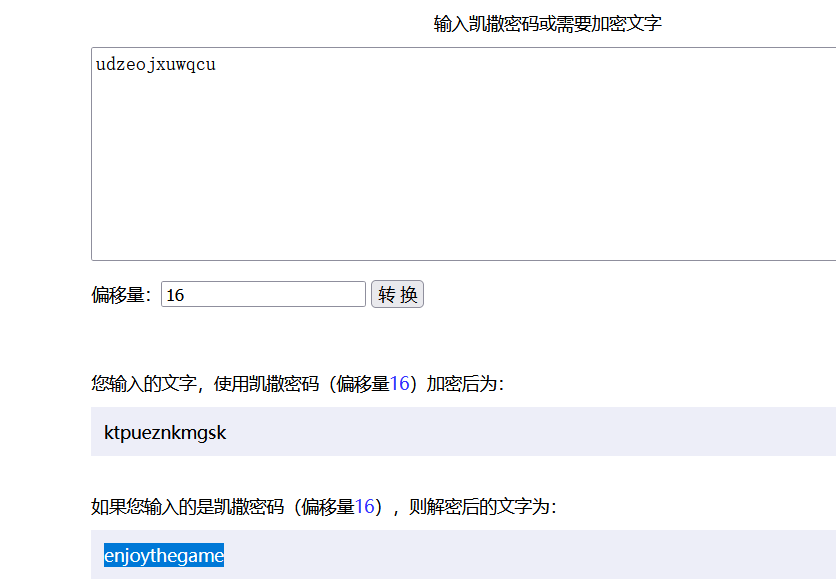
第二步:W型栏栅
ialhhooavtepcyr随波逐流工具解得
分为7栏时,解密结果为:ilovecryptohaha第三步:base64
5a6H5a6Z5LiH5rOV55qE6YKj5Liq5rqQ5aS0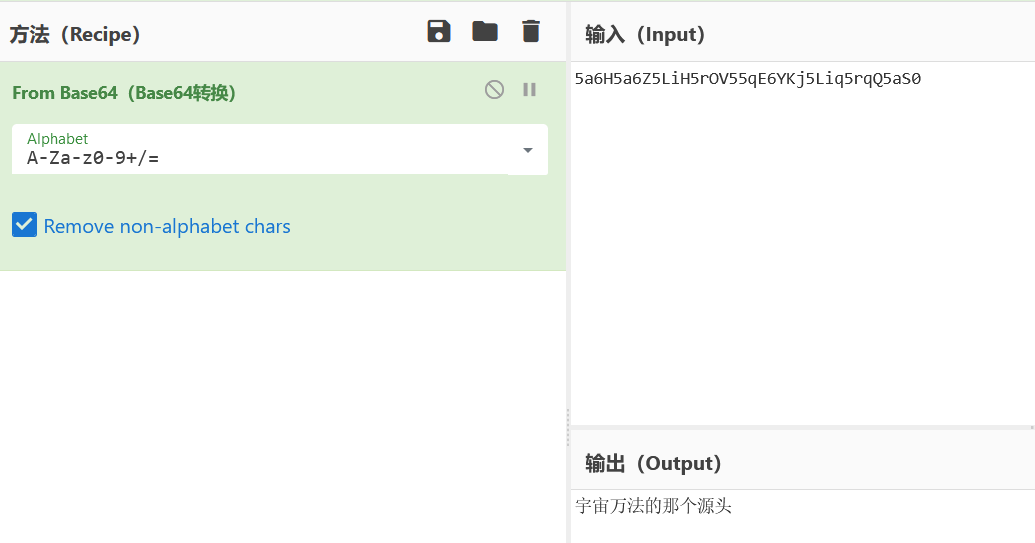
第四步:熊曰
熊曰:呋食食食取噗山笨笨破嗄咯哈動嗡雜類嗒嘿啽沒歡破吖咬我啽寶盜噔咯沒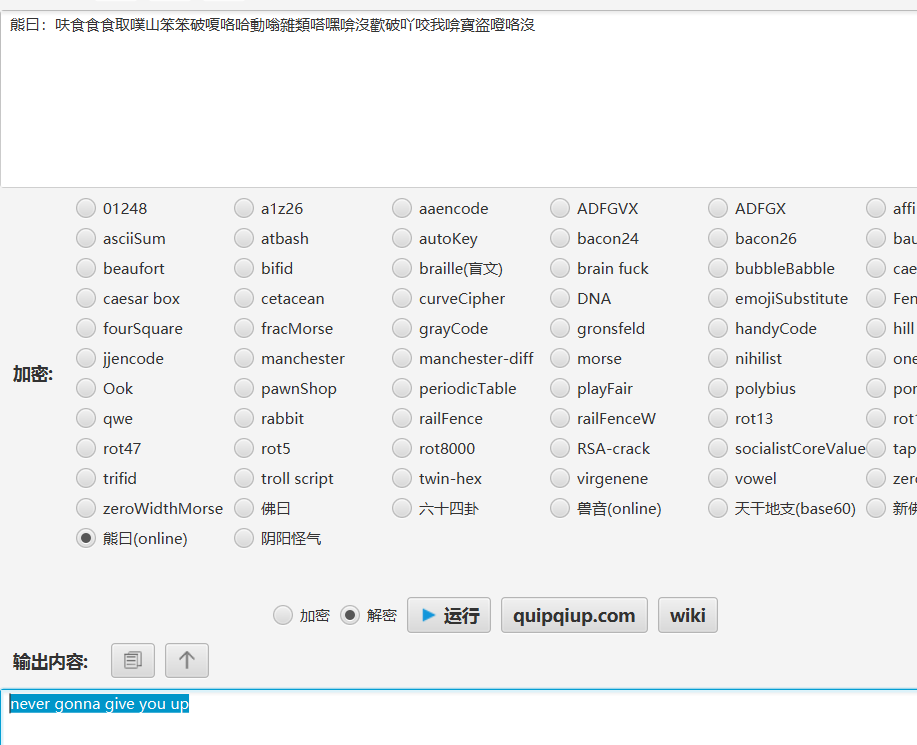
第五步:base100+普莱菲尔密码
password: adltlfltqrcy
key: 👝👘👠👩👞👘👤👜先base100解出key
fairgame再普莱
最后拿到flag
SYC{classical_1s_fun}第二波题目
PolyRSA
题目信息
Harder RSA. Check it out!
附件信息
import gmpy2
from Crypto.Util.number import *
flag = b"SYC{Al3XEI_FAKE_FLAG}"
p,q = [getPrime(2048) for _ in "__"]
e1,e2 = [getPrime(17) for _ in "__"]
e = 65537
n = p*q
c1 = gmpy2.powmod(2*p + 3*q,e1,n)
c2 = gmpy2.powmod(5*p + 7*q,e2,n)
c = gmpy2.powmod(bytes_to_long(flag),e,n)
print("e1=",e1)
print("e2=",e2)
print("c1=",c1)
print("c2=",c2)
print("c=",c)
print("n=",n)
#e1= 113717
#e2= 80737
#c1= 97528398828294138945371018405777243725957112272614466238005409057342884425132214761228537249844134865481148636534134025535106624840957740753950100180978607132333109806554009969378392835952544552269685553539656827070349532458156758965322477969141073720173165958341043159560928836304172136610929023123638981560836183245954461041167802574206323129671965436040047358250847178930436773249800969192016749684095882580749559014647942135761757750292281205876241566597813517452803933496218995755905344070203047797893640399372627351254542342772576533524820435965479881620338366838326652599102311019884528903481310690767832417584600334987458835108576322111553947045733143836419313427495888019352323209000292825566986863770366023326755116931788018138432898323148059980463407567431417724940484236335082696026821105627826117901730695680967455710434307270501190258033004471156993017301443803372029004817834317756597444195146024630164820841200575179112295902020141040090350486764038633257871003899386340004440642516190842086462237559715130631205046041819931656962904630367121414263911179041905140516402771368603623318492074423223885367923228718341206283572152570049573607906130786276734660847733952210105659707746969830132429975090175091281363770357
#c2= 353128571201645377052005694809874806643786163076931670184196149901625274899734977100920488129375537186771931435883114557320913415191396857882995726660784707377672210953334914418470453787964899846194872721616628198368241044602144880543115393715025896206210152190007408112767478800650578941849344868081146624444817544806046188600685873402369145450593575618922226415069043442295774369567389939040265656574664538667552522329712111984168798829635080641332045614585247317991581514218486004191829362787750803153463482021229058714990823658655863245025037102127138472397462755776598314247771125981017814912049441827643898478473451005083533693951329544115861795587564408860828213753948427321483082041546722974666875065831843384005041800692983406353922680299538080900818930589336142421748023025830846906503542594380663429947801329079870530727382679634952272644949425079242992486832995962516376820051495641486546631849426876810933393153871774796182078367277299340503872124124714036499367887886486264658590613431293656417255355575602576047502506125375605713228912611320198066713358654181533335650785578352716562937038768171269136647529849805172492594142026261051266577821582011917001752590659862613307646536049830151262848916867223615064832279222
#c= 375617816311787295279632219241669262704366237192565344884527300748210925539528834207344757670998995567820735715933908541800125317082581328287816628816752542104514363629022246620070560324071543077301256917337165566677142545053272381990573611757629429857842709092285442319141751484248315990593292618113678910350875156232952525787082482638460259354559904243062546518553607882194808191571131590524874275187750985821420412987586148770397073003186510357920710387377990379862185266175190503647626248057084923516190642292152259727446111686043531725993433395002330208067534104745851308178560234372373476331387737629284961288204368572750848248186692623500372605736825205759172773503283282321274793846281079650686871355211691681512637459986684769598186821524093789286661348936784712071312135814683041839882338235290487868969391040389837253093468883093296547473466050960563347060307256735803099039921213839491129726807647623542881247210251994139130146519265086673883077644185971830004165931626986486648581644383717994174627681147696341976767364316172091139507445131410662391699728189797082878876950386933926807186382619331901457205957462337191923354433435013338037399565519987793880572723211669459895193009710035003369626116024630678400746946356
#n= 728002565949733279371529990942440022467681592757835980552797682116929657292509059813629423038094227544032071413317330087468458736175902373398210691802243764786251764982802000867437756347830992118278032311046807282193498960587170291978547754942295932606784354258945168927044376692224049202979158068158842475322825884209352566494900083765571037783472505580851500043517614314755340168507097558967372661966013776090657685241689631615245294004694287660685274079979318342939473469143729494106686592347327776078649315612768988028622890242005700892937828732613800620455225438339852445425046832904615827786856105112781009995862999853122308496903885748394541643702103368974605177097553007573113536089894913967154637055293769061726082740854619536748297829779639633209710676774371525146758917646731487495135734759201537358734170552231657257498090553682791418003138924472103077035355223367678622115314235119493397080290540006942708439607767313672671274857069053688258983103863067394473084183472609906612056828326916114024662795812611685559034285371151973580240723680736227737324052391721149957542711415812665358477474058103338801398214688403784213100455466705770532894531602252798634923125974783427678469124261634518543957766622712661056594132089参考文章:
https://blog.csdn.net/weixin_44617902/article/details/112978062
exp:
#解密脚本:
import gmpy2
from Crypto.Util.number import long_to_bytes
e1= 113717
e2= 80737
c1= 97528398828294138945371018405777243725957112272614466238005409057342884425132214761228537249844134865481148636534134025535106624840957740753950100180978607132333109806554009969378392835952544552269685553539656827070349532458156758965322477969141073720173165958341043159560928836304172136610929023123638981560836183245954461041167802574206323129671965436040047358250847178930436773249800969192016749684095882580749559014647942135761757750292281205876241566597813517452803933496218995755905344070203047797893640399372627351254542342772576533524820435965479881620338366838326652599102311019884528903481310690767832417584600334987458835108576322111553947045733143836419313427495888019352323209000292825566986863770366023326755116931788018138432898323148059980463407567431417724940484236335082696026821105627826117901730695680967455710434307270501190258033004471156993017301443803372029004817834317756597444195146024630164820841200575179112295902020141040090350486764038633257871003899386340004440642516190842086462237559715130631205046041819931656962904630367121414263911179041905140516402771368603623318492074423223885367923228718341206283572152570049573607906130786276734660847733952210105659707746969830132429975090175091281363770357
c2= 353128571201645377052005694809874806643786163076931670184196149901625274899734977100920488129375537186771931435883114557320913415191396857882995726660784707377672210953334914418470453787964899846194872721616628198368241044602144880543115393715025896206210152190007408112767478800650578941849344868081146624444817544806046188600685873402369145450593575618922226415069043442295774369567389939040265656574664538667552522329712111984168798829635080641332045614585247317991581514218486004191829362787750803153463482021229058714990823658655863245025037102127138472397462755776598314247771125981017814912049441827643898478473451005083533693951329544115861795587564408860828213753948427321483082041546722974666875065831843384005041800692983406353922680299538080900818930589336142421748023025830846906503542594380663429947801329079870530727382679634952272644949425079242992486832995962516376820051495641486546631849426876810933393153871774796182078367277299340503872124124714036499367887886486264658590613431293656417255355575602576047502506125375605713228912611320198066713358654181533335650785578352716562937038768171269136647529849805172492594142026261051266577821582011917001752590659862613307646536049830151262848916867223615064832279222
c= 375617816311787295279632219241669262704366237192565344884527300748210925539528834207344757670998995567820735715933908541800125317082581328287816628816752542104514363629022246620070560324071543077301256917337165566677142545053272381990573611757629429857842709092285442319141751484248315990593292618113678910350875156232952525787082482638460259354559904243062546518553607882194808191571131590524874275187750985821420412987586148770397073003186510357920710387377990379862185266175190503647626248057084923516190642292152259727446111686043531725993433395002330208067534104745851308178560234372373476331387737629284961288204368572750848248186692623500372605736825205759172773503283282321274793846281079650686871355211691681512637459986684769598186821524093789286661348936784712071312135814683041839882338235290487868969391040389837253093468883093296547473466050960563347060307256735803099039921213839491129726807647623542881247210251994139130146519265086673883077644185971830004165931626986486648581644383717994174627681147696341976767364316172091139507445131410662391699728189797082878876950386933926807186382619331901457205957462337191923354433435013338037399565519987793880572723211669459895193009710035003369626116024630678400746946356
n= 728002565949733279371529990942440022467681592757835980552797682116929657292509059813629423038094227544032071413317330087468458736175902373398210691802243764786251764982802000867437756347830992118278032311046807282193498960587170291978547754942295932606784354258945168927044376692224049202979158068158842475322825884209352566494900083765571037783472505580851500043517614314755340168507097558967372661966013776090657685241689631615245294004694287660685274079979318342939473469143729494106686592347327776078649315612768988028622890242005700892937828732613800620455225438339852445425046832904615827786856105112781009995862999853122308496903885748394541643702103368974605177097553007573113536089894913967154637055293769061726082740854619536748297829779639633209710676774371525146758917646731487495135734759201537358734170552231657257498090553682791418003138924472103077035355223367678622115314235119493397080290540006942708439607767313672671274857069053688258983103863067394473084183472609906612056828326916114024662795812611685559034285371151973580240723680736227737324052391721149957542711415812665358477474058103338801398214688403784213100455466705770532894531602252798634923125974783427678469124261634518543957766622712661056594132089
q = gmpy2.gcd((pow(c1,e2,n) * pow(5,e1*e2,n) - pow(c2,e1,n) * pow(2,e1*e2,n)),n)
p = n // q
assert p*q == n
print(p*q == n)
phi = (p-1)*(q-1)
e=65537
d = gmpy2.invert(e,phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#SYC{poly_rsa_Just_need5_s1mple_gcd}Simple3DES
题目信息
题目链接:nc 59.110.20.54:23333 https://blog.csdn.net/Mr_wzc/article/details/121713518
查看代码
from Crypto.Cipher import DES3
from Crypto.Util.number import *
import os
import random
import string
import hashlib
xor = lambda a,b: bytes([a[i % len(a)] ^ b[i % len(b)] for i in range(max(len(a), len(b)))])
pad = lambda msg,padlen: msg+chr((padlen-(len(msg)%padlen))).encode()*(padlen-(len(msg)%padlen))
flag = os.environ.get("FLAG", "SYC{Al3XEI_FAKE_FLAG}").encode()
sec = os.urandom(8)
banner = '|'*70
DEBUG = False
def proof_of_work():
if DEBUG:
return True
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
digest = hashlib.sha256(proof.encode()).hexdigest()
print("sha256(XXXX+%s) == %s" % (proof[4:], digest))
x = input("Give me XXXX: ")
if len(x)!=4 or hashlib.sha256((x+proof[4:]).encode()).hexdigest() != digest:
return False
print("Right!")
return True
def enc(msg,key):
try:
key = long_to_bytes(key)
msg = xor(long_to_bytes(msg),sec)
des = DES3.new(key,DES3.MODE_ECB)
ct = xor(des.encrypt(pad(msg,8)),sec)
return bytes_to_long(ct)
except Exception as e:
print(e)
return Exception
def service():
cnt = 0
if not proof_of_work():
exit()
print(banner)
print('Simple DES Encryption Service')
print(banner)
while cnt<2:
print('1. Encrypt\n2. Get encrypted flag.')
choice = int(input('> '))
if choice == 1:
print('Input msg:')
msg = int(input('> ').strip())
print('Input key:')
key = int(input('> ').strip())
print(enc(msg,key))
elif choice == 2:
print('Input key:')
key = int(input('> ').strip())
print(enc(bytes_to_long(flag),key))
else:
exit()
cnt+=1
print(banner)
print('Bye!')
exit()
try:
service()
except Exception:
print("Something goes wrong...\n")
print(banner+'\n')
exit()我的解答:
EXP:
from hashlib import sha256
import random
from pwn import *
import string
from Crypto.Util.number import *
dir = string.ascii_letters + string.digits
conn = remote("59.110.20.54", 23333)
conn.recvuntil(b'sha256(XXXX+')
salt = conn.recv(16).strip().decode()
conn.recvuntil(b') == ')
hash = conn.recv(64).strip().decode()
while True:
rand_str = (''.join([random.choice(dir) for _ in range(4)])) + salt
if sha256(rand_str.encode()).hexdigest() == hash:
print("",rand_str[:4])
conn.sendlineafter(b'Give me XXXX:', rand_str[:4])
break
#conn.interactive()
key1 = b"\x01\x01\x01\x01\x01\x01\x01\x01"
key2 = b"\xfe\xfe\xfe\xfe\xfe\xfe\xfe\xfe"
key = key1 + key2
conn.sendlineafter("> ", '2')
conn.sendlineafter("> ", str(bytes_to_long(key)))
ct = int(conn.recvline())
conn.sendlineafter("> ", '1')
conn.sendlineafter("> ", str(ct))
conn.sendlineafter("> ", str(bytes_to_long(key)))
flag = long_to_bytes(int(conn.recvline()))
print(flag)
#SYC{DES_1s_0ut_0f_t1me}赛后跟别的师傅交流了一些其他解法,这里也分享一下:
从pad入手,可以注意到enc中加密流程中有个漏洞:
进行3DES加密
出题人将msg与sec异或后,再进行填充。而填充的方式如下:
pad = lambda msg,padlen: msg+chr((padlen-(len(msg)%padlen))).encode()*(padlen-(len(msg)%padlen))
DES以8字节为一组进行分组加密。而这个pad是在msg恰好为8字节的整数倍时,仍然会进行8字节b"\x08"的填充。
也就是说,如果我们发送一个空的字节串,对应的数字也就是0,那么靶机端加密的流程应该是:
进行3DES加密
而由于8字节为一组加密,所以第二组的密文值应该是:
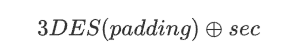
而我们已经有了密钥,自然也就能获得3DES(padding)的值了,和密文进行异或就能得到sec的值。
有了sec之后,输入2申请flag的密文,后面就好办了。
exp:
from Crypto.Util.number import *
from Crypto.Cipher import DES3
from pwn import *
from tqdm import *
from hashlib import sha256
#context.log_level = 'debug'
def proof_of_work():
table = string.digits + string.ascii_letters
temp = r.recvuntil(b"sha256(XXXX+")
temp = r.recvline()
suffix = temp[:16].decode()
hex1 = temp[20:].strip().decode()
for i in tqdm(table):
for j in table:
for k in table:
for m in table:
temp1 = i+j+k+m
if(sha256((temp1+suffix).encode()).hexdigest() == hex1):
r.sendline(temp1.encode())
return
r = remote("59.110.20.54", 23333)
proof_of_work()
xor = lambda a,b: bytes([a[i % len(a)] ^ b[i % len(b)] for i in range(max(len(a), len(b)))])
#2
r.recvuntil(b"Get encrypted flag.")
r.recvuntil(b"> ")
r.sendline(b"2")
r.recvuntil(b"> ")
key = b"1234567887654321"
des = DES3.new(key,DES3.MODE_ECB)
r.sendline(str(bytes_to_long(key)).encode())
enc = long_to_bytes(int(r.recvline().strip().decode()))
#1
r.recvuntil(b"Get encrypted flag.")
r.recvuntil(b"> ")
r.sendline(b"1")
r.recvuntil(b"> ")
r.sendline(b"0")
r.recvuntil(b"> ")
r.sendline(str(bytes_to_long(key)).encode())
enc1 = long_to_bytes(int(r.recvline().strip().decode()))
#dec
padding = b"\x08"*8
enc_pad1 = des.encrypt(padding)
sec = xor(enc_pad1,enc1)[-8:]
temp = xor(des.decrypt(xor(sec,enc)),sec)
print(temp)[+] Opening connection to 59.110.20.54 on port 23333: Done
42%|█████████████████████████████████████████
b'SYC{DES_1s_0ut_0f_t1me}M'JPGDiff
图片中的字符串即为flag


我的解答:
因为图片长度是1*65536,因此解密出的图片长宽是256x256
Hint:给了我们一张图

之前第五届强网杯出过类似题,希伯尔特矩阵
以16*16的希伯尔特举例,以箭头方向排列图片像素,可以得到结果
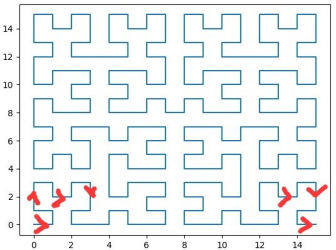
所以第一步先将附件图片转换rgb数值
脚本:
from PIL import Image
def got_RGB(img_path):
img = Image.open(img_path)
width, height = img.size
img = img.convert('RGB')
array = []
for i in range(width):
for j in range(height):
r, g, b = img.getpixel((i, j))
if r != 0:
print( r,g,b)
rgb = (r, g, b)
array.append(rgb)
if __name__ == "__main__":
img_path = r"ct.png" # 图像路径
got_RGB(img_path)输出结果:
处理一下数据带上[]保存到output (1).txt
希伯尔特脚本:
import numpy
from PIL import Image
import matplotlib.pyplot as plt
def _hilbert(direction, rotation, order):
if order == 0:
return
direction += rotation
_hilbert(direction, -rotation, order - 1)
step1(direction)
direction -= rotation
_hilbert(direction, rotation, order - 1)
step1(direction)
_hilbert(direction, rotation, order - 1)
direction -= rotation
step1(direction)
_hilbert(direction, -rotation, order - 1)
def step1(direction):
next = {0: (1, 0), 1: (0, 1), 2: (-1, 0), 3: (0, -1)}[direction & 0x3]#取后两位?
global x, y
x.append(x[-1] + next[0])
y.append(y[-1] + next[1])
def hilbert(order):
global x, y
x = [0,]
y = [0,]
_hilbert(0, 1, order)
return (x, y)
def main1():
x, y = hilbert(8)
plt.plot(x, y)
plt.show()
print(x,y)
if __name__ == "__main__":
main1()
x1 = x[::-1]
y1 = y[::-1]
r0 = []
g0 = []
b0 = []
f = open('output (1).txt')
a = f.read()
f.close()
a1 = a.split('\n')
for i in range(0,256):
r0.append([])
g0.append([])
b0.append([])
for j in range(0,256):
r0[-1].append(0)
g0[-1].append(0)
b0[-1].append(0)
for i in a1:
print(i)
cur = i.split('[')[1].split(']')[0]
cur1 = cur.split(' ')
cur2 = []
for i in cur1:
try:
cur2.append(int(i))
except:
pass
x_p = x.pop()
y_p = y.pop()
r0[x_p][y_p]=cur2[0]
g0[x_p][y_p]=cur2[1]
b0[x_p][y_p]=cur2[2]
print(len(r0))
print(len(r0[0]))
print(r0[0][0])
print(g0[0][0])
print(b0[0][0])
r1 = numpy.asarray(r0)
g1 = numpy.asarray(g0)
b1 = numpy.asarray(b0)
r = Image.fromarray(r1).convert('L')
g = Image.fromarray(g1).convert('L')
b = Image.fromarray(b1).convert('L')
image = Image.merge('RGB',(r,g,b))
image.save('out1.jpg')代码解析:
- 通过Hilbert曲线生成一系列的坐标点,并用于图像的像素位置。Hilbert曲线是一个无限长的分形曲线,通常用于生成复杂的图案。
- 从名为"output(1).txt"的文件中读取数据,并按照Hilbert曲线的坐标位置,将文件中的数据分别赋值给红、绿、蓝三种颜色通道。
- 使用matplotlib库将Hilbert曲线绘制出来。
- 使用PIL库将读取的数据文件转换为图像,并保存为"out1.jpg"。
运行得到flag:

Energetic_Carcano
题目链接:nc 59.110.20.54:8763 https://en.wikipedia.org/wiki/Elliptic-curve_cryptography
查看代码
# from sage.all import *
import os
import random
import string
import hashlib
from Crypto.Util.number import *
DEBUG = True
banner = '|'*70
flag = os.environ.get("FLAG", b"SYC{Al3XEI_FAKE_FLAG}").encode()
pbits = 120
abp = "abp"
def proof_of_work():
if DEBUG:
return True
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
digest = hashlib.sha256(proof.encode()).hexdigest()
print("sha256(XXXX+%s) == %s" % (proof[4:], digest))
x = input("Give me XXXX: ")
if len(x)!=4 or hashlib.sha256((x+proof[4:]).encode()).hexdigest() != digest:
return False
print("Right!")
return True
def check(a,b,p,turn,ans):
if DEBUG:
return True
try:
if turn == "a":
return int(a) == ans
if turn == "b":
return int(b) == ans
if turn == "p":
return int(p) == ans
except Exception:
exit()
try:
if not proof_of_work():
exit()
print(banner)
print('\nHi Crypto-ers! AL3XEI here. I know you are excellent at math, so I prepared a game for u.')
print('In the equation y^2 = x^3+ a*x + b (mod p), 4 points are given. Plz give me the right a, b or p to contine the game.')
print('Good Luck!\n')
print(banner+'\n')
for i in range(10):
turn = random.choice(abp)
p = getPrime(pbits)
a,b = [next_prime(random.randint(2,p)) for _ in "ab"]
curve = EllipticCurve(GF(p),[a,b])
pts = [curve.random_point() for _ in range(4)]
pts = [(_[0], _[1]) for _ in pts]
for _ in pts:
print(_,end=" ")
print('\nGive me '+turn+" :")
ans = int(input('> '))
if check(a,b,p,turn,ans):
print("Good! Next challenge->\n")
print(banner+'\n')
pbits+=5
continue
else:
print("Something goes wrong...\n")
print(banner+'\n')
exit()
print('Congrats! Your flag is:',flag)
except Exception:
print("Something goes wrong...\n")
print(banner+'\n')
exit() 我的解答:
首先对sha256加密的内容进行爆破
import hashlib
dic = 'abcdefghijklmnopqrstuvwxyz1234567890ABCDEFGHIJKLMNOPQRSTUVWXYZ'
for a in dic:
for b in dic:
for c in dic:
for d in dic:
t =str(a)+str(b)+str(c)+str(d)+'Nlw6brvPdZGVIq69'
m = (hashlib.sha256(t.encode())).hexdigest()
if m[:64] == '6415c15da02b00c065b64adb488c5637254e11a71a870bd5233bb1188a26e853':
print(t)
break
#yH60Nlw6brvPdZGVIq69输入靶机得到
sha256(XXXX+Nlw6brvPdZGVIq69) == 6415c15da02b00c065b64adb488c5637254e11a71a870bd5233bb1188a26e853
Give me XXXX: yH60
Right!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hi Crypto-ers! AL3XEI here. I know you are excellent at math, so I prepared a game for u.
In the equation y^2 = x^3+ a*x + b (mod p), 4 points are given. Plz give me the right a, b or p to contine the game.
Good Luck!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(378051270493977219649402828259979752, 130518506787701045136993765726508477) (749006871592536724029074691688477196, 546465207758611318117126300707802113) (418056702786701446653913509899377929, 514811686361648235081218463920442308) (409605229366679928143097344219915774, 280863993190286248114375496984538036)
Give me a :
> 之后给我们椭圆曲线的四个点,要我们求出a,b,p
并按照要求给题目需要的值:
str_data ="(378051270493977219649402828259979752, 130518506787701045136993765726508477) (749006871592536724029074691688477196, 546465207758611318117126300707802113) (418056702786701446653913509899377929, 514811686361648235081218463920442308) (409605229366679928143097344219915774, 280863993190286248114375496984538036)"
numbers = str_data.split(" (")
C1 = [int(x) for x in numbers[0].replace("(", "").replace(")", "").split(",")]
# 将第一个括号中的数值转为整数列表
C2 = [int(x) for x in numbers[1].replace("(", "").replace(")", "").split(",")]
# 将第二个括号中的数值转为整数列表
C3 = [int(x) for x in numbers[2].replace("(", "").replace(")", "").split(",")]
# 将第三个括号中的数值转为整数列表
C4 = [int(x) for x in numbers[3].replace("(", "").replace(")", "").split(",")]
# 将第四个括号中的数值转为整数列表上述代码把题目给的字符串变成四个点
t1,s1=C1[0],C1[1]**2-C1[0]**3
t2,s2=C2[0],C2[1]**2-C2[0]**3
t3,s3=C3[0],C3[1]**2-C3[0]**3
t4,s4=C4[0],C4[1]**2-C4[0]**3
kn1=(t1-t2)*(s1-s3)-(t1-t3)*(s1-s2)
kn2=(t2-t3)*(s2-s4)-(t2-t4)*(s2-s3)
n=gcd(kn1,kn2)利用上述代码求出椭圆曲线模数的倍数,之后求他们的公约数
因为公约数得到的有时不一定是素数,所以我们还需要对其进行分解得到正确的椭圆曲线模数
之后据此求出a,b
while True:
if n%2==0:
n=n//2
else:
break
for i in range(1,999999):
if n%i==0:
n=n//i
if isPrime(n):
break
print(isPrime(n))
a=(s1-s2)*inverse(t1-t2,n)%n
b=(s1-t1*a)%n
print(a)
print(b)
print(n)完整exp:
from tqdm import tqdm
from Crypto.Util.number import inverse, isPrime
from gmpy2 import gcd
str_data ="(378051270493977219649402828259979752, 130518506787701045136993765726508477) (749006871592536724029074691688477196, 546465207758611318117126300707802113) (418056702786701446653913509899377929, 514811686361648235081218463920442308) (409605229366679928143097344219915774, 280863993190286248114375496984538036)"
numbers = str_data.split(" (")
C1 = [int(x) for x in numbers[0].replace("(", "").replace(")", "").split(",")]
# 将第一个括号中的数值转为整数列表
C2 = [int(x) for x in numbers[1].replace("(", "").replace(")", "").split(",")]
# 将第二个括号中的数值转为整数列表
C3 = [int(x) for x in numbers[2].replace("(", "").replace(")", "").split(",")]
# 将第三个括号中的数值转为整数列表
C4 = [int(x) for x in numbers[3].replace("(", "").replace(")", "").split(",")]
# 将第四个括号中的数值转为整数列表
t1,s1=C1[0],C1[1]**2-C1[0]**3
t2,s2=C2[0],C2[1]**2-C2[0]**3
t3,s3=C3[0],C3[1]**2-C3[0]**3
t4,s4=C4[0],C4[1]**2-C4[0]**3
kn1=(t1-t2)*(s1-s3)-(t1-t3)*(s1-s2)
kn2=(t2-t3)*(s2-s4)-(t2-t4)*(s2-s3)
n=gcd(kn1,kn2)
while True:
if n%2==0:
n=n//2
else:
break
for i in range(1,999999):
if n%i==0:
n=n//i
if isPrime(n):
break
print(isPrime(n))
a=(s1-s2)*inverse(t1-t2,n)%n
b=(s1-t1*a)%n
print(a)
print(b)
print(n)
#True
29277359338914510540136062193641803
232628153989170416007866897639439937
774389452478762633230646952132560131整体打靶情况如下:
查看代码
(378051270493977219649402828259979752, 130518506787701045136993765726508477) (749006871592536724029074691688477196, 546465207758611318117126300707802113) (418056702786701446653913509899377929, 514811686361648235081218463920442308) (409605229366679928143097344219915774, 280863993190286248114375496984538036)
Give me a :
> 29277359338914510540136062193641803
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(23078430191430551911422770371482241525, 4747368848920480112568596025362678862) (8617860111903913207396034585801998741, 8515336546833565502105963912820215479) (4868013779269837310771183248749142881, 17590472117045597992767230650401502944) (10680111076720326821200958023334554954, 10775315966100347404114559980258600144)
Give me a :
> 17929406418359922216265239477958827797
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10771122288335239133266005310830531012, 389508216199223724926400997369474147024) (230158601919313903953356203566330438517, 444382509174609849851216345269926492915) (191128296573799814148625017670638739422, 860896249648448806722257672353546514506) (709699332966383447079056236787511584760, 946072760213053615791525317007415753546)
Give me b :
> 85069270132352375381740275323507634031
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(16093415706079510505564267489532638382687, 15823631826808919673415954635558942618101) (9327527293338571074085244032629951670583, 21302089564007778275418312492662836679299) (20889143820526267787143498723922805645551, 5624675018314310666041404773691472999083) (21510938227834564677066871838809084175326, 20956807592542408282128121169678568856658)
Give me b :
> 16622549821568431487848337441400801341227
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(10217173028311971144706800628455761423291, 430790004422987657145058355735096442602889) (141752894842643866465562858995750012726384, 58980478860896262185917461398800904806986) (456756194566162486005306102405931323273360, 530134910802771885301776935623897600701520) (907425622685188543917631798509077597409359, 59726033761647937174923431098131126279646)
Give me a :
> 829975307230762835609740726685601153870227
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(9667185205107839188032287391833520005354453, 19501232459926284581712835877109211640425858) (27104941655631938220714462901761499261043715, 6554023943285720628478110880423534307104146) (16352724251125925571390551316952168465102162, 21724840027565599825190757161211756106910412) (10771277136207250520813859293698103879029316, 18322770968786245706378741920683251532311789)
Give me a :
> 21342952699955082143134173278135630380397101
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(841737630918946442223369605148724647648249889, 401200627561387480954923429604498081329501263) (654069758499797765068267130606853506446450005, 464130365497791721329120199743778241014340980) (190150666108315634628838183058499959686694195, 327770687272325392132109691807378994619602184) (43851049667156947099465894154568478890166335, 478903557554066160405390159052218528704738184)
Give me b :
> 851288263220161437169240279325141204085487619
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(21109319300007682592941602611214650653872454062, 5497846351948893634260792598419846257947609282) (21493031472267383692517458274592622453212748691, 15556037884592198896769676162545860047550256455) (22958013371606100300171106415623928694769705176, 1874906364603748150568674333073697060433815363) (17973629598703080743041508141178048237602138070, 3637949709132881319018254957474457874815133776)
Give me p :
> 24338416484546066034541134360821544565205755411
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(501284201101950008486821064612213936153066900730, 348425719491505801108201500130656288467958209738) (649473801528997228493160512099604056678067531305, 770941733154873970760287156564416585110176824469) (442219410474433253284616485308346706211577911949, 113428936149673031263995188619389859490396583171) (465339862407726409036504623273289960953333529332, 328005466697862026646742897400738357557211732268)
Give me b :
> 139267982907934728205781418136266513913760448833
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(36482071903895732006432750342148505107923662114570, 4729553879352066788468408751621320687883717975456) (12297887079875810591227530841884613090011286959721, 29883518693408668664136928156105360941696603414415) (9462024954085612543231007596113266366913551591075, 3765848537068598832568812513353106151807257471538) (26948640414302527580423202633668379136488389491269, 38371014060798358533370822520947822810987073802604)
Give me b :
> 34151346456620556554682930555174038517164712559813
Good! Next challenge->
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Congrats! Your flag is: b'SYC{ECC_M4ster}'这里也分享一下偶像的解法:
题意很简单,完成十轮挑战就能获得flag,每轮挑战内容为:
我们知道椭圆曲线的点满足方程:
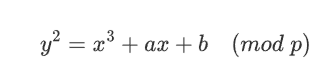
而我们有四个点的坐标,因此就有四组方程:
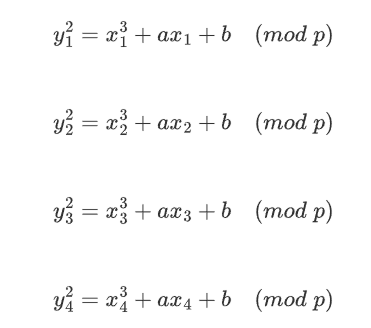
要求从四组方程中还原a、b、p,其实跟无参数的LCG很像,主要目的就是消元,求gcd得到p,然后再回到模方程中求解a、b。
消元过程如下,我们取前两组方程:
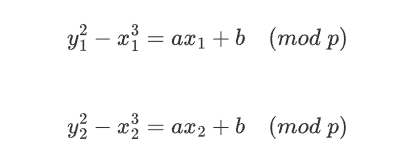
做差消掉b:
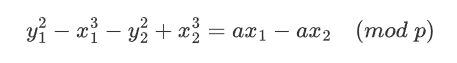
把a单独提出来:
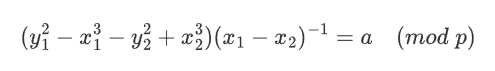
同理,我们取第二三组方程也能得到:
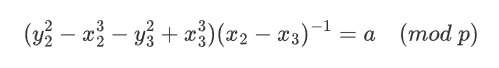
做差得到:
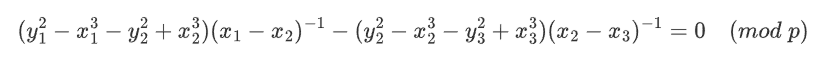
那么同样再取一组求gcd,并消去小因子就能得到p,得到p过后还原ab就很轻松。
exp:
from Crypto.Util.number import *
from pwn import *
from tqdm import *
from hashlib import sha256
#context.log_level = 'debug'
def proof_of_work():
table = string.digits + string.ascii_letters
temp = r.recvuntil(b"sha256(XXXX+")
temp = r.recvline()
suffix = temp[:16].decode()
hex1 = temp[20:].strip().decode()
for i in tqdm(table):
for j in table:
for k in table:
for m in table:
temp1 = i+j+k+m
if(sha256((temp1+suffix).encode()).hexdigest() == hex1):
r.sendline(temp1.encode())
return
def calc(points):
(x1,y1),(x2,y2),(x3,y3),(x4,y4) = points
t1 = (y2**2-y1**2-x2**3+x1**3)
t2 = (y3**2-y2**2-x3**3+x2**3)
t3 = (y4**2-y3**2-x4**3+x3**3)
k1p = t1*(x3-x2) - t2*(x2-x1)
k2p = t2*(x4-x3) - t3*(x3-x2)
k3p = t1*(x4-x3) - t3*(x2-x1)
p = GCD(k1p,k2p)
p = GCD(p,k3p)
for i in range(2,1000):
while(p % i == 0):
p //= i
a = inverse(x2-x1,p)*t1 % p
b = (y1**2-x1**3-a*x1) % p
return a,b,p
r = remote("59.110.20.54",8763)
proof_of_work()
r.recvuntil(b"Good Luck!")
for i in range(10):
r.recvuntil(b"|"*70)
r.recvline()
r.recvline()
points = r.recvline().strip().decode().split(" ")
point_list = [[0,0] for k in range(4)]
for j in range(8):
if(j % 2 == 0):
point_list[j//2][0] = int(points[j][1:-1])
else:
point_list[j//2][1] = int(points[j][:-1])
a,b,p = calc(point_list)
r.recvuntil(b"me ")
turn = r.recvline()
if(b"a" in turn):
r.sendline(str(a).encode())
if(b"b" in turn):
r.sendline(str(b).encode())
if(b"p" in turn):
r.sendline(str(p).encode())
r.recvuntil(b"Congrats! Your flag is:")
print(r.recvline()) 
Just need One
题目链接:nc 59.110.20.54:2613 One bullet to kill all Outlaws.
查看代码
import os
import random
import string
import hashlib
flag = os.environ.get("FLAG", b"SYC{Al3XEI_FAKE_FLAG}")
DEBUG = False
banner = '|'*70
if DEBUG:
print("==DEBUG MODE==")
def proof_of_work():
if DEBUG:
return True
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
digest = hashlib.sha256(proof.encode()).hexdigest()
print("sha256(XXXX+%s) == %s" % (proof[4:], digest))
x = input("Give me XXXX: ")
if len(x)!=4 or hashlib.sha256((x+proof[4:]).encode()).hexdigest() != digest:
return False
print("Right!")
return True
try:
if not proof_of_work():
exit()
print(banner)
parms = [random.getrandbits(32) for _ in range(128)]
res = res = int(input('Give me x calculating f(x) :\n> '))
if res >= 2**32:
print("Give me something smaller.\n")
print(banner+'\n')
exit()
cnt = 0
for _ in range(128):
cnt += pow(res,_)*parms[_]
print(cnt)
ans = input('Give me Coefficients :\n> ')
ans = [int(_) for _ in ans.split(",")]
if ans == parms:
print('Congrats! Your flag is:',flag)
else:
exit()
except Exception:
print("Something goes wrong...\n")
print(banner+'\n')
exit() 我的解答:
连接靶机
sha256(XXXX+FeTrNNv0gxOL9Avg) == 2ed39ee537e75012be16a79206b0666fce0fb62d9834c4a510b1cc8d0bd40092
Give me XXXX: u7dt
Right!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Give me x calculating f(x) :
> 已知 cnt = base^0^ * p1 + base^1^ * p2 + base^2^ * p3 + ... + base^127^ * p128
可以考虑通过取模来得到p1-p128
这里取base = prevprime(2**32)
因为p是32位整数 取小了会丢失信息 取大过不了检测
然后进行分解
sha256(XXXX+FeTrNNv0gxOL9Avg) == 2ed39ee537e75012be16a79206b0666fce0fb62d9834c4a510b1cc8d0bd40092
Give me XXXX: u7dt
Right!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Give me x calculating f(x) :
> 4294967291
489057694294647008538200027295937157126142904476422163217167869312544926391154656551482308741762631738430298400781587956802144416760947708882643687396077108406962882557467283971280484703510744634949508976007526764554042691324293221504014468155015953394470600296752077238905241072132593560519581135041295710191182824057039630800074288554132502716717374034070277374144612818741105884811462468422358822988880033011705924156915408984793688420709296168344478980614912552654204520050424147127660733204596123539563217230772755473091707250859354020603000251323856606463073456341400443416224434074441190878505611871873651313236682769677581250335030316135184123469521525394775215704614264167696724669615005917840560015939905448985586215560601988359643704102180159336602542217772666144664818991611674822987956885864823443441958962152096587341346023146378665711260756814726241412333341045119972992768411141174969226198822291690350839893034132755654998681666294127812318232032092566027263166201113871772661654076617164772799209797354130820480529528599309135852457751583312030638274715844266639671878061309074488935690049119103399461554412016571335863934632753521401800986472748950867438911373101696350408017218169517236223495373928940610251950682
Give me Coefficients :
> from sympy import prevprime
c = 489057694294647008538200027295937157126142904476422163217167869312544926391154656551482308741762631738430298400781587956802144416760947708882643687396077108406962882557467283971280484703510744634949508976007526764554042691324293221504014468155015953394470600296752077238905241072132593560519581135041295710191182824057039630800074288554132502716717374034070277374144612818741105884811462468422358822988880033011705924156915408984793688420709296168344478980614912552654204520050424147127660733204596123539563217230772755473091707250859354020603000251323856606463073456341400443416224434074441190878505611871873651313236682769677581250335030316135184123469521525394775215704614264167696724669615005917840560015939905448985586215560601988359643704102180159336602542217772666144664818991611674822987956885864823443441958962152096587341346023146378665711260756814726241412333341045119972992768411141174969226198822291690350839893034132755654998681666294127812318232032092566027263166201113871772661654076617164772799209797354130820480529528599309135852457751583312030638274715844266639671878061309074488935690049119103399461554412016571335863934632753521401800986472748950867438911373101696350408017218169517236223495373928940610251950682
base = prevprime(2**32)
tem = [c % base**(i+1) for i in range(128)]
tem2 = [tem[0]]+[tem[i+1] - tem[i] for i in range(127)]
res = [tem2[0]]+[tem2[i] // (base**i) for i in range(1,128)]
rr = (str(res).replace(" ", "").replace("[", "").replace("]", ""))
cnt = 0
for _ in range(128):
cnt += pow(base, _)*res[_]
assert(cnt == c)
print(rr)
#3523332454,3806256003,1275741753,217046321,3106457397,1635652588,2226935506,3347445675,2427364460,1805694802,2173955074,923550160,3288310170,1876921246,515401300,3407844517,2224882041,3116295164,3219358567,1342418093,576569956,3183456771,2589341238,1513108906,814904475,1806127418,821988618,2112102471,2323218383,2034630806,1569848760,3999100044,1694618776,1684570114,509662222,1097691320,2287872167,259149930,309735559,2056621141,2879107592,2507924071,4222845248,215081135,4247489058,1085229413,409624918,641738323,2638374117,1818228668,3018707086,251669285,3621557421,4083883739,1148020081,3374929590,1488008314,1311838905,1097738122,4188622406,3377579298,747928469,3691984274,2610282950,2051685464,332178494,3725105622,3682233714,1827447525,3003505025,1435907700,2538932246,3331642462,1580962879,60301064,1454490335,3668382407,3762573493,3749845060,4183626863,3198701880,9415399,2318959134,2642110800,2754780783,87190321,2975771559,777990136,933241507,3098302527,4284187333,464737477,2177225887,760796154,3646746796,323704849,3016511558,2749093615,2924814121,3696370037,592837845,891108574,62451208,3395128166,652649904,3382875261,1030690805,1083043260,1892699021,2407213858,2077889134,2392101266,2308776565,1358691887,2197318773,1084010548,1086165563,280758500,380698017,2199079607,871830897,1988087443,2194784616,415388342,2952660519,120801411,3378855991,2011211676> 3523332454,3806256003,1275741753,217046321,3106457397,1635652588,2226935506,3347445675,2427364460,1805694802,2173955074,923550160,3288310170,1876921246,515401300,3407844517,2224882041,3116295164,3219358567,1342418093,576569956,3183456771,2589341238,1513108906,814904475,1806127418,821988618,2112102471,2323218383,2034630806,1569848760,3999100044,1694618776,1684570114,509662222,1097691320,2287872167,259149930,309735559,2056621141,2879107592,2507924071,4222845248,215081135,4247489058,1085229413,409624918,641738323,2638374117,1818228668,3018707086,251669285,3621557421,4083883739,1148020081,3374929590,1488008314,1311838905,1097738122,4188622406,3377579298,747928469,3691984274,2610282950,2051685464,332178494,3725105622,3682233714,1827447525,3003505025,1435907700,2538932246,3331642462,1580962879,60301064,1454490335,3668382407,3762573493,3749845060,4183626863,3198701880,9415399,2318959134,2642110800,2754780783,87190321,2975771559,777990136,933241507,3098302527,4284187333,464737477,2177225887,760796154,3646746796,323704849,3016511558,2749093615,2924814121,3696370037,592837845,891108574,62451208,3395128166,652649904,3382875261,1030690805,1083043260,1892699021,2407213858,2077889134,2392101266,2308776565,1358691887,2197318773,1084010548,1086165563,280758500,380698017,2199079607,871830897,1988087443,2194784616,415388342,2952660519,120801411,3378855991,2011211676
Congrats! Your flag is: SYC{Alg0r1thm_1s_s0_S1mpl3!}来看看偶像的解法:
这道题的题意如下:
生成长度为128的序列,序列中每个值是随机的32比特
解决方式也很简单,注意到它其实只限制了res小于2^32,那么我们传入负数的话,绝对值大小是不会检查的。
所以直接传-2^32或更小的2的幂次,然后将累加和逐次移位并处理对应的减法借位就有parms了。
exp:
from Crypto.Util.number import *
from pwn import *
from tqdm import *
from hashlib import sha256
#context.log_level = 'debug'
def proof_of_work():
table = string.digits + string.ascii_letters
temp = r.recvuntil(b"sha256(XXXX+")
temp = r.recvline()
suffix = temp[:16].decode()
hex1 = temp[20:].strip().decode()
for i in tqdm(table):
for j in table:
for k in table:
for m in table:
temp1 = i+j+k+m
if(sha256((temp1+suffix).encode()).hexdigest() == hex1):
r.sendline(temp1.encode())
return
r = remote("59.110.20.54", 2613)
proof_of_work()
r.recvuntil(b"> ")
res = -2**64
r.sendline(str(res).encode())
cnt = int(r.recvline().strip().decode())
tt = cnt
r.recvuntil(b"> ")
parms = [0 for i in range(128)]
for i in range(128):
parms[i] = cnt & ((1<<64)-1)
if(i%2):
parms[i] = 2**64-parms[i]
elif(i!=0 and i%2 == 0):
parms[i] += 1
cnt >>= 64
r.sendline(str(parms)[1:-1].encode())
print(r.recvline())
Fi1nd_th3_x'
听说在那个大陆有位叫jrl777的旅行者......Cryptoer穿越到了提瓦特就要拿出真本事!
CRsaT.py
查看代码
from Crypto.Util.number import *
from libnum import*
from secret import flag
p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
e = getPrime(32)
n = p*q*r
phi = (p-1)*(q-1)*(r-1)
d = inverse(e,phi)
dP = d%((q-1)*(r-1))
dQ = d%((p-1)*(r-1))
dR = d%((p-1)*(q-1))
m = s2n(flag.encode())
c = pow(m,e,n)
print('p=',p)
print('q=',q)
print('r=',r)
print('dP=',dP)
print('dQ=',dQ)
print('dR=',dR)
print('c=',c)
'''
p= 13014610351521460822156239705430709078128228907778181478242620569429327799535062679140131416771915929573454741755415612880788196172134695027201422226050343
q= 12772373441651008681294250861077909144300908972709561019514945881228862913558543752401850710742410181542277593157992764354184262443612041344749961361188667
r= 12128188838358065666687296689425460086282352520167544115899775800918383085863282204525519245937988837403739683061218279585168168892037039644924073220678419
dP= 116715737414908163105708802733763596338775040866822719131764691930369001776551671725363881836568414327815420649861207859100479999650414099346914809923964116101517432576562641857767638396325944526867458624878906968552835814078216316470330511385701105459053294771612727181278955929391807414985165924450505855941
dQ= 44209639124029393930247375993629669338749966042856653556428540234515804939791650065905841618344611216577807325504984178760405516121845853248373571704473449826683120387747977520655432396578361308033763778324817416507993263234206797363191089863381905902638111246229641698709383653501799974217118168526572365797
dR= 60735172709413093730902464873458655487237612458970735840670987186877666190533417038325630420791294593669609785154204677845781980482700493870590706892523016041087206844082222225206703139282240453277802870868459288354322845410191061009582969848870045522383447751431300627611762289800656277924903605593069856921
c= 93063188325241977486352111369210103514669725591157371105152980481620575818945846725056329712195176948376321676112726029400835578531311113991944495646259750817465291340479809938094295621728828133981781064352306623727112813796314947081857025012662546178066873083689559924412320123824601550896063037191589471066773464829226873338699012924080583389032903142107586722373131642720522453842444615499672193051587154108368643495983197891525747653618742702589711752256009
'''Task.txt
5Lq65Lus5Y+q6K6w5b6X77yM6L+Z5pys5piv6aOO5ZKM5pel5Li955qE5LiA5aSp77yManJsNzc35q2j5Zyo572R5LiK5a2m5Lmg5a+G56CB5a2m44CC5b+954S25LmL6Ze077yM6buR6Imy5raI6YCA77yM5bGP5bmV55m95YWJ6aqk6LW377yM5omA5pyJ55qE6K665paH6YO95reh5Ye655y85biY44CC5LuW5Yed56We5LiA55yL77yM5Y205Y+q5pyJ5rex6YKD5aaC5aKo55qE4oCc5Y6f56We4oCd5LqM5a2X5Zyo5Zue5bqU552A44CC5pyq5Y+K5oCd6ICD77yManJsNzc36ISR6KKL5LiA6Zi15pmV55yp44CC6ICM5q2k5Yi777yM5o+Q55Om54m55aSn6ZmG5LiK56m65pyJ6YeR5YWJ6Zeq54OB77yM56m66Ze05Lmx5rWB5LmL5YaF77yM5LiD56eN5YWD57Sg5Yqb5pKV5byA5LqG5pe256m66KOC57yd77yM6aOO5bim5p2l5LqG5pWF5LqL55qE56eN5a2Q44CC5Y+v5YaN5Z2a5Zu655qE5bKp55+z5Lmf6Zq+6YCD56Oo5o2f55qE5ZG96L+Q44CC4oCc5LiW55WM77yM6YGX5b+Y5oiR44CC4oCd5LuW57uI56m25b+Y6K6w5LqG6Ieq5bexQ3J5cHRvZXLnmoTouqvku73jgILigJzmj5Dnk6bnibnlpKfpmYbnmoTml4XkurrvvIzkvaDog73mib7liLDmiJHpgZflpLHnmoTotKblj7flkJfvvJ/igJ0=我的解答:
附件给了Task.txt文件和py,txt用base64解码得到:
人们只记得,这本是风和日丽的一天,jrl777正在网上学习密码学。忽然之间,黑色消退,屏幕白光骤起,所有的论文都淡出眼帘。他凝神一看,却只有深邃如墨的“原神”二字在回应着。未及思考,jrl777脑袋一阵晕眩。而此刻,提瓦特大陆上空有金光闪烁,空间乱流之内,七种元素力撕开了时空裂缝,风带来了故事的种子。可再坚固的岩石也难逃磨损的命运。“世界,遗忘我。”他终究忘记了自己Cryptoer的身份。“提瓦特大陆的旅人,你能找到我遗失的账号吗?”
这个可以说是背景,主要还是看py文件,可知是中国剩余定理扩展求d。
exp:
from Crypto.Util.number import *
from sympy.ntheory.modular import crt
import gmpy2
p= 13014610351521460822156239705430709078128228907778181478242620569429327799535062679140131416771915929573454741755415612880788196172134695027201422226050343
q= 12772373441651008681294250861077909144300908972709561019514945881228862913558543752401850710742410181542277593157992764354184262443612041344749961361188667
r= 12128188838358065666687296689425460086282352520167544115899775800918383085863282204525519245937988837403739683061218279585168168892037039644924073220678419
dp= 116715737414908163105708802733763596338775040866822719131764691930369001776551671725363881836568414327815420649861207859100479999650414099346914809923964116101517432576562641857767638396325944526867458624878906968552835814078216316470330511385701105459053294771612727181278955929391807414985165924450505855941
dq= 44209639124029393930247375993629669338749966042856653556428540234515804939791650065905841618344611216577807325504984178760405516121845853248373571704473449826683120387747977520655432396578361308033763778324817416507993263234206797363191089863381905902638111246229641698709383653501799974217118168526572365797
dr= 60735172709413093730902464873458655487237612458970735840670987186877666190533417038325630420791294593669609785154204677845781980482700493870590706892523016041087206844082222225206703139282240453277802870868459288354322845410191061009582969848870045522383447751431300627611762289800656277924903605593069856921
c= 93063188325241977486352111369210103514669725591157371105152980481620575818945846725056329712195176948376321676112726029400835578531311113991944495646259750817465291340479809938094295621728828133981781064352306623727112813796314947081857025012662546178066873083689559924412320123824601550896063037191589471066773464829226873338699012924080583389032903142107586722373131642720522453842444615499672193051587154108368643495983197891525747653618742702589711752256009
b1 = (q-1)*(r-1)
b2 = (p-1)*(r-1)
b3 = (p-1)*(q-1)
d = crt([b1,b2,b3],[dp,dq,dr]) #crt([模],[余数])
for i in range(len(d)):
m = pow(c,d[i],p*q*r)
print(long_to_bytes(m))
#SYC{CRT_1s_f3n_but_Gen3hi_im9act_is_a_balabalaba}第三波题目
Quick_Robert
题目链接:nc 59.110.20.54:3042 https://en.wikipedia.org/wiki/Quadratic_residue
我的解答:
题目没有附件,我们连接靶机,一样是先过sha256
import hashlib
dic = 'abcdefghijklmnopqrstuvwxyz1234567890ABCDEFGHIJKLMNOPQRSTUVWXYZ'
for a in dic:
for b in dic:
for c in dic:
for d in dic:
t =str(a)+str(b)+str(c)+str(d)+'QW95ZPgXVuRorfn4'
m = (hashlib.sha256(t.encode())).hexdigest()
if m[:64] == 'a370900364689122fe95f332e5eb94cdc0ca9bfe94b072509adcf9f2b8306807':
print(t)
break
#YjaNQW95ZPgXVuRorfn4得到:
sha256(XXXX+QW95ZPgXVuRorfn4) == a370900364689122fe95f332e5eb94cdc0ca9bfe94b072509adcf9f2b8306807
Give me XXXX: YjaN
Right!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hi Crypto-ers! AL3XEI Here. In number theory, if there exists an integer q satisfying x^2=q(mod n), q is so called a quadratic residue.
We write this calculation as L(a,p), which its value shows a is or is not quadratic residue modulo p.
if p|a, L(a,p)=0; if a is a quadratic residue modulo p, L(a,p)=1; if a is not, L(a,p)=-1.
Below, you need to give me the answer of the sum of L(a*l**2+b*l+1,p), where a,b are integers, p is a prime, and l rise from 0 to p-1.
For example, given a = 2, b = 3, c = 1, p = 5, the answer will be L(1, 5) + L(6, 5) + L(15, 5) + L(28, 5) + L(45, 5) = 1.
Hope you success!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1790597944977586874253807693862105869090831146775433873365574331834751726019209506591442208078773976241473125928462255662698742508715860404594308483642903795378308167676299040153811818697911451702904445154302129386511123953430107313631134947166796023035924915773861491813723615347818175385400427140808808322283386297665768154242214499222952216489331176680010590146265347449725494126355357513024142637328595436229897644863168397196581970620448841225319796356036639245123816557559954488007742087175151105860858455715116363238852440092003309715738963596669744460038151717733567857151923644634962547292536052005979807412 * l**2 + 84630915036470848127336848551862837377338010999328414571781592617947609816635217549607977480287704658645062489617864219383977193762675800881689023798012302722595309322292930306616482299614509329833697616277657524866214567038766616558619183553947783922145151789252432700188722287046417136447520620477221941086 * l + 1
p = 78071154667666786921065989577715454710128750240598842469132116007486844604315869956194255914126441698799378564658404581628706536271021788543744520917380601876339806993777200252818764895209123028182167519087251191560071113908062557503168592878907337963433278192224324131644984120467238737663847330953082109397 (1023 bits)
> Type your answer: exp:
from hashlib import sha256
import random
from pwn import *
import string
from Crypto.Util.number import *
import re
def L(n, p):
res = pow(n, (p - 1) // 2, p)
if res == p - 1:
return -1
return res
dir = string.ascii_letters + string.digits
conn = remote("59.110.20.54", 3042)
conn.recvuntil(b'sha256(XXXX+')
salt = conn.recv(16).strip().decode()
conn.recvuntil(b') == ')
hash = conn.recv(64).strip().decode()
while True:
rand_str = (''.join([random.choice(dir) for _ in range(4)])) + salt
if sha256(rand_str.encode()).hexdigest() == hash:
print("",rand_str[:4])
conn.sendlineafter(b'Give me XXXX:', rand_str[:4])
break
#conn.interactive()
conn.recvuntil(b'Hope you success!\n')
_ = [conn.recvline() for _ in range(3)]
for _ in range(10):
a, _, b, _ = re.findall(r'\d+', conn.recvline().decode())
a, b = int(a), int(b)
p = int(re.findall(r'\d+', conn.recvline().decode())[0])
if (b**2 - 4 * a) % p == 0:
conn.sendlineafter(b'> Type your answer: ', str((p - 1) * L(a, p)))
else:
conn.sendlineafter(b'> Type your answer: ', str(-L(a, p)))
res = conn.recvline()
if b'Next challenge' in res:
_ = [conn.recvline() for _ in range(3)]
else:
print(res)
break
print(conn.recv())
#SYC{G00d!_u_4r3_Qu33n_0f_Quadratic}来自偶像的解法(这个太猛了,真的学到了学到了!):
题目后来进行了update,对L函数进行了详细说明,也就是勒让德符号:

那么再看之前题目的例子就没问题了,回传p-1也是正确的。题目更新后还做了如下修改:
-
-
增加了三轮,现在需要通过十轮才有flag
-
当然这个需要十轮是做出来才知道的。
from Crypto.Util.number import *
import random
from gmpy2 import *
from tqdm import *
def calcsum(a,b,c,p):
sum = 0
for i in range(0,p):
temp = a*i**2+b*i+1
if(powmod(temp,(p-1)//2,p) == 1):
sum += 1
elif(powmod(temp,(p-1)//2,p) == p-1):
sum += -1
else:
sum += 0
return sum
for i in range(10):
p = getPrime(18)
a = random.randint(1,p-1)
b = random.randint(1,p-1)
c = 1
print(powmod(a,(p-1)//2,p),calcsum(a,b,c,p))1 -1
1 -1
1 -1
224176 1
212668 1
207012 1
146406 1
141936 1
216036 1
1 -1然后就会发现:L函数的求和结果仅与a是否是模p下的二次剩余有关。如果a是模p下的二次剩余,求和结果为-1;否则为1。
当然还要考虑一种特殊情况,给的a、b均满足a是二次剩余,且满足下面的完全平方式:
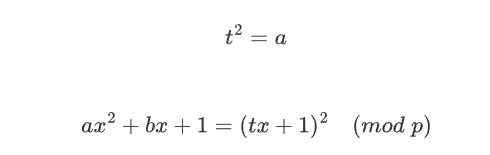
我们用如下方法来核验是否能构成完全平方式:
(b*inverse(2,p))**2 % p == a%p所以我们每次用以下条件语句,选择发送对应的求和结果给靶机就行:
if((b*inverse(2,p))**2 % p == a%p):
res = p-1
elif(pow(a,(p-1)//2,p) == 1):
res = -1
else:
res = 1exp:
from Crypto.Util.number import *
from pwn import *
from tqdm import *
from hashlib import sha256
import re
#context.log_level = 'debug'
#part1 proof
def proof_of_work():
table = string.digits + string.ascii_letters
temp = r.recvuntil(b"sha256(XXXX+")
temp = r.recvline()
suffix = temp[:16].decode()
hex1 = temp[20:].strip().decode()
for i in tqdm(table):
for j in table:
for k in table:
for m in table:
temp1 = i+j+k+m
if(sha256((temp1+suffix).encode()).hexdigest() == hex1):
r.sendline(temp1.encode())
return
r = remote("59.110.20.54",3042)
proof_of_work()
#part2 calculate
def find_coeffcients(expression):
# 定义匹配系数的正则表达式
pattern = re.compile(r'(-?\d+)\s*\*\s*l\*\*2|(-?\d+)\s*\*\s*l|(-?\d+)')
# 使用findall方法找到匹配的所有项
matches = pattern.findall(expression)
# 将匹配结果转换为整数并存储在列表中
coefficients = [int(match[0] or match[1] or match[2]) for match in matches]
return coefficients
def find_p(equation):
pattern = re.compile(r'\b\d+\b')
# 使用search方法找到匹配的第一个数字
match = pattern.search(equation)
p_value = int(match.group())
return p_value
r.recvuntil(b"|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||")
for i in trange(10):
r.recvuntil(b"|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||")
r.recvline()
r.recvline()
temp = r.recvline().strip().decode()
a,b,c = find_coeffcients(temp)
p = find_p(r.recvline().strip().decode())
#print("a,b,c,p = "+str(a)+","+str(b)+","+str(c)+","+str(p))
r.recvuntil(b"> Type your answer:")
if((b*inverse(2,p))**2 % p == a%p):
res = p-1
elif(pow(a,(p-1)//2,p) == 1):
res = -1
else:
res = 1
r.sendline(str(res).encode())
r.recvline()
r.recvline()
r.recvline()
r.recvline()
print(r.recvline())
#SYC{G00d!_u_4r3_Qu33n_0f_Quadratic}Diligent_Liszt
https://en.wikipedia.org/wiki/Discrete_logarithm
查看代码
import gmpy2 as gp
import random
from Crypto.Util.number import *
DEBUG = False
flag = b"SYC{Al3XEI_FAKE_FLAG}"
assert flag.startswith(b"SYC")
nbits = 512
g = 3
def gen_p_1(digit):
primes = []
pri = 1
while(len(primes)<100):
pri = gp.next_prime(pri)
primes.append(int(pri))
while True:
count = 2
while count < 2**digit:
count *= random.choice(primes)
count += 1
if(gp.is_prime(count)):
return count
p,q,r = [gen_p_1(nbits) for _ in "pqr"]
n = p*q*r
x = bytes_to_long(flag)
y = gp.powmod(g,x,n)
print("p = {}".format(p))
print("q = {}".format(q))
print("r = {}".format(r))
print("y = {}".format(y))
if DEBUG:
print("x = {}".format(x))
'''
p = 1068910928091265978478887270179608140018534288604159452828300604294675735481804963679672853224192480667904101881092533866322948043654533322038484907159945421
q = 1711302770747802020613711652777299980542669713888988077474955896217408515180094849053961025086865697904731088087532944829046702427480842253022459937172565651
r = 132969813572228739353704467775972551435751558645548804253458782569132362201099158857093676816706297676454547299888531536236748314013888413096371966359860637
y = 5385116324746699759660077007129548063211490907227715474654765255668507958312745677683558789874078477569613259930365612562164095274660123330458355653249805062678976259429733060364358954180439218947514191603330532117142653558803034110759332447742304749985874760435453594107494324797235909651178472904825071375135846093354526936559640383917210702874692725723836865724807664892994298377375580807917514349966834376413176898806591411038129330967050554114677719107335006266
'''我的解答:
阅读代码,发现关键点:
def gen_p_1(digit):
primes = []
pri = 1
while(len(primes)<100):
pri = gp.next_prime(pri)
primes.append(int(pri))
while True:
count = 2
while count < 2**digit:
count *= random.choice(primes)
count += 1
if(gp.is_prime(count)):
return count生成的素数是由较小的数相乘构成,并加一得到的。一般称这种数为光滑数
y = gp.powmod(g,x,n)
flag即x,是指数,离散对数问题
联想到光滑数
我们可以对:
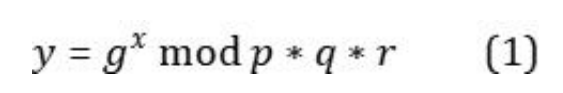
模上p得到:
![]()
之后鉴于模数为光滑数。使用sagemath求离散对数
p = 1068910928091265978478887270179608140018534288604159452828300604294675735481804963679672853224192480667904101881092533866322948043654533322038484907159945421
q = 1711302770747802020613711652777299980542669713888988077474955896217408515180094849053961025086865697904731088087532944829046702427480842253022459937172565651
r = 132969813572228739353704467775972551435751558645548804253458782569132362201099158857093676816706297676454547299888531536236748314013888413096371966359860637
y = 5385116324746699759660077007129548063211490907227715474654765255668507958312745677683558789874078477569613259930365612562164095274660123330458355653249805062678976259429733060364358954180439218947514191603330532117142653558803034110759332447742304749985874760435453594107494324797235909651178472904825071375135846093354526936559640383917210702874692725723836865724807664892994298377375580807917514349966834376413176898806591411038129330967050554114677719107335006266
y=y%p
g = 3
h2p = Zmod(p)(y)
gp = Zmod(p)(g)
print(h2p.log(gp))
#10611516989504525712597368786937786671609696614143113241754963687897074368833799765059908989然后求解flag
from Crypto.Util.number import long_to_bytes
m = 10611516989504525712597368786937786671609696614143113241754963687897074368833799765059908989
print(long_to_bytes(m))
#SYC{D1scr3te_L0g_W1th_Mult1pl3_pr1m35}偶像的解法:
题目中三个数均满足p-1光滑,那么如果不给p、q、r分别的值也能分解出来。既然直接给了,那就分开用pohlig-hellman求DLP后再crt起来就好。
exp:
from Crypto.Util.number import *
from sympy.ntheory.modular import crt
p = 1068910928091265978478887270179608140018534288604159452828300604294675735481804963679672853224192480667904101881092533866322948043654533322038484907159945421
q = 1711302770747802020613711652777299980542669713888988077474955896217408515180094849053961025086865697904731088087532944829046702427480842253022459937172565651
r = 132969813572228739353704467775972551435751558645548804253458782569132362201099158857093676816706297676454547299888531536236748314013888413096371966359860637
y = 5385116324746699759660077007129548063211490907227715474654765255668507958312745677683558789874078477569613259930365612562164095274660123330458355653249805062678976259429733060364358954180439218947514191603330532117142653558803034110759332447742304749985874760435453594107494324797235909651178472904825071375135846093354526936559640383917210702874692725723836865724807664892994298377375580807917514349966834376413176898806591411038129330967050554114677719107335006266
g = 3
xp = discrete_log(mod(y,p),mod(g,p))
xq = discrete_log(mod(y,q),mod(g,q))
xr = discrete_log(mod(y,r),mod(g,r))
n = [p-1,q-1,r-1]
c = xp,xq,xr
M = crt(n,c)[0]
print(long_to_bytes(int(M)))
#SYC{D1scr3te_L0g_W1th_Mult1pl3_pr1m35}card_game
AL3XEI送给了你这个游戏的关键数据,你能预测接下来要出的牌吗 nc 59.110.20.54 4953
cards.py
查看代码
Heart = [
'''
┌─────────┐
│ A │
│ │
│ ♥ │
│ │
│ A │
└─────────┘''',
'''
┌─────────┐
│ 2 │
│ │
│ ♥ │
│ │
│ 2 │
└─────────┘''',
'''
┌─────────┐
│ 3 │
│ │
│ ♥ │
│ │
│ 3 │
└─────────┘''',
'''
┌─────────┐
│ 4 │
│ │
│ ♥ │
│ │
│ 4 │
└─────────┘''',
'''
┌─────────┐
│ 5 │
│ │
│ ♥ │
│ │
│ 5 │
└─────────┘''',
'''
┌─────────┐
│ 6 │
│ │
│ ♥ │
│ │
│ 6 │
└─────────┘''',
'''
┌─────────┐
│ 7 │
│ │
│ ♥ │
│ │
│ 7 │
└─────────┘''',
'''
┌─────────┐
│ 8 │
│ │
│ ♥ │
│ │
│ 8 │
└─────────┘''',
'''
┌─────────┐
│ 9 │
│ │
│ ♥ │
│ │
│ 9 │
└─────────┘''',
'''
┌─────────┐
│10 │
│ │
│ ♥ │
│ │
│ 10│
└─────────┘''',
'''
┌─────────┐
│ J │
│ │
│ ♥ │
│ │
│ J │
└─────────┘''',
'''
┌─────────┐
│ Q │
│ │
│ ♥ │
│ │
│ Q │
└─────────┘''',
'''
┌─────────┐
│ K │
│ │
│ ♥ │
│ │
│ K │
└─────────┘''',
]
Spade = [
'''
┌─────────┐
│ A │
│ │
│ ♠ │
│ │
│ A │
└─────────┘''',
'''
┌─────────┐
│ 2 │
│ │
│ ♠ │
│ │
│ 2 │
└─────────┘''',
'''
┌─────────┐
│ 3 │
│ │
│ ♠ │
│ │
│ 3 │
└─────────┘''',
'''
┌─────────┐
│ 4 │
│ │
│ ♠ │
│ │
│ 4 │
└─────────┘''',
'''
┌─────────┐
│ 5 │
│ │
│ ♠ │
│ │
│ 5 │
└─────────┘''',
'''
┌─────────┐
│ 6 │
│ │
│ ♠ │
│ │
│ 6 │
└─────────┘''',
'''
┌─────────┐
│ 7 │
│ │
│ ♠ │
│ │
│ 7 │
└─────────┘''',
'''
┌─────────┐
│ 8 │
│ │
│ ♠ │
│ │
│ 8 │
└─────────┘''',
'''
┌─────────┐
│ 9 │
│ │
│ ♠ │
│ │
│ 9 │
└─────────┘''',
'''
┌─────────┐
│10 │
│ │
│ ♠ │
│ │
│ 10│
└─────────┘''',
'''
┌─────────┐
│ J │
│ │
│ ♠ │
│ │
│ J │
└─────────┘''',
'''
┌─────────┐
│ Q │
│ │
│ ♠ │
│ │
│ Q │
└─────────┘''',
'''
┌─────────┐
│ K │
│ │
│ ♠ │
│ │
│ K │
└─────────┘''',
]
Diamond = [
'''
┌─────────┐
│ A │
│ │
│ ♦ │
│ │
│ A │
└─────────┘''',
'''
┌─────────┐
│ 2 │
│ │
│ ♦ │
│ │
│ 2 │
└─────────┘''',
'''
┌─────────┐
│ 3 │
│ │
│ ♦ │
│ │
│ 3 │
└─────────┘''',
'''
┌─────────┐
│ 4 │
│ │
│ ♦ │
│ │
│ 4 │
└─────────┘''',
'''
┌─────────┐
│ 5 │
│ │
│ ♦ │
│ │
│ 5 │
└─────────┘''',
'''
┌─────────┐
│ 6 │
│ │
│ ♦ │
│ │
│ 6 │
└─────────┘''',
'''
┌─────────┐
│ 7 │
│ │
│ ♦ │
│ │
│ 7 │
└─────────┘''',
'''
┌─────────┐
│ 8 │
│ │
│ ♦ │
│ │
│ 8 │
└─────────┘''',
'''
┌─────────┐
│ 9 │
│ │
│ ♦ │
│ │
│ 9 │
└─────────┘''',
'''
┌─────────┐
│10 │
│ │
│ ♦ │
│ │
│ 10│
└─────────┘''',
'''
┌─────────┐
│ J │
│ │
│ ♦ │
│ │
│ J │
└─────────┘''',
'''
┌─────────┐
│ Q │
│ │
│ ♦ │
│ │
│ Q │
└─────────┘''',
'''
┌─────────┐
│ K │
│ │
│ ♦ │
│ │
│ K │
└─────────┘''',
]
Club = [
'''
┌─────────┐
│ A │
│ │
│ ♣ │
│ │
│ A │
└─────────┘''',
'''
┌─────────┐
│ 2 │
│ │
│ ♣ │
│ │
│ 2 │
└─────────┘''',
'''
┌─────────┐
│ 3 │
│ │
│ ♣ │
│ │
│ 3 │
└─────────┘''',
'''
┌─────────┐
│ 4 │
│ │
│ ♣ │
│ │
│ 4 │
└─────────┘''',
'''
┌─────────┐
│ 5 │
│ │
│ ♣ │
│ │
│ 5 │
└─────────┘''',
'''
┌─────────┐
│ 6 │
│ │
│ ♣ │
│ │
│ 6 │
└─────────┘''',
'''
┌─────────┐
│ 7 │
│ │
│ ♣ │
│ │
│ 7 │
└─────────┘''',
'''
┌─────────┐
│ 8 │
│ │
│ ♣ │
│ │
│ 8 │
└─────────┘''',
'''
┌─────────┐
│ 9 │
│ │
│ ♣ │
│ │
│ 9 │
└─────────┘''',
'''
┌─────────┐
│10 │
│ │
│ ♣ │
│ │
│ 10│
└─────────┘''',
'''
┌─────────┐
│ J │
│ │
│ ♣ │
│ │
│ J │
└─────────┘''',
'''
┌─────────┐
│ Q │
│ │
│ ♣ │
│ │
│ Q │
└─────────┘''',
'''
┌─────────┐
│ K │
│ │
│ ♣ │
│ │
│ K │
└─────────┘''',]task.py
查看代码
from Crypto.Util.number import *
from cards import Heart, Spade, Club, Diamond
from secret import flag
def choose_card(num):
x = (num>>5)%4
if x == 0:
return (Heart[(num>>6)%13]), 'Heart'
if x%4 == 1:
return (Spade[(num>>6)%13]), 'Spade'
if x%4 == 2:
return (Diamond[(num>>6)%13]), 'Diamond'
else:
return (Club[(num>>6)%13]), 'Club'
def GAME():
banner = '''
#### ## ##### ##### #### ## # # ######
# # # # # # # # # # # # ## ## #
# # # # # # # # # # # ## # #####
# ###### ##### # # # ### ###### # # #
# # # # # # # # # # # # # # #
#### # # # # ##### #### # # # # ######
'''
print(banner)
meum = '''option:
1: start game
2: get hint
3: exit
'''
print(meum)
while True:
print('input your option: ', end='')
your_input = input()
if your_input == '1':
n = getPrime(36)
m = getPrime(16)
c = getPrime(16)
seed = getPrime(36)
out = seed
round = 0
score = 0
res = []
while True:
round += 1
res = []
print(f'round:{round}')
print(f'score:{score}')
for i in range (3):
out = (out*m+c)%n
res.append(out)
if round == 1:
for i in res:
card, suit = choose_card(i)
print(card)
elif round==2 or round==3: #gift
for i in res:
card, suit = choose_card(i)
print(card)
print(f'gift: {res}')
else:
cards = []
suits = []
for i in range(len(res)):
card, suit = choose_card(res[i])
cards.append(card)
suits.append(suit)
print("Give me your guess: (example: Heart_1 Club_2 Diamond_3)")
try:
g_1, g_2, g_3 = input().split()
g_1, g_2, g_3 = g_1.split('_'), g_2.split('_'), g_3.split('_')
except ValueError:
print("Please enter in the correct format.")
return
if (g_1[0] == suits[0] and g_1[1] == cards[0][15]) and (g_2[0] == suits[1] and g_2[1] == cards[1][15]) and (g_3[0] == suits[2] and g_3[1] == cards[2][15]):
for i in cards:
print(i)
print("Congratulations! You matched the cards!")
score += 1
else:
for i in cards:
print(i)
print("Try again!")
if score == 50:
print('The flag is your reward!')
print(flag)
return
else:
continue
if your_input == '2':
print("Have you ever heard of LCG?")
if your_input == '3':
break
if __name__ == '__main__':
GAME()我的解答:
祖传脚本解seed a b n
然后写交互就行
from functools import reduce
from Crypto.Util.number import *
from sympy import *
from cards import Heart, Spade, Club, Diamond
from pwn import *
import re
import time
def choose_card(num):
x = (num >> 5) % 4
if x == 0:
return (Heart[(num >> 6) % 13]), 'Heart_'
if x % 4 == 1:
return (Spade[(num >> 6) % 13]), 'Spade_'
if x % 4 == 2:
return (Diamond[(num >> 6) % 13]), 'Diamond_'
else:
return (Club[(num >> 6) % 13]), 'Club_'
def crack_unknown_increment(states, modulus, multiplier):
increment = (states[1] - states[0]*multiplier) % modulus
return modulus, multiplier, increment
def crack_unknown_multiplier(states, modulus):
multiplier = (states[2] - states[1]) * \
inverse(states[1] - states[0], modulus) % modulus
return crack_unknown_increment(states, modulus, multiplier)
def crack_unknown_modulus(states):
diffs = [s1 - s0 for s0, s1 in zip(states, states[1:])]
zeroes = [t2*t0 - t1*t1 for t0, t1, t2 in zip(diffs, diffs[1:], diffs[2:])]
modulus = abs(reduce(gcd, zeroes))
factors = factorint(modulus)
while not isprime(modulus): # 注意这里N刚开始有可能不是素数导致后面无法求出逆元
for prime, order in factors.items():
if prime.bit_length() > 128:
continue
modulus = modulus / prime**order
multiplier = (states[2] - states[1]) * \
inverse(states[1] - states[0], modulus) % modulus
increment = (states[1] - states[0]*multiplier) % modulus
seed = ((states[0] - increment) * invert(multiplier, modulus) % modulus)
return modulus, multiplier, increment, seed
io = remote("59.110.20.54", 4953)
io.recvuntil(b"input your option: ")
io.sendline(b'1')
io.recvuntil(b"gift:")
gift = list(map(int,io.recvline().decode().strip().replace("[", "").replace("]",
"").split(", ")))
io.recvuntil(b"gift:")
gift += list(map(int,io.recvline().decode().strip().replace("[",
"").replace("]", "").split(", ")))
payload = []
modulus, multiplier, increment, seed = crack_unknown_modulus(gift)
print('A = '+str(multiplier))
print('B = '+str(increment))
print('N = '+str(modulus))
print('seed =' + str(seed))
res = []
print(gift)
for i in range(666):
seed = (seed*multiplier+increment) % modulus
res.append(seed)
print(res)
pattern = re.compile("\w+")
for i in range(6,len(res)):
card = choose_card(res[i])
payload.append(card[1]+pattern.findall(card[0])[0])
print(payload)
for i in range(666):
time.sleep(0.05)
io.recvuntil(b"round:")
io.recvline()
score = io.recvline()
print(score)
io.recvuntil(b"Give me your guess")
io.recvline()
io.sendline((payload[i*3]+" "+payload[i*3+1]+" "+payload[i*3+2]).encode())
if b'49' in score:
print(io.recvall().decode())
#SYC{lcg_a@@@@@ttack}记得脚本和附件放在一起。
偶像的解法(讲的很详细):
题目任务是这样的,给我们提供了三个选项,但是其实只有输入1有用。输入1后会发生:
在第二轮和第三轮,会额外给出这一轮的三个数的值
而根据数字得到牌的计算方式choose_card(num)是题目给了我们的,所以目标就是得到LCG的每一轮的三个数的值。而我们有第二轮和第三轮的共六个LCG的数字序列。那么就可以完全复原LCG的各个参数m、c、n,接着往后预测就可以了。
有一点需要注意,每一次发送的形式应该是如下:
(example: Heart_1 Club_2 Diamond_3)注意到牌的数字是这么取的:
cards[0][15]也就是每张牌的第十五个字符。比如对于A:
'''
┌─────────┐
│ A │
│ │
│ ♥ │
│ │
│ A │
└─────────┘'''第十五个字符就恰好是A。然而对于10就不太一样了:
'''
┌─────────┐
│10 │
│ │
│ ♥ │
│ │
│ 10│
└─────────┘'''其第十五个字符应该是0。所以要留意一下这个小细节。猜错了也没啥!也不会退出。只要够50分就可以。
exp:
from Crypto.Util.number import *
from pwn import *
from tqdm import *
from gmpy2 import powmod
#context.log_level = 'debug'
def solve_LCG(sequence):
c1,c2,c3,c4,c5,c6 = sequence
t1 = c2-c1
t2 = c3-c2
t3 = c4-c3
t4 = c5-c4
T1 = t4*t2 - t3*t3
T2 = t3*t1 - t2*t2
n = GCD(T1,T2)
for i in range(2,1000):
while(n % i == 0):
n //= i
m = inverse((c2-c1),n)*(c3-c2) % n
c = (-m*c2 + c3) % n
return m,c,n
def getnext(out,m,c,n):
next_out = [out[-1]]
for i in range(3):
next_out.append((m*next_out[-1]+c)%n)
return next_out[1:]
def gen_card(out):
table_num = ["A","2","3","4","5","6","7","8","9","0","J","Q","K"]
table_suits = ['Heart','Spade','Diamond','Club']
res = ""
for i in out:
suits_order = (i >> 5) % 4
num_order = (i >> 6) % 13
res += (table_suits[suits_order] + "_" + table_num[num_order] + " ")
return res
sequence = []
r = remote("59.110.20.54",4953)
r.recvuntil(b"input your option:")
r.sendline(b"1")
r.recvuntil(b"gift: ")
sequence += eval(r.recvline().decode().strip())
r.recvuntil(b"gift: ")
sequence += eval(r.recvline().decode().strip())
m,c,n = solve_LCG(sequence)
out = getnext(sequence,m,c,n)
res = gen_card(out)
r.recvuntil(b"(example: Heart_1 Club_2 Diamond_3)")
r.sendline(res.encode())
for i in trange(49):
out = getnext(out,m,c,n)
res = gen_card(out)
r.recvuntil(b"(example: Heart_1 Club_2 Diamond_3)")
r.sendline(res.encode())
r.recvuntil(b"The flag is your reward!")
r.recvline()
print(r.recvline())
#SYC{lcg_a@@@@@ttack}第四波题目
EzComplex
And u, my friend: Complex factors! (In a double sense)
#sage9.3
from Crypto.Util.number import *
flag = b'FAKE{Do_You_know_Complex_numbers}'
p = random_prime(1 << 384)
q = random_prime(1 << 384)
n = p * q
e = 0x10001
N = pow(p, 2) + pow(q, 2)
m = bytes_to_long(flag)
c = pow(m,e,n)
print(c)
print(N)
'''
122977267154486898127643454001467185956864368276013342450998567212966113302012584153291519651365278888605594000436279106907163024162771486315220072170917153855370362692990814276908399943293854077912175867886513964032241638851526276
973990451943921675425625260267293227445098713194663380695161260771362036776671793195525239267004528550439258233703798932349677698127549891815995206853756301593324349871567926792912475619794804691721625860861059975526781239293017498
'''我的解答:
已知N如下:
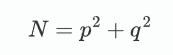
结合题目名字complex,我们可以把N放在复数域中分解,由以下公式可知:
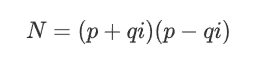
通过遍历所有可能的因子从而得到p和q。
exp:
#sage
c=122977267154486898127643454001467185956864368276013342450998567212966113302012584153291519651365278888605594000436279106907163024162771486315220072170917153855370362692990814276908399943293854077912175867886513964032241638851526276
N=973990451943921675425625260267293227445098713194663380695161260771362036776671793195525239267004528550439258233703798932349677698127549891815995206853756301593324349871567926792912475619794804691721625860861059975526781239293017498
Zn = ZZ[i](N)
for d in divisors(Zn):
p, q = map(int, d)
if is_prime(p) and is_prime(q) and d.norm() == N:
print(p)
print(q)
break
#8732781022306464325787401448517171026218291389436971731700810979177651389459896422549428444142746055523338740248707
#29962125885196559918101088622575501736433575381042696980660846307183241725227137854663856022170515177120773072848343from Crypto.Util.number import *
import gmpy2
p=8732781022306464325787401448517171026218291389436971731700810979177651389459896422549428444142746055523338740248707
q=29962125885196559918101088622575501736433575381042696980660846307183241725227137854663856022170515177120773072848343
c=122977267154486898127643454001467185956864368276013342450998567212966113302012584153291519651365278888605594000436279106907163024162771486315220072170917153855370362692990814276908399943293854077912175867886513964032241638851526276
print(long_to_bytes(int(pow(c, gmpy2.invert(0x10001, (p - 1) * (q - 1)), p * q))))
#SYC{D0_you_like_r41n?_i_pref3r_R1_ng}ext^7gcd
题目链接:nc 59.110.20.54:1789 (下sagemath! 不下的统统发配到安东星当嘿奴!)
我的解答:
依然没有附件,连接靶机过256
import hashlib
dic = 'abcdefghijklmnopqrstuvwxyz1234567890ABCDEFGHIJKLMNOPQRSTUVWXYZ'
for a in dic:
for b in dic:
for c in dic:
for d in dic:
t =str(a)+str(b)+str(c)+str(d)+'ou10Ns0k1A034Cwq'
m = (hashlib.sha256(t.encode())).hexdigest()
if m[:64] == '199ed4b6e20efdc9a148aa3202baac863a582a36ce291172e1399303c1ff7cf7':
print(t)
break
#CzkVou10Ns0k1A034Cwqsha256(XXXX+ou10Ns0k1A034Cwq) == 199ed4b6e20efdc9a148aa3202baac863a582a36ce291172e1399303c1ff7cf7
Give me XXXX: CzkV
Right!
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hi Crypto-ers! AL3XEI here. Solving extended gcd over 2 primes can be easy, but what about 7 primes?
primes : [20406879494317869854093346233445023568619, 13100512001018519103944314227653297235913, 21305878463564524034489535414675952143437, 18784496449134185269414007485289163111667, 21385370626036171764407570115381203117909, 20048660904961039332304848616206835715819, 16245651292691706440662510693345375727453] ( 134 bits )
Give me a0,...a5,a6: 题目要求我们对a0,...a5,a6这7个素数求出扩展欧几里得的结果,也就是需要满足公式:
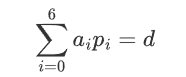
其中d是7个素数的最大公约数,所以知道就是1。经过测试发现不能发送0给靶机。
那么,我们可以首先对前六个数两两使用exgcd,使得:
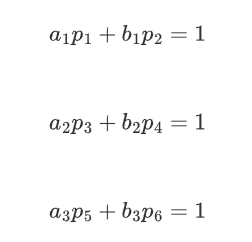
可得到

然后再将3与最后一个素数a6做exgcd,有:
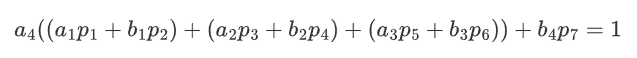
将对应系数发送过去即可。测试发现共有15轮挑战,并且发送的格式是:
a,b,c,d,e,f,g注意:列表省去两边的括号即可。
exp1:
from hashlib import sha256
import random
from pwn import *
import string
from Crypto.Util.number import *
import re
from sympy.solvers.diophantine import diophantine
from sympy import symbols
def mul(x, y):
res = 0
for i in range(len(x)):
res += x[i] * y[i]
return res
dir = string.ascii_letters + string.digits
conn = remote("59.110.20.54", 1789)
conn.recvuntil(b'sha256(XXXX+')
salt = conn.recv(16).strip().decode()
conn.recvuntil(b') == ')
hash = conn.recv(64).strip().decode()
while True:
rand_str = (''.join([random.choice(dir) for _ in range(4)])) + salt
if sha256(rand_str.encode()).hexdigest() == hash:
print("",rand_str[:4])
conn.sendlineafter(b'Give me XXXX:', rand_str[:4])
break
print("pass pow")
t_0 = 3
t_1 = 4
t_2 = 5
t_3 = 6
t_4 = 7
t_5 = 8
vs = symbols("a1, a2, a3, a4, a5, a6, a7", integer=True)
for _ in range(15):
conn.recvuntil("primes : ")
primes = re.findall(r'\d+', conn.recvline().decode())[:-1]
primes = list(map(int, primes))
ans = diophantine(mul(vs, primes) - 1)
ans = eval(str(list(ans)[0]))
conn.sendlineafter("Give me a0,...a5,a6: ", str(ans)[1: -1])
res = conn.recvline()
if b"Good" in res:
continue
else:
break
print(conn.recv())
#SYC{N0t_s0_e4sy_3xtgCd}exp2:
from Crypto.Util.number import *
from pwn import *
from tqdm import *
from hashlib import sha256,sha1
import string
from gmpy2 import gcdext
#context.log_level = 'debug'
def proof_of_work():
table = string.digits + string.ascii_letters
temp = r.recvuntil(b"sha256(XXXX+")
temp = r.recvline()
suffix = temp[:16].decode()
hex1 = temp[20:].strip().decode()
for i in tqdm(table):
for j in table:
for k in table:
for m in table:
temp1 = i+j+k+m
if(sha256((temp1+suffix).encode()).hexdigest() == hex1):
r.sendline(temp1.encode())
return
r = remote("59.110.20.54", 1789)
proof_of_work()
for round in range(15):
r.recvuntil(b'primes :')
primes = eval(r.recvline().strip().decode().split("(")[0])
d,a1,b1 = gcdext(primes[0],primes[1])
d,a2,b2 = gcdext(primes[2],primes[3])
d,a3,b3 = gcdext(primes[4],primes[5])
d,a4,b4 = gcdext(3,primes[6])
t = [int(a1)*int(a4),int(b1)*int(a4),int(a2)*int(a4),int(b2)*int(a4),int(a3)*int(a4),int(b3)*int(a4),int(b4)]
sum1 = 0
for i in range(7):
sum1 += t[i]*primes[i]
r.sendline(str(t)[1:-1].encode())
r.recvline()
r.recvline()
r.recvline()
r.recvline()
print(r.recvline())
#SYC{N0t_s0_e4sy_3xtgCd}Algebra
Recently jrl888 has learned something about groebner_basis.But could U plz help him to sovle his linear algebra homework?
groebnerTask.chall
[175336555462486363373099551411803174933803940918372428249159666803182759268063415863987676455854054651631174131625763475189413468427467197699058719725221879406119373683175842618465694427132003565774900609456204965408254598477034791500576573579131820364396996254469692964946065509325801687720344376041097328929, 192597139210277682598060185912821582569043452465684540030278464832244948354365, 5415723658972576382153559473862560277755192970021711034483296770242757614573901416501357332661976379693731699836578087114136761491831672836130172409491889, 210713951733721296094981135225517096332793112439184310028590576805069783972692891743044656754643189870169698041576462365740899368554671164493356650858567594970345928936103914826926922045852943068526737627918609421198466329605091625, 93558120697660628972553751937347865465963385519812302371069578286123647411810258547153399045605149278436900736665388355004346922404097196048139360206875149390218160164739477798859206611473675859708579299466581718543909912951088772842957187413726251892347470983848602814387339449340072310561011153714207338630]keyTask.chall
{'p': 76231309481023608274751321361920497941621991893430257210800219032855778863403, 'M': [16697564195803960524955618666471317999653475911677692593955332155554421639339, 24805565422829448264880670396335760401288936419812226622903667065319545007990, 30402002570955975554182190550978255206265920770702396357369433463733972557272, 18233447181850080393551606050467637029754113002670714480589747787334593064733, 592902654848011644470609316176765466448791324270572419003746985532591397159, 38141098394328701291718984482265005575605052524114181112646883764482370463339, 19538035520885458475321686600845898258764219979337957736187681124215270558985, 20238271906530455379759697476409410947082642723781332031138364999846953950236, 68589425835163943859976893853743850381901810189392551426919445548155584771402, 69125498641336015332539393144100425718253100049458707350849969745083544909112, .......后面数据太多就不显示了task.sage
查看代码
#utf-8
#sage
import os
from Crypto.Util.number import *
from Crypto.Util.Padding import pad
from secret import flag,e
from functools import reduce
assert reduce(lambda x,y:x&y,[i^3 - 10*i^2 + 31*i - 30==0 for i in e])
LEN = 32
flag = pad(flag,36)
def LongArray(t:list):
return [bytes_to_long(t[i]) for i in range(len(t))]
def BytesArray(t:list):
return [long_to_bytes(t[i]) for i in range(len(t))]
def xor(a, b):
return bytes([a[i%len(a)] ^^ b[i%len(b)] for i in range(max(len(a), len(b)))])
def ArrayXor(a:list,b:bytes):
return [xor(a[i],b) for i in range(len(a))]
def scissors(flag:bytes):
return [flag[i:i+len(flag)//3] for i in range(0, len(flag), len(flag)//3)]
def challenge(m: bytes, bits: int, level: int):
p = getPrime(bits)
M = random_matrix(Zmod(p), LEN).matrix_from_rows_and_columns(range(LEN), range(LEN-level))
c = vector(GF(p), m) * M
return {"p": p, "M": M.list(), "c": c.list()}
def groebner_challenge(m,e):
p = getPrime(1024)
s = sum(m)
c = [pow(m[i],e[i],p) for i in range(3)]
c.insert(0,s)
c.insert(0,p)
return c
key = os.urandom(LEN)
Get_key = challenge(key,256,0x10)
S_bytes = scissors(flag)
C_bytes = ArrayXor(S_bytes,key)
C_long = LongArray(C_bytes)
groebner_challenge = groebner_challenge(C_long,e)
with open('keyTask.chall', 'w') as f:
f.write(f"{Get_key}")
with open('groebnerTask.chall','w') as f:
f.write(f"{groebner_challenge}")我的解答:
分析题目我们可以知道:
在challenge中,将key按照字节来拆分,拆成1x32的向量m,同时生成一个32x16的随机矩阵M以及随机素数p,并返回M及模p下mM的结果c。
flag被拆成三份等长的字节串,而且每一部分都和key进行异或得到C_bytes,并转为列表C_long。
因此三步走战略:一步解challenge得到key,二步解groebner_challenge得到C_long,最后异或得flag。
Part1:一步解challenge得到key
构造格exp
Get_key = {'p': 76231309481023608274751321361920497941621991893430257210800219032855778863403, 'M': [16697564195803960524955618666471317999653475911677692593955332155554421639339, 24805565422829448264880670396335760401288936419812226622903667065319545007990, 30402002570955975554182190550978255206265920770702396357369433463733972557272, 18233447181850080393551606050467637029754113002670714480589747787334593064733, 592902654848011644470609316176765466448791324270572419003746985532591397159, 38141098394328701291718984482265005575605052524114181112646883764482370463339, 19538035520885458475321686600845898258764219979337957736187681124215270558985, 20238271906530455379759697476409410947082642723781332031138364999846953950236, 68589425835163943859976893853743850381901810189392551426919445548155584771402, 69125498641336015332539393144100425718253100049458707350849969745083544909112, 13083949682120928694566559154939525096970647194043481405708057328879273858093, 23203059113121714797053512829874540997525934591781746540284169378085299649376, 22946531388117317614240915936458387347604741596963582908127101794515625023753, 55979468873975052067342467012297454154725653733173077039679834697623008679331, 30639339327762413454972420838209328855396759486202041356245020097084204753692, 72148374844384373140537647811727349763363643424440303708852930034097897492230, 70510577909447876165042155961990008987054640378802283966455273008397938569580, 7816397571019557637378232515822996961951657038149768517938709736489000871357, 71385034180207364002198196251789729137138388141957414602914243475029669555970, 23879618498527644070533133010929524881849183976915843192427726963620597127184, 17735043770749200859447594711305199064407694651519169622831117483831984480389, 23976962869545273044554865578229826802425540170337686767966000016386989130328, 4813526999083764015441613591159575786598306005687621653546973702651642297987, 35706013043056210868734160987149285571667410945166974218110532901324694790051, 61287332127924004349826780222152798665251527987557191801341744495498699149681, 59806212087395698267045456744835084402906230530501342953461649545673934834285, 66657482821382875051224147598709239153115890794174921121727576548156129458938, 69377007797894976274149732824887445461573605559150837203792733121879383465089, 1737071528731565332746911257107778493680445360545221708263762514076835879060, 26379023925512924142330791649751372084816373260080785068747794883981639940564, 39720534772339542897383195711251081371637848641782146840418654967747820062275, 31820568864325484588454986704171504530172236531705504762063219235205599726436, 11412415614112198143545742456902967000465243935062267743559791535435529553163, 32772401021478158811568824426072680656457459212208695033707655574301149228189, 36613809529642944778053478223817784061231181494093237801141665942724705342255, 28439197371291309320639184774010673215730459728641992931504270331352037006301, 49994376135260323921300737379653415875790622538378466317921425504902713119203, 52981071203712051253827242322882615499169952108221727146381229246217507758656, 5368198640133799911534404960909130528742165283715085781170378320545249444728, 71257635543006090454988064080839484336932780804977796104506518470528524267977, 49939544868670555386879967918014313156769501676987773456158169289120020853127, 5513849182743515680002710310848843523475129560643091243794997576549106529466, 30311080181622378163675117234336217803120444223514680794613361255903563546728, 47253144424515535707960287619419823112290982665649838216591721966391572553422, 16575095774038994598908811620087695957027774942428306451930642072988256096088, 47172637987883100907600422604046275130022245811783645092074076667564229591509, 53713237639725683804264174932950491311170902993545808552164800199466276547267, 49487719557414168923381121834394720035219644265706614752390389709105440461013, 25748413371892143171911671353160744041253936659875378210032853927568421372570, 18008028845121322299690631964537137436508497132161626102200990344058453799889, 16865923878308840204551239186825547977455975788266115306396389734737296847085, 19731302167241507517327528775906606230203827145542596977849114707067863875306, 40024901439773791188244711248598957442287420749738843516966316385631890601402, 62075661595095737466614940938346709962838454659631028910757881824583540487566, 20288133589575545550261734425136279824898448287826254319546558610232798725973, 18396337599190064130575563735025697756345644312687861801231441717383177428297, 61662649332383590957920197518379762321289652000599447145306018866100644631766, 47297278799506827936460165998522491497020441120637980131964545819062452000973, 2434481804300022098577582940503850118123308379606916558865314346784339559741, 61460717710239239905767696511877571142159463848530251055586626280454830469072, 38218092905624483835554011371470317993625264372465695584358397202189822877524, 3809308445935104222618133270413897838642480016918582790324761590850768301189, 60169484708414410769331696939509588791672824220639550859073548144342970942988, 15271709649738561680228696342185966023088016417410635809886804641185459695129, 66155017267527705428216922418146119778993818507134962459291676926961980199387, 40582325144361815094579454299209449255300583137755409783698034905476467214705, 7194805288765133581009538431376085998358337085730757398024738539141630962571, 51248452708770457503524460344461222094049441723589286717211964782544227354571, 22498197147885926650572737244750672660840424112765335329871216585556016078622, 19260029934620867188413402870565199213401541118545012025905327078018757276590, 72765401981342793804926955474372068906021406824027837530797739114362593491810, 26557733709775965549141892813261411879509070986449185646889308782249756249916, 75882964734763534706470590708116855183211267542251854842893942812696713968262, 65558131748560689919247533082377923318035739956508689196452998649978595186348, 67829993253688380288988780892768011398698114976114299036143341260518905341737, 16951826980977800861862157989815519885040882739074799726885358140199464697314, 32446755357113992870476957889986702460677003223490414366121640836329037752178, 12249592801055447145409227586142616644156448960361415580962075899504462831768, 67754539010843962660507454221523396504435027352823732054707137518864699178042, 70297827395682032833886772783589786140334218212649181539008979052239234639121, 54916877002052785044471094178468452023757703561016947516347687003813589699916, 69878767045339462957533288607625091900151500688613054221901486304429504671185, 66676699190226984651524622074479431262031540827948817625722859822091518488776, 37343359862502607786043285225073441136188109619529666103637343139525624099037, 69617008840230800774027983202746530662060112473037948560718889791912835927617, 34023459442316105245449622177764320035562291674808673245390486237383753730372, 58836217736932714605695150144545967912160645465028878381545601614754647665960, 59222748784277372772691372984001892824676042244406474647651454241867636982425, 51291183560520843117691150179745095319132263026055872920338388401683396576465, 34161743303094177732273633757443540558673772088482702756673380560373237718795, 34307131145857277718970084816120044947475446756190646647128645192254530721466, 40619186027026335519058147342009392171397856667529112161579765965818461803556, 38969816660406704957262595675482436498421224818936997122425666698567944719644, 40794121792346281796042418182247410063476511606792164833602224462315579047113, 42873094892829318419396887766229282312457081646096347608094509056075735751292, 59931536990963806751890878460380001382300908207154685797724146604005535427389, 26755875060247483082325535695838083770840387919703205792533687755344379394946, 43367143477175416179546646554235024477454387951599453206015050420503396068459, 42786261278310437859972967186896802622955631346091442879938560902191751939666, 32011605834951861381124123053237156531666295421317693417540887608617755500393, 13404880414951683157677928762115608923254793039749942268608296355486752433132, 11877089900228767684891740308804612746605973897075293419611769384342085758411, 27800240708207112469881110853080993649227712650342675861846262212114171421602, 21663581286219835659381271690002813806524703558064974946660379562231450045703, 51974697598961421376559503657823500883117393940660528716837501860648953054355, 6852742579645192782976681029352809589256614923690966236485757863903554035069, 35855739391011276573763391944486554053477241405378310460038837239370814911199, 25499317411645301621939591842312017864107631600944631297145405267790992692014, 5562131306962862994694660621066163309781065393286926932973088057349402319588, 40757942292495250026613925560811211396043227754440416656002665366852555641446, 18002370353172907998059655813638034919853029188826297237387499099629866542454, 39726689200477117673969486403738222570493365361037768374891829430070697803130, 35000135749383571988936158002043170360320337395381038811684971059559128511827, 5641310335570452388651829312936977441078446226495322610431425645339515285489, 60299748799261773479293910979569271438153013125421405725240125178140926053077, 43236034650568428166127856787899498356720414303783169784893885140891897481142, 69522811767745688129234716889716393878934461214025015629400440813257866985926, 62606640448879579972364732068956807349875925982230691648601606744009474947413, 26331285333678560461768318775460827655967933143330152424507184311854947970495, 2615412910278288709156419324276628765375142098301549535618716916032933841018, 1307892460631304569176307753782952310781666613146568927700279439753116859497, 15824651092623867390178475089970118874597630604021225496161544986644731672756, 47659224500120332057240483014529343778388581379297920665421402048441870895252, 51961864134409826142298014140833527652846234416148386918337416218362423427080, 639612686356673570435510441554421795484284145741835048078758652344450124205, 44137808563133710484189150226489053077979585402607831461142023833300560983894, 20115680634645545703803838311574504684652017307676066365011322088032653451054, 23453961374784154821574492914078706218399840238650137887046369876199717640181, 16900806176672163513368898482296275590742399269083482708344531116968904768746, 1033088239828057573934670025891372224995692390599610312154257552196539477228, 37529301212534088685439177351330248471189442148240970641467457998586018600828, 44758658558670428403704358314309089462537518462726001659629731149466886078366, 52531643561197004188179872503729166603975825497103871211472449723704365462397, 39100228068624208345956366306901887462499286634213553058495856303286399680759, 50084656888221865079923599398760080915088064018016395343407634834125281280594, 28032921509707666624060117053276138115957884170215722353372618599407776800318, 57114338186298325807231621434178101761011329483434004023292009415865817538443, 39958000825797431172033845591817417570124784702159857760068966672182242295044, 37975443995963359152259095549178743095281699999555734577840897697983385485508, 3859860826226346586118043402553604028339335048800976779370409309677283839561, 19776331828369039090338830259040913447049235836451080607341980414646928869035, 63362121603058759116851239353365138616548125502014054189583403052688368426366, 8417124938922096613738885001645171001893699423265701100265134643476256258769, 2528187862792013482327567161109437558476612366439226244624203613981198708409, 28439815484745649368170695869546901757055520618328133349460090475484778312430, 52424412563973386715004013697496582995402355069164803452768326078447171945926, 71211964764567865199498719444172950819839102789370908692811892670877437426546, 4852911497761258167355856839166668386535696525032839475042549640021600874463, 12604599543488979007038941486324219160820800119211235264504484549111970215523, 14707627286207296124221923217783940519267566530301202187069927116743690487231, 54982565303499154789362418217587368496636702638346603109876155421010038344010, 8136431912900558221508147412193693425405229437643936872474370939843895786897, 52527332407379202874730182017643715254519386368271623752276320410620277095724, 27007072982620809725787916921614997193231513388215706309009793746137114597486, 8594259875427565483767528869078604778538149152407620311805971227967328114437, 60909592616766854722440243820060988296182888536109613314378246086444257045038, 70469756657760437903499572874961531430585138343307503284848476358837249550050, 33710378649952477094787277011344679479890816598893733081269348946312192670261, 19390620159429311108580146260490873362545571928758643595249797850575767341180, 50247828125873142034313937116587841918115644881259334859484667323061010135147, 30868931184876169045518788073342820415616390474858684405301699072543537570584, 23023240981699193473119197241876724866648360970395806820123980777916962344896, 23996458076167109084834801710867359513927915053490840030842839568905219284982, 18250665434495752390574979184452774394822264315742771513276269170372150019408, 2259977738410451722290072176978139597380420312125626711897728709864167974754, 12986023697223238031523545123890690074279244756420212561751672410792825364360, 54894463714745000972296348237869203583787411196528486760265537862939294199514, 37425912176878184506602309171583658458580304531171364563977595868021237095470, 68817331576859213436304320718837111677416186125049321255877463964380611433706, 41105143390627550033327279192494325897557771670728209002015094922045099669745, 63934928583418713760166225295375893688887003690690081734249993346317611081637, 29228057983414013083385647342360130522058343918940183242873420195035620061919, 51768792160132206523829040289791168367725211511713749754357818583996335222039, 32361017699666327550854675605653538765736862329416095200206293554393607637178, 40771011482807414204888492411092965367622067483466970242712584516125501592354, 24559438367813844616191475087217959641556195075112204920097346901121612022495, 28307745491110198259585972462019261459810520986249892652055646848825309554089, 18111158553544995743378582759414760595774231715148478706446012211834819048094, 28421161206901194269925617922294395794292746509761316483882233546592347136153, 68717406158762870034008809470702721739259380362818921203097329142749903889938, 15229458325589386287270351151382853513665715937106308511729529127964911372448, 14942961257346694397290743531880253247041391520120289699328554993194557045563, 56610619719645794589483526545092427325007943424492457507726642806493936061120, 61838211614666934910392440139437899360325983389254440010643629845091390969426, 1594630207817741980647680371133186282222244195826653301152099379855923258319, 39976143909302683029489041490306637160569309075129062861551966819113272994712, 63198778084454063566056243507718073288176408462904377832506329417703374070146, 12106776746215767660391184528484652896666605094900738362062329429770054842651, 70815365483499881576286614018289560828420950305307679037066862300925666709076, 34155599479028884409904546003583895555808300446163550648895501635054056483243, 47235041940312918011809632710968083587861944792395258754032944720043870810102, 11279460799877672005900296787855603884675607872517313200118064975802612397768, 10336359859053725303799676741278204219230539377055813682550722881699379229861, 24001433259710425078342861846750174290726772095512137488508098310985095212471, 7049674550373684262241332004630735541515205124083507220219609060235158802362, 50293087769094596576302261723136262446101556859234357197374860380714835632857, 55049561539142876216313528082109703360830592009526950861275669253490310828230, 24097757491647814932703635575963958511960435270387057288022919279012109086946, 62905262489519793240906650770706094701433331951407533976510922812426530634545, 69677625747030426028129240089875897587698802269852416057858391413793141342688, 28568799988015882159268699884165479053773466470198251445036573781621473843607, 48908708556147233348205238806248811526907324429222052931112659501432420733124, 75645908390275198838429192800346989316450137989356358514356982597865735402323, 60082563190048351844513479300762813796897774879268024358374332620104411916700, 16523709897084716737459125942868016279469453232477289276516765378562296165668, 63362549505482113440270099262939883171447274797538467413038944520364119516718, 26107425940292159002767387552475149278576449630558985120740293110004090893066, 2267247306370142331449210449023133969505848688804465371976618588938742175446, 4367582349579199965745584849752141603187801405653615613925001523622566142155, 71950093133753953422498906601803601409176253942448831811229176481313428824498, 59491775987458992228501582198728224766265155377250736591884564966816154899032, 60603274794520656742993725195503379914480534517451590572821020343649638467982, 12147679757794683622978226427989986716096751551025993146428355739926944490440, 9564942415680027280124646717782074670637906402338800428864342404989400083620, 27339035075687488604647651353802720326590480574210101944972930375883335285851, 21434270295179865588755759223298333792492764327605227471509726527574957086689, 38036319876998947747610454429574853328747761761359198496585873873948301686420, 34123071012005686047136416507535007458301856373801379312596381262854885103338, 26183449306325954767319451694773007535947028452350445994452962450262785471064, 33912225671968036455962599919081625150047015745659942172123196765629863143907, 35951020632065220561955396698826855129736709222130294457213709880995671352365, 30836911128127329019286649985341735952042155264997267855059287429460149096712, 69532642164321748473696939934926110085832676040501508996027260847608124929604, 10153079878853181057095274259436557838673301706653496304569888904761813085470, 13781625753984300810645757380400487905125752100752372784422127968148437719278, 67291930985685813727718088546813922299729682094604523855004454973224463379803, 70555628333491515495901306613211926697986451987386228309697345524751289035036, 53743776579048239754672091815633123314443157558369350543865632621816227287151, 68625421652391965076401674288319552477262023233333600080736610161381666691851, 68214961525407801292293774810170138395538315813015551932538265610474221437925, 108478603062379448396313690802578260586826385107457547966246050244586889653, 17850962271100788774733904414554594775032031250721378512309666279413256908100, 68401124053423238180932425785116129488963771067777390166978955053650007539174, 41308379551556870522997409220235826506467243065964428705301174356920983269545, 35460642824488567978742178792618486189604188650094694020645470247987130826009, 25927116776772079082443643840095689541439829653643797584560972580282532908317, 58212563959898367356241812575838609781580536191789263916786248567753460941758, 70081019734967724810472594115638455697796383162699658778850210145643708255055, 7318937013937943870960226972389592496964405573483918794866934831052999095028, 16386827908287810251482644751105836326199438044904669871099956113913486870178, 44601873468153349068313548398267810588501004724502949934074832089403404193285, 72365645959522403941725684789269335063058855406738177913754690862646950182843, 16771218590216980015793511028537692767302331361221481854551078801185971964147, 68498727060778643690889786451596469837396689531508387322367175471815038796235, 66505303613456331676754298818965827467846564046903223059321515134065968853381, 14103339333476369027283355473258973594184113562261155164803092812929087041002, 20149458131055400017813548765524380312378326777003730874778166862385843135367, 68362814397144998600704695153849734582744154023993460510385244305799785134657, 15791666226290439600140036379097225268374927472963559010684326326836557581106, 2252185449620911291377871638232740599539417178811979943420436329728757437052, 47698250136447118891314790959404361946127772532616124382854747980926566462430, 23186489809337051714797650239858764600558333074288416924025717609810056163889, 21764163973610747516126692766788224850151405280591445233076316314640271031882, 66189882479675007489330018463567650013283296464749593201753850526987949975416, 18349197902265641400051516596878539099698311348601920279047947082291648764209, 29534326948897865460972990466686282597968037449340555417908148354665508316311, 30761726002018157035512152020110436286407754168906922494902366469595925911547, 53470811125044570210268948746270880051866921377474524419805212771755689494239, 1718252715648064702128922609242974941733557502883869569146315179232997608448, 11387499294072063445562000942173949715804056241643381896707593832669694543533, 73190917948248307878355032820918428667254963054687203377103984221927729107329, 2754924808123516635322508269025982280348732792397898445374737750901419879892, 18392777520533775974331283458268583436805830250170822504575240887864404631258, 339857287167668726475727582116295455303066302702113718887477375482178913131, 11130644489292701093833211174262004002677773443507897198765923801116993268563, 19773468524801403668141715448569907183978558061962367756724671730514045670455, 30179599682305812383092811956530892131229888859754804552480182525253186087395, 62909185436282889899219419098553455168866163819284667959074524718726911872369, 19869570614667900091191055616123563195066117498648951198937139717994004755597, 74449446783591229529843871225569265771129896105452423402241634527178731886684, 63396677289466168962943044108919946383755210323418106557438390439855351241957, 41416147312741810450511037137963580300734196711090158231991707383784713097055, 54229031375784249713712749426113346917158761981749277572353515835808671169487, 38945934412719839619082893176722242458000574495271560956003825693153480739242, 16487090738884862710253652154283588099287933661516349462768417414855385888090, 43826999507232911403929036770652350249567515586351752321814902084933468871660, 3449200793915057262252455796662993918161789556798535902809795058957527335322, 41264121674084026284499114095557145512985657470422997288055899071338699929779, 64472937693232175320174536529491357253649254539383054954009874341776018343642, 74857293754800965593422507277945520778808275948585663404825604191786154926572, 5815401313116918143006631725509484645775007330033782585202345651872053808595, 37197896408873820874244421420831644361849255252055930907806522921208350775039, 64612516161759831629153934495914308735440301897133178083405160557284431288062, 6559843023820545053855833942571567076667408547751733575865753713103768351388, 23437859458185858514664667165353093105305612490482121637480297616471460022122, 20274295990762879799830790571682510221625279103061049956778950817733880775419, 56401143574723504944509185121746644273583780035351217559257907121927365401449, 49601992218738067701189706997135568168476724951148151719915502090514327693221, 341186914486664186771385431945363659110447477400294501019904692883991885913, 35034547603536685580523474143512924804215389058420557699907258381581548447058, 12200305304384520144709999256812132890182568366360405150906949960405768668212, 39082001882692927976859835410233841784024718778286445924310806205861631259877, 31385899040100510914187053148596292409959170884594053055923974443773698154508, 5835333348903500569738395009368766826900599549472035201775438526032338962832, 8073262852355325014634360942318701107854106520655139805022423637269325030952, 15201395730259063595486794416894052687408854909531507923325451061007646348912, 16427855579354233950275414209580340954569134729882232220122584282551493637784, 14939496218250709237679403125346973587984606820530045006556503486993199165868, 11472018317719132922440196176527154420012451882426166339081202168722507006391, 20562533742066382133554315281828262527674049070006798122553867931071494953097, 28524309930702578392587668311431861542844372396686280497129185069949980697887, 28383799886783235181459389725380167461672465671031363872148608556915934650821, 55858389045107938569827040507629525345474103343481046708180317803708122301591, 60130630314358998201961002540806426109698641115312889893545652213850027383317, 62568703748846586914004173002862196100010439494734550299970402141247677564480, 17072350907727140008641307409070995538642452783348448310992620875418467969325, 73713669713737928408393603793843892467892931893611774363620064726094232766451, 74924693780545798658596704166788134541217378161440448755639826167635348817201, 18868660066305006502591849005871664243845115744730952540180642652276775085293, 62340224361267634006286814100182579622129145288096554244391164203193515881749, 39627274282853089038123962325670720421395853551562914127393792454878764135694, 15875125499294992097449915335526612950522181082288770749491670123007795938830, 60347930680219965971015122873223017639063549778786148029298776837851386632197, 34804246576701738787777230859657047300861773235137871724401221304294655339922, 74533835097703506143597441265411820511880172767129948539794601205386044777692, 14313559485096981913264509436614352434539748805581872239992105363481732829367, 19171789603672277177031372245677531017754944212759999350309655106207957804079, 4968175301831692090292608692629174087333895759761745248376489165274706266140, 66639945794581084754753051281751407776097426324318667075086725551710264930290, 59129622729774783807536138073038505378065074618899090268492550568418148993817, 26330600192574911725030253530674667135249314930010022161561110487432679412346, 37881986704920521195794026228790435554661878645607329970186077787030456659000, 27701963450984409765947049999542882575142094924156220225677307089589870028275, 72583659346427605251468432495168368101442353233014061588652475808297035455520, 12989281482076173982092249100245773192037240577774571153957309897342475222983, 53632058799614335393892361774018122602253084706713924599291134300574903019263, 20629095213919844162761775592879555854908917555384903352158192223392004651847, 56964943703372619910676152072775721540805653363005415107771872381562741955707, 68258175306303746182752585969557329490259603293733362129509064175919040300035, 305059625297334113518421210177084300832046195491993511523415230959150990073, 29627101342558600381782480796033532526842782996378655001684599509787200614166, 63083188609616733628410982115889456461165904638544130382266320173120806597633, 26787135105784799411174671164943806509174770974851864542632539666931383923294, 23066937861699903064575204924379799292078776619882229043415335013240639787814, 45667754933572606110898663979907742452417927316570454983599210687471516167897, 14305984325362513624943911776711156769158238069530207305703314765820164002676, 14831302607678136122176302607664477491230563977695179542864281028342301024710, 51037535846798104819405365682536695438509423898887071739014597105930057998419, 48652369650371740655690259282449880747930148169789680102695166437643005057154, 71492013918335334326695792216149984614913026146966017429260406965750804333399, 16867947212719052891303320067120340503543671114624235990428765330449681436, 73153795081830390833986618172943844382356209528553123455517576050355688776421, 29898811131286422521246118406139753008373279313361851068708215082260704285093, 44380753726589115543898536715604464431803358814745567231003254087023278125824, 28108379633113198575413568955011902702769938460938785967518524380028624994265, 28358289655293158986635669238773905207507920781300060436619119106291970359443, 19920848903341336963434902484854707260554671313892340780418153954186042946379, 56404357261193882915914669050476018754919847279836580731159450057153595235354, 26955068855031090885997069113679442709145027634024379353826028271400627789514, 46919410443478545252523437804442059234017614273672686022027209018874653457945, 57974642082462673365757545097294623041253313070904113609253558507159565225848, 62910748878179883431977765511282925445221478599898014034682117091464608104375, 41825434614169389280942233622574957372686523794041804073185538032682171241299, 39176480473345396556027909249429577014354747976864427429163828423143115456346, 50771776778772460180946616763755986966728800933810714726146848203134035578043, 29634833793005329382601833800465647751190159016124488767981549343135828908568, 65535650339630683132316514902898786158169187634011500515811661482049169399011, 14457898428120714622842227300845828676787455966886884216218691279452858037021, 22751967367776513184207196442050134343461085155210009474278586994560117171204, 11729511490772837953955652665227118752756775424188659305364499215253423715438, 15789566757538937158938105539719000408154428860261010255639736638867095964778, 23240445069758350396695618693843563681627830257032646749119379850633259411290, 28242810972693074985503555116117311832919586119574897405101100504865585369240, 47453559192300590466181957141888962772728479360685128165473991527654656435151, 33039215149084714455769343931369837808821001333724496577370451256478328435103, 53952871349034967709708570687453773705342973975753778136392642600234209153958, 71159230176900090188265538027242589769738350211145076037147065381325814851881, 4295733538115639473511178974431656000491458882726394621256091205289071673747, 14836628031793152342428206106649168865191282879949262432290127036712291876402, 2597748403518739298354922786091066021205791271781959146296009797099187165741, 34927392879121980516322010858985102302769920279321437160145901071908795152354, 62245421549208037106736271122570790927624573878669953062980881715450316959314, 34112996342634610342610203612013397815191296698891267550924352771276390156797, 48361745712066250517413636759572062076329188102394048629020763127684453728224, 53397364219490215140533435564047966604689750181018874401158433933226517921900, 25334047344031509427131399230122578099376953527606993887922799651730761451619, 16205160293342452655841185463276242966521391986484484096730292291693250797604, 55563822793939811662468997513054832756010144395623935190537268603584805644827, 22114349202644461306169184577423044992016896956107066824825973217708308287116, 58695735806144401022975804584348837912162125885447517690557802000538437903378, 62725110257332629707399545726290115276445838074720620323269881894812426240679, 72740545121235936460444862790732485876972138180360176807966637248511390202687, 38864922104503648085491022134186410388141363612131609524900163278961538805733, 6247498858902805956542008003425674825514951325194472192178974156108361402749, 30648166516566441693759932456607317547733476012380883874434122970160880247865, 4575334954291461959300238118233126057327760627427519194764502389800603769311, 26723773897526045578700798200406415810129732323809340593034097219007693767854, 6281037362081143841956572043052603650992335167706387748769908464787308468116, 64286047714880861237184633243002930991489966703054078421265395334582627848932, 33818408610159843439047291985292606030182385527908458939427536161601340606500, 13609013542259741479595055902471609005249306799788738033790269414947854732629, 17536333299559413769278779555899593685006959541248796392802972326814918093248, 18542411638263264709758187416205171006507952876914760112442559278337229190468, 31846307469493034316838689952382906549343543129130420785699083222514237248697, 40592429062450574675035536492279226132878508761351666544199201526262149036841, 16070354072152084171251954256965650868127334909410310239796909435959081936546, 66536651726235320716025905422215915536286975298767682203686010158828435836422, 63270779796490661912896864051407657325313990441210502073013713188722504687202, 50652181520504076157357984563735967695339879803377239175496269836395534982946, 69540558045608743280398490296786655030621238466469982991343921076457859892940, 9841051212527423402731044947747280437008712156236340601824643614196211843274, 12072222018009015572844794012125711875706395783186099114640032625144896635637, 72419230614634083225561970387936606863520709109027207928733198765143960628549, 68236958587200491037437084980978920554330839811562873222255335298700415667849, 59331603199698090304807290138357223750101574056412462750232912383849681378085, 74049416996499094867700938158176620507912183088060301485677228398518810315308, 44589211804350556947586393168468085510624406350243223906451657367443079929310, 11722889880704782579636467834320145727215315468978673105078646852644144267302, 37162938201479628318221670413677559400634057715866847284306714513527750674945, 77991069668341617159462711549869846198981640129981167090704944318704115674, 24781325074095957562937506481915752661363803640103881644858900422306288107594, 50243394436655506401651990642654333034843737321908127591211346146733919698702, 4687442095492726629407063506774869319329506588382547411714227663275278730148, 48665673214235643977327797912745435942206989823180516039539449161268668431974, 74131491413435387119131792722727733759321126020981238229557810802823961991702, 47189904836234956626027292138719309126034135335815370939500027177471882713971, 66642336946744336804106101412855565097025008558851680802487967517455789735556, 39100372733134560391249654613242874470306770053063559688335189061474490770670, 36297514610067901982629018660863166180382473936564037667028601317491991540860, 17324149473313481441270662400440503406969190628735911302837720385800561684540, 42802542236449653261447468311512525596146034881422362728317294020745706813252, 25651626139042609821274522801014495194664487121861815773466154842331285580014, 21716541386578074685869691456061206430285733782385055679840762260951476166122, 25118740227793068650697511146427922183350190031672179227128187181026982602852, 6303338362653191359429840875638154590221214529554254398020317282924083430797, 11676823602923092202726518487432133136153160175716928324653897909896417377812, 22591527842537341294483145138410804137744418275229475690901502775329143898600, 15423465169192480181442356594804980261283721927836152132025601291491315262217, 52812609311392879213822230880621473875352775152002161311612738871397605863880, 21901474529203951179264708005591369522295919484211247102532107112869116078257, 19797638480369991652756574723879513200654975293893348736030544826044791556948, 32988016865606803311065174911158930953616176692859261085994695731044998880154, 15013720620266503710552310356736760039787771152262419663931415383640959944255, 53402948699555555850235236503365318293878053556599845866304850886181009545872, 578414726576963854876846913955619952112582994566716072456132976959884676179, 40466349321388782370223373531538345659737923443566152352256589514853112352198, 1880872771817929401422746887732401444754320797361077742359254586522061791227, 12047247386203611116264496398473894119847278156533141745303654172096885251156, 69936255505090807483097726275462417694819398874749133254493672186121798377200, 56189742534184179404452653989780779218184322976165328587052998625929343322623, 52236009337040761579658737818262052113202727822428351125061965646336627100741, 69602156301479647575919598967688239987914479074743572725062043540490654070257, 43275610870271333523729921390330711657817760080756599441857535230607760941411, 74801842670674570366950941554414694286416981233096278329410936531267480474569, 45523293713799774297869620313627743054021694164918818578543266334503113411324, 6224628148872498105530232773778180856237282756455349012259772098459006806701, 56101098821863605404331255553131939303182353871414861601368987041137915588237, 62514080568984452192743867809516234273763360672588340116364253250870707318521, 19649775237337628583259267760455078900133044996026852089604162480150727282031, 2681234746190183559749527177265047256319920111047263024620018491184772138292, 72477724874088708435244260512231062708354748933432591378948353186584708518437, 30252634827911264412522143493887618347186344100498154681798239667087055584973, 62928841586820277215525270906650454728386236998562125216494201758368148279508, 56211379382238646600328517905522392005714296756819673058449743612932975181011, 50094037173696920599812572028124311773584583077682555863904810763866337865415, 35317166218591202676897548502174130503664049068075924052208958517407974181419, 25506065854504640436633838443529482237490038072404045113454162320518595298079, 24598282043408933159434555506241937793897636834036366695267201954251938064858, 40359136257256317951754486181700633715943232386029795075349229741392377893448, 41753903921049595397751509756734177717249754689414242359419638438895614782681, 64879894430542426137516569367284410206800804149311771326329785080288758261071, 31682887186457559477375016497207344351697184042518871050776477362607703713335, 29968228072586790097820746477232816665998277976293252190030364133538849649097, 332255312561919030611963580501150855624827653577824313728984209608512608771, 33823033061488824234179656069812811550521458222627846709618871103804433549208, 40256197078476374288168370733269644672544776862251441956395184831531034573120, 63854791069720406920587264743813005867085205938858782942089091387745143688524, 9599189722183226358779095857498561886058642596617187395926371060462688656609, 15029540387621509138061041056904048961380890903724088755367710335622982174182, 4834678835879134834601247929812861614226805889003245637987605009945117449222, 49032287443959922585421022539339859727864184118407327061056787486660050994804, 51367113126213677371544088617641070281761594598856355289598680348862100934405, 48099687480283705985883062779219537419919474724954533559850612088090057306918, 55520602086715679118869322729503627581286641464273224324645023518549139088388, 50455510074969331802134040882996226109444134111548070407754215749016079079591, 47469806992474607142964806583892893209350327489840529459975202523406918697529, 44993893961585674228825543823064277790256859558754760867449903789983284056192, 44122596973664102569554815809415734634633243724572865236160697307096168452789, 51722296980185400816766674111348260571814278086142919892660507537043249830719, 2033567717312718757627805714157011922823676173550156447506958538133031286918, 40903326746018205875236484413558515226676475499740080681613680228360211918942, 45655754955370338497959237080418596437202658977517625068449957735452901887933, 13099233879696255324623677988804870917874154288631096861534955732046228968134, 44471530296771048523910819473361036714610802054279177471367823293743719275909, 25446261500563608722277325170677124816913924327250182158338980791838121166348, 20849472122256100875237011040249343324234928290319054354358242725759352931027, 7037043514495750961085179755568922433574397862705004833537643401449768094927, 24602719773333598554726432771595598259193579434836329001621386950000691219145, 18291650246498286332477867018368277382676465438496649012143967117655345637528, 45539989423554662584586894487111357151994014405213908150771179299468367899190, 48070107064454632531764035109162049005752680792201710661207400175358438021031, 7593113852866099746235678251926660680184416554718335029164595384991677535670, 61267284459965876196585417165926198770265833151343328469624242730879803451439, 3113616736283221407577816039505851478576505404761990976205583322559028256017, 29330053766980680089057055489775792668017015563299551837945432855633479513403, 38650331327684731179494096039889807053556745918527992295694445248090022667695, 11185985969572649911287822641562854469066291745462641774733857682450748347757, 6571676849591061846860086681136363771968700745359806059302040914080951597505, 47756994940258770519162165424758057472757403664170491681038228297319879170179, 32594475773547428735290676052531964976552484974356093150173758902449423156454, 31898634435507821969130133343503506337057311382300091683049093677942058183477, 8353498532203907327130477695937160917023156103120835230016413595452591896676, 72216190258743114705738161722736218780580609507689664769226245468683927077534, 70887162563386966001868090323354098874355491350818633411742235015483133077695, 53428119825008762677728594318441425057537661648075595012957502970943136262892, 32863943200860906581953022085708385110199346863351756782360531422328330178353, 69608025594463019257125425333532340909708104310858865262120126307135308366029, 33452066316790958427311031033544525015058584636612574435078141485268045480510, 67467748971757982782108778816344194052265871654600993221694391564870705065723, 4109223118757802968784775933084268418756424413308874230869847907255969302298, 874689888905623826173288368495929100158181002920189916388429819486644481023, 72378176399887630170201236756088580064855288788646391253391062547296108569964], 'c': [53988415223839046381660672886792550892557190087087742629543368068682997090947, 21920921577840820689544269317401273370645213368453408007695580910149937697350, 29475771140129436159914858194223947593631108556842828359576509962355002130884, 31590148131791243731394919647376320328981021184223344832519185603844396786591, 40158574856962337545114912732379830254905090560850444592715018068912713975950, 50202503631530908716292345385552528345477433154392551391113477385703155787943, 25774597836388201526898377602793037428257024917440689218589384298072305574879, 63699495213620446235153554941891496976361246452059711453175708378318694602997, 20163212118036162236820095294493608896188807674678722559179017053183514140545, 19274318563716163915370869155502529679348083562418954598176006625003116718683, 61195117146757818795182876923087120232550209256816533077870026077903026793552, 64135143979846412750088422623420891325395709280682206900910074454563319174684, 21787908653560434902963868824798375507100016805476198412260169885990367978999, 8441422610194193525495290892888645173453076691768846248230542826479457290786, 24175440953264371229111128918926940451898832762196824660170198350642339016663, 59119734184764887826210301129920567765450070009167528626807613085641307427339]}
p,M,c = Get_key["p"],Get_key["M"],Get_key["c"]
MM = matrix(ZZ,32,16,M)
E = diagonal_matrix([1]*32)
P = diagonal_matrix([p]*16)
C = matrix(ZZ,c)
L = block_matrix(ZZ,[[MM,E],[P,0],[C,0]])
ML = L.LLL()
key = list(ML[1][16:])
for i in range(len(key)):
key[i] = abs(key[i])
key = bytes(key)
print(key)
#b'\xf1\xea\x1d\xd1\x8d\xec\xc4}\x99y\xf3h\x9d\xfa\xa4\xc5\xf1U\xb8\xf7\x91\x1b\x80\xb8\xcb\xe9h\xc4v\xff\x0c\x18'Part2:二步解groebner_challenge得到C_long
题目已知等式:
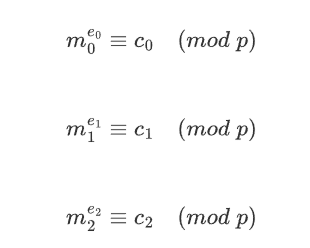
而这三个mi就是C_long中的三部分,需要把它们求出来。
根据
def groebner_challenge(m,e):
p = getPrime(1024)
s = sum(m)
c = [pow(m[i],e[i],p) for i in range(3)]
c.insert(0,s)
c.insert(0,p)
return c我们还知道mi的和:
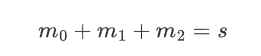
根据
assert reduce(lambda x,y:x&y,[i^3 - 10*i^2 + 31*i - 30==0 for i in e])可知:
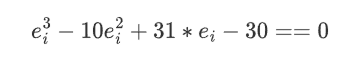
然后sage求解方程得出e
PR.<i> = PolynomialRing(ZZ)
f = i^3 - 10*i^2 + 31*i - 30
res = f.roots()
e = [i[0] for i in res]
print(e)
#[5, 3, 2]因此这个三次方程的根为5,3,2。
知道有三个根了接下来我们对所有可能的3^3=27种e的组合分别求groebner。
发现有一种情况在e分别取2,3,5这个排列的时候可以求出mi。
exp:
groebner_challenge = [175336555462486363373099551411803174933803940918372428249159666803182759268063415863987676455854054651631174131625763475189413468427467197699058719725221879406119373683175842618465694427132003565774900609456204965408254598477034791500576573579131820364396996254469692964946065509325801687720344376041097328929, 192597139210277682598060185912821582569043452465684540030278464832244948354365, 5415723658972576382153559473862560277755192970021711034483296770242757614573901416501357332661976379693731699836578087114136761491831672836130172409491889, 210713951733721296094981135225517096332793112439184310028590576805069783972692891743044656754643189870169698041576462365740899368554671164493356650858567594970345928936103914826926922045852943068526737627918609421198466329605091625, 93558120697660628972553751937347865465963385519812302371069578286123647411810258547153399045605149278436900736665388355004346922404097196048139360206875149390218160164739477798859206611473675859708579299466581718543909912951088772842957187413726251892347470983848602814387339449340072310561011153714207338630]
p,s,c = groebner_challenge[0],groebner_challenge[1],groebner_challenge[2:]
PR.<x1,x2,x3> = PolynomialRing(Zmod(p))
f1 = x1+x2+x3-s
f2 = x1^e[2]-c[0]
f3 = x2^e[1]-c[1]
f4 = x3^e[0]-c[2]
F = [f1,f2,f3,f4]
res = Ideal(F).groebner_basis()
#print(res)
C_long = [175336555462486363373099551411803174933803940918372428249159666803182759268063415863987676455854054651631174131625763475189413468427467197699058719725221879406119373683175842618465694427132003565774900609456204965408254598477034791426984973114319422168794550068252297864611570239554629678043272534782205132762,175336555462486363373099551411803174933803940918372428249159666803182759268063415863987676455854054651631174131625763475189413468427467197699058719725221879406119373683175842618465694427132003565774900609456204965408254598477034791441070070348726882479628953871755257672217743797421672257560044812378339845544,175336555462486363373099551411803174933803940918372428249159666803182759268063415863987676455854054651631174131625763475189413468427467197699058719725221879406119373683175842618465694427132003565774900609456204965408254598477034791441077538064071473846707298910579940788965430025316563097279250948717798654116]
for i in range(3):
C_long[i] = p - C_long[i]
print(C_long[i])
#[73591600464812398195602446186217395100334495269771172009677071841258892196167,59506503230404937884768042382714435292728321711904129430160299563662757483385,59499035515060346517689697343889752175980635484009238590441093427323298674813]利用 long_to_bytes(C_long[i])转化为字节分别得到:
b'\xa2\xb3^\xaa\xd4\x83\xb1"\xf8\x0b\x967\xce\xa3\xe7\xbe\xa8:\xcd\xa8\xf0i\xe5\xe7\x98\xb0+\xbf/\x90yG'
b'\x83\x8f|\xbd\xe1\x95\x9b\x1c\xf5\x1e\x96\n\xef\x9f\xc5\xa9\x9d,\xe7\x96\xfd|\xe5\xda\xb9\x8c\t\xa8\x1a\x86Sy'
b'\x83\x8bB\xbc\xec\x9f\xb0\x18\xeb\x04\xf1j\xef\x9b\xfb\xa8\x90&\xcc\x92\xe3f\x82\xba\xb9\x887\xa9\x17\x8cx}'最后我们异或key就能得到flag了。
key = b'\xf1\xea\x1d\xd1\x8d\xec\xc4}\x99y\xf3h\x9d\xfa\xa4\xc5\xf1U\xb8\xf7\x91\x1b\x80\xb8\xcb\xe9h\xc4v\xff\x0c\x18'
def xor(a, b):
return bytes([a[i%len(a)] ^^ b[i%len(b)] for i in range(max(len(a), len(b)))])
def ArrayXor(a:list,b:bytes):
return [xor(a[i],b) for i in range(len(a))]
C_long = [b'\xa2\xb3^\xaa\xd4\x83\xb1"\xf8\x0b\x967\xce\xa3\xe7\xbe\xa8:\xcd\xa8\xf0i\xe5\xe7\x98\xb0+\xbf/\x90yG',b'\x83\x8f|\xbd\xe1\x95\x9b\x1c\xf5\x1e\x96\n\xef\x9f\xc5\xa9\x9d,\xe7\x96\xfd|\xe5\xda\xb9\x8c\t\xa8\x1a\x86Sy',b'\x83\x8bB\xbc\xec\x9f\xb0\x18\xeb\x04\xf1j\xef\x9b\xfb\xa8\x90&\xcc\x92\xe3f\x82\xba\xb9\x887\xa9\x17\x8cx}']
S_bytes = ArrayXor(C_long,key)
flag = b""
for i in S_bytes:
flag += i[:12] #这里是三份flag 36/3=12
print(flag)
#SYC{You_are_really_algebra_master}GoGoCrypto(比赛期间未解出)
题目链接:http://47.109.106.62:7842/ 带上你的web队友,拿下这道crypto web 题吧!(允许小范围爆破)
这道题最后没出,太难了!需要会一点go语言,赛后询问了偶像,不得不说佬就是佬,真的c的。简单贴一下偶像的方法:
题目文件太多,这里就不全放了。找几个主要的文件信息放一下。
main.go
package main
import (
"GoCode/Controller"
"fmt"
"github.com/gin-gonic/gin"
)
func main() {
fmt.Println("hello world")
REngin := gin.Default()
REngin.Static("/assets", "./assets")
REngin.LoadHTMLGlob("views/*")
registRouter(REngin)
REngin.Run(":7842")
}
func registRouter(r *gin.Engine) {
new(Controller.PubController).Router(r)
}publicController.go
查看代码
package Controller
import (
"GoCode/myfunc"
"github.com/gin-gonic/gin"
"net/http"
"encoding/base64"
"fmt"
)
type PubController struct {
}
var sid []byte
var key []byte
var iv []byte
var nonce []byte
var pwd string
func SendJsonBack(feedback string, check string, c *gin.Context) {
messageMap := map[string]interface{}{
"msg": feedback,
"check": check,
}
c.JSON(http.StatusOK, messageMap)
}
func (pc PubController) Router(pr *gin.Engine) {
pr.GET("/", pc.Room)
pr.POST("/api/dec", pc.MyDec)
pr.POST("/api/check", pc.CheckPwd)
}
func (pc PubController) Room(c *gin.Context) {
sid = Myfunc.GetRandBytes(16)
key = Myfunc.GetRandBytes(16)
iv = Myfunc.GetRandBytes(16)
nonce = Myfunc.GetRandBytes(16)
token, _ := Myfunc.AESEnc(sid, key, iv)
c.SetCookie("token", base64.StdEncoding.EncodeToString(token), 0, "/", "", true, true)
c.SetCookie("nonce",base64.StdEncoding.EncodeToString(nonce) , 0, "/", "", true, true)
fmt.Println("token:", base64.StdEncoding.EncodeToString(token))
c.HTML(http.StatusOK, "index.html", gin.H{"ping": "pong"})
}
func(pc PubController) MyDec(c *gin.Context) {
var feedback string
var check string
Rec_err := c.PostForm("Rec")
fmt.Println("Rec:", Rec_err)
Rec, err := base64.StdEncoding.DecodeString(Rec_err)
if err != nil {
check = "false"
feedback = "Try again."
SendJsonBack(feedback, check, c)
return
}
Pt_err, err := Myfunc.AESDec(Rec, key, iv)
//
if err != nil || base64.StdEncoding.EncodeToString(Pt_err) == base64.StdEncoding.EncodeToString(sid){
check = "false"
feedback = "Don't try to fool me! Try again."
SendJsonBack(feedback, check, c)
return
}
check = "true"
feedback = "Access Accepted."
Pt := base64.StdEncoding.EncodeToString(Pt_err)
fmt.Println("(DEBUG)Pt: ", Pt)
nonce_hash := Myfunc.Hash(nonce)
pwd = Pt+nonce_hash
fmt.Println("pwd: ",pwd)
SendJsonBack(feedback, check, c)
}
func(pc PubController) CheckPwd(c *gin.Context) {
var feedback string
var check string
Rec := c.PostForm("Password")
if pwd == "" {
check = "false"
feedback = "Give me your token first."
SendJsonBack(feedback, check, c)
return
}
if Rec == pwd {
check = "true"
feedback = "Your flag is: SYC{AL3XEI_FAKE_FLAG}"
} else {
check = "false"
feedback = "Oops! Please try again."
}
SendJsonBack(feedback, check, c)
}my_func.go
查看代码
package Myfunc
import (
"crypto/aes"
"crypto/cipher"
"crypto/rand"
"bytes"
"crypto/sha512"
"encoding/base64"
"fmt"
)
func check(err error) {
if err != nil {
panic(err)
}
}
func GetRandBytes(n int) []byte {
res := make([]byte, n)
_, e := rand.Read(res)
check(e)
return res
}
func Pad(pt []byte) []byte {
padlen := aes.BlockSize - (len(pt) % aes.BlockSize)
padding := bytes.Repeat([]byte{byte(padlen)}, padlen)
return append(pt, padding...)
}
func Unpad(pt []byte) []byte {
padlen := int(pt[len(pt)-1])
return pt[:len(pt)-padlen]
}
func AESEnc(pt []byte, key []byte, iv []byte) ([]byte, error) {
block, e := aes.NewCipher(key)
if e != nil {
return nil, e
}
pt_ := Pad(pt)
fmt.Println("(DEBUG) pt_: ", pt_)
ct := make([]byte, len(pt_))
m := cipher.NewCBCEncrypter(block, iv)
m.CryptBlocks(ct, pt_)
return ct, nil
}
func AESDec(ct []byte, key []byte, iv []byte) ([]byte, error) {
block, e := aes.NewCipher(key)
if e != nil {
return nil, e
}
m := cipher.NewCBCDecrypter(block, iv)
pt_ := make([]byte, len(ct))
m.CryptBlocks(pt_, ct)
return Unpad(pt_), nil
}
func Hash(nonce []byte) string{
h := sha512.New()
h.Write(nonce)
nonce_hash := base64.StdEncoding.EncodeToString(h.Sum(nil))
return nonce_hash
}简单描述一下题目任务,有三个访问接口如下:
func (pc PubController) Router(pr *gin.Engine) {
pr.GET("/", pc.Room)
pr.POST("/api/dec", pc.MyDec)
pr.POST("/api/check", pc.CheckPwd)
}
访问MyDec方法,我们可以用post方式发送一个base64串让服务器解密,服务器正确解密后会检查解密结果是否等于sid,如果不相等则通过检查,并将解密后的结果连接上nonce的sha512值,作为pwd
首先,pwd的后半部分,也就是nonce的sha512值我们是可以获得的,因此主要想的办法是如何去得到pwd的前半部分Pt,也就是MyDec中的AES解密结果。
注意到AES解密后一定会unpad,而myfunc中的pad和unpad是pkcs#7的标准填充方式,而我们利用的点也主要在于unpad函数:
func Unpad(pt []byte) []byte {
padlen := int(pt[len(pt)-1])
return pt[:len(pt)-padlen]
}可以看到它解填充时,只用最后一个字节的值当作填充长度,这对于标准填充过的密文来说,这样解填充当然是没问题的,但是如果不是标准填充过后的密文就会产生问题,这是因为在MyDec中我们可以发送任何base64串,只要他能正确AES解密,并且解密结果不等于sid(也就是token的解密值),服务器就会把解密结果Pt当作pwd的前一部分。
佬还给了两个方法,tql!真的拜了
方法一
也就是说,我们发送任意16字节密文的base64串,服务器应该都能AES解密出16字节明文并解填充,得到最终的Pt。而如果我们可以使解密出的最后一字节值恰为16,那么根据unpad的方式,Pt最终将会是一个空串,所以pwd其实就是nonce的sha512值,所以我们发送nonce的sha512值过去check就能得到flag。
至于如何使解密出的最后一字节值恰为16,我的方法是直接生日攻击就好(。。。),一次有1/256的概率成功,那么爆破256次就有大于50%的概率成功。(惊呆!)
exp:
import requests
from urllib.parse import unquote
from base64 import *
from hashlib import sha512
from Crypto.Util.number import *
from tqdm import *
base_url = "http://47.109.106.62:7842/"
#part1 get nonce
response = requests.get(base_url + "/")
if response.status_code == 200:
cookies = response.cookies
token_cookie = cookies.get("token")
nonce_cookie = cookies.get("nonce")
token = unquote(token_cookie)
nonce = unquote(nonce_cookie)
print("Token:", token)
print("Nonce:", nonce)
nonce_hash = b64encode(sha512(b64decode(nonce)).digest())
#part2 get flag
randombytes = b"0" * 15
for i in trange(256):
#get pwd
temp = randombytes + long_to_bytes(i)
temp = b64encode(temp)
data = {"Rec": temp}
response = requests.post(base_url + "api/dec", data=data)
#get flag
data = {"Password": nonce_hash}
response = requests.post(base_url + "api/check", data=data)
if("Oops!" not in response.text):
print(response.text)
break
#SYC{N0t_S0_E45y_Cryp0W3b}方法二(这个更快,太猛了!)
可以发现刚才的方法是完全没用到token的,而如果用上token,我们则可以完全不爆破。思路就是sid本身是个16字节的值,所以AES加密前会被填充为下面的形式:
sid + b"\x10"*16而又因为是CBC模式加密,所以我们用字节翻转攻击,改变第一组明文的最后一字节,从而实现把最后一个解密出的字节从16改成32,这样解填充的Pt也为空串。
exp:
import requests
from urllib.parse import unquote
from base64 import *
from hashlib import sha512
from Crypto.Util.number import *
base_url = "http://47.109.106.62:7842/"
#part1 get token&nonce
response = requests.get(base_url + "/")
if response.status_code == 200:
cookies = response.cookies
token_cookie = cookies.get("token")
nonce_cookie = cookies.get("nonce")
token = unquote(token_cookie)
nonce = unquote(nonce_cookie)
print("Token:", token)
print("Nonce:", nonce)
nonce_hash = b64encode(sha512(b64decode(nonce)).digest())
#part2 get flag
token1,token2 = b64decode(token)[:16],b64decode(token)[16:]
token1 = token1[:-1] + long_to_bytes((token1[-1] ^ 16 ^ 32))
temp = b64encode(token1+token2)
data = {"Rec": temp}
response = requests.post(base_url + "api/dec", data=data)
#get flag
data = {"Password": nonce_hash}
response = requests.post(base_url + "api/check", data=data)
print(response.text)
#SYC{N0t_S0_E45y_Cryp0W3b}有些题目附件信息太多,没放全。需要Crypto全部完整附件的可以私我!!