NewStarCTF 2023 公开赛道 WEEK1|CRYPTO全解
一、brainfuck
附件信息
++++++++[>>++>++++>++++++>++++++++>++++++++++>++++++++++++>++++++++++++++>++++++++++++++++>++++++++++++++++++>++++++++++++++++++++>++++++++++++++++++++++>++++++++++++++++++++++++>++++++++++++++++++++++++++>++++++++++++++++++++++++++++>++++++++++++++++++++++++++++++<<<<<<<<<<<<<<<<-]>>>>>>>++++++.>----.<-----.>-----.>-----.<<<-.>>++..<.>.++++++.....------.<.>.<<<<<+++.>>>>+.<<<+++++++.>>>+.<<<-------.>>>-.<<<+.+++++++.--..>>>>---.-.<<<<-.+++.>>>>.<<<<-------.+.>>>>>++.在线工具一把梭
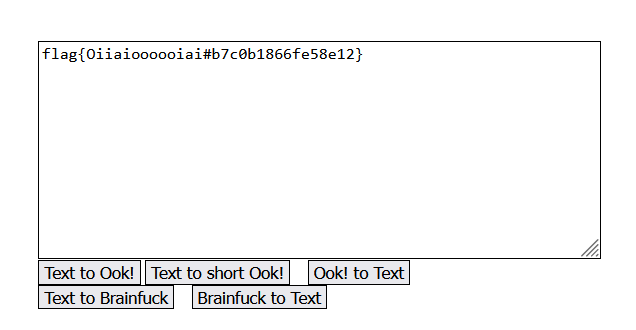
二、Caesar's Secert
题目信息
kqfl{hf3x4w'x_h1umjw_n5_a4wd_3fed}凯撒解码
三、Fence
题目信息
fa{ereigtepanet6680}lgrodrn_h_litx#8fc3栏栅密码
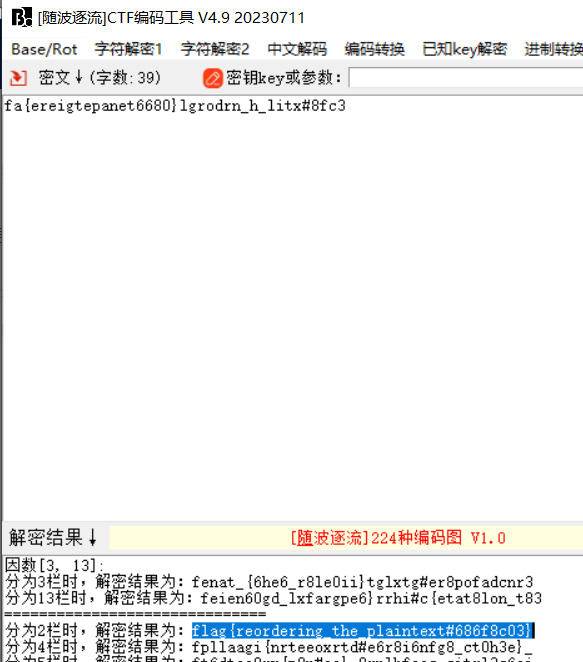
四、Vigenère
题目信息
pqcq{qc_m1kt4_njn_5slp0b_lkyacx_gcdy1ud4_g3nv5x0}维吉尼亚呀呀呀！！根据flag前缀通过偏移量手算key就行，是kfc呀嘿嘿
五、babyencoding
题目信息
part 1 of flag: ZmxhZ3tkYXp6bGluZ19lbmNvZGluZyM0ZTBhZDQ=
part 2 of flag: MYYGGYJQHBSDCZJRMQYGMMJQMMYGGN3BMZSTIMRSMZSWCNY=
part 3 of flag: =8S4U,3DR8SDY,C`S-F5F-C(S,S<R-C`Q9F8S87T`flag分啦三部分，分别来解
part1：base64
part2：base32
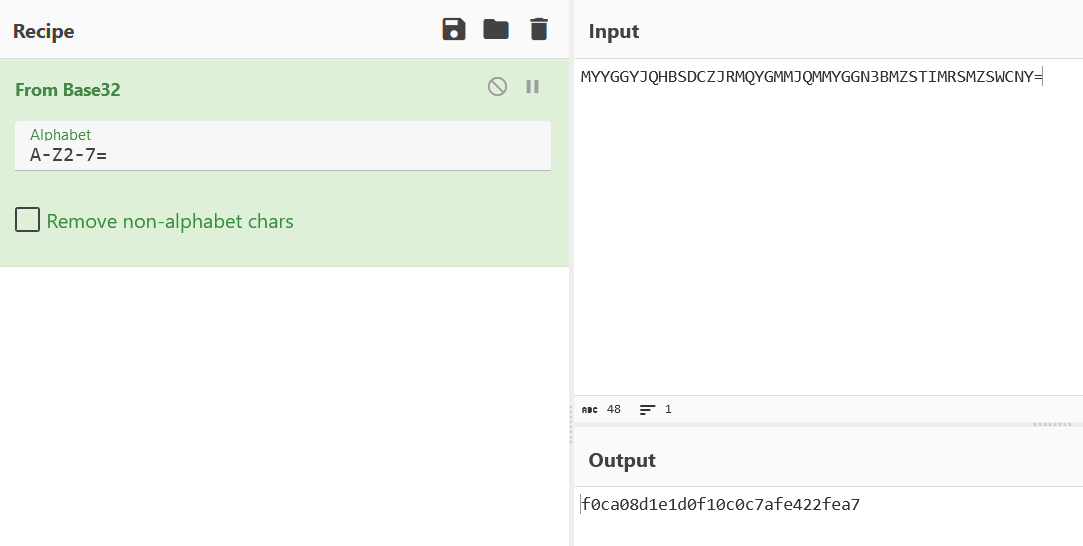
part3：UUencode
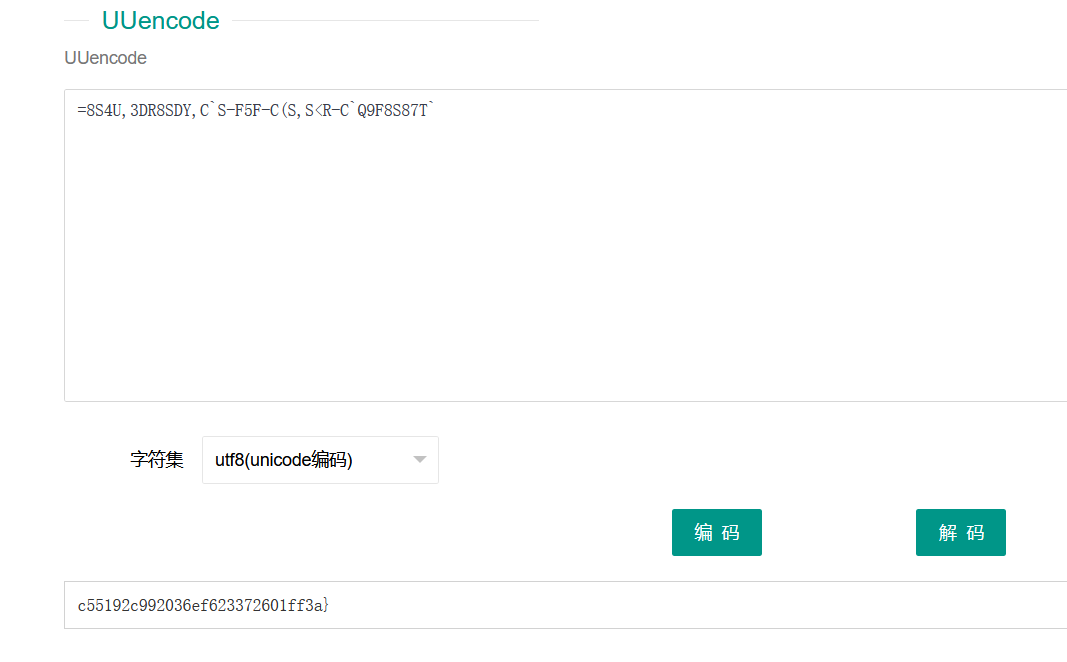
六、babyrsa
题目信息
from Crypto.Util.number import *
from flag import flag
def gen_prime(n):
res = 1
for i in range(15):
res *= getPrime(n)
return res
if __name__ == '__main__':
n = gen_prime(32)
e = 65537
m = bytes_to_long(flag)
c = pow(m,e,n)
print(n)
print(c)
# 17290066070594979571009663381214201320459569851358502368651245514213538229969915658064992558167323586895088933922835353804055772638980251328261
# 14322038433761655404678393568158537849783589481463521075694802654611048898878605144663750410655734675423328256213114422929994037240752995363595脚本：
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 17290066070594979571009663381214201320459569851358502368651245514213538229969915658064992558167323586895088933922835353804055772638980251328261
e = 65537
c = 14322038433761655404678393568158537849783589481463521075694802654611048898878605144663750410655734675423328256213114422929994037240752995363595
p1=2217990919
p2=2338725373
p3=2370292207
p4=2463878387
p5=2706073949
p6=2794985117
p7=2804303069
p8=2923072267
p9=2970591037
p10=3207148519
p11=3654864131
p12=3831680819
p13=3939901243
p14=4093178561
p15=4278428893
phi = (p1 - 1) * (p2 - 1) * (p3 - 1) * (p4 - 1) * (p5 - 1) * (p6 - 1) * (p7 - 1) * (p8 - 1) * (p9 - 1) * (p10 - 1) * (p11 - 1) * (p12 - 1) * (p13 - 1) * (p14 - 1) * (p15 - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#flag{us4_s1ge_t0_cal_phI}七、Small d
题目信息
from secret import flag
from Crypto.Util.number import *
p = getPrime(1024)
q = getPrime(1024)
d = getPrime(32)
e = inverse(d, (p-1)*(q-1))
n = p*q
m = bytes_to_long(flag)
c = pow(m,e,n)
print(c)
print(e)
print(n)
# c = 6755916696778185952300108824880341673727005249517850628424982499865744864158808968764135637141068930913626093598728925195859592078242679206690525678584698906782028671968557701271591419982370839581872779561897896707128815668722609285484978303216863236997021197576337940204757331749701872808443246927772977500576853559531421931943600185923610329322219591977644573509755483679059951426686170296018798771243136530651597181988040668586240449099412301454312937065604961224359235038190145852108473520413909014198600434679037524165523422401364208450631557380207996597981309168360160658308982745545442756884931141501387954248
# e = 8614531087131806536072176126608505396485998912193090420094510792595101158240453985055053653848556325011409922394711124558383619830290017950912353027270400567568622816245822324422993074690183971093882640779808546479195604743230137113293752897968332220989640710311998150108315298333817030634179487075421403617790823560886688860928133117536724977888683732478708628314857313700596522339509581915323452695136877802816003353853220986492007970183551041303875958750496892867954477510966708935358534322867404860267180294538231734184176727805289746004999969923736528783436876728104351783351879340959568183101515294393048651825
# n = 19873634983456087520110552277450497529248494581902299327237268030756398057752510103012336452522030173329321726779935832106030157682672262548076895370443461558851584951681093787821035488952691034250115440441807557595256984719995983158595843451037546929918777883675020571945533922321514120075488490479009468943286990002735169371404973284096869826357659027627815888558391520276866122370551115223282637855894202170474955274129276356625364663165723431215981184996513023372433862053624792195361271141451880123090158644095287045862204954829998614717677163841391272754122687961264723993880239407106030370047794145123292991433识别：e特别大
在RSA中d也称为解密指数，当d比较小的时候，e也就显得特别大了，所以发现e特别大的时候可以考虑低解密指数攻击。
# Sage
def rational_to_contfrac(x, y):
# Converts a rational x/y fraction into a list of partial quotients [a0, ..., an]
a = x // y
pquotients = [a]
while a * y != x:
x, y = y, x - a * y
a = x // y
pquotients.append(a)
return pquotients
def convergents_from_contfrac(frac):
# computes the list of convergents using the list of partial quotients
convs = [];
for i in range(len(frac)): convs.append(contfrac_to_rational(frac[0: i]))
return convs
def contfrac_to_rational(frac):
# Converts a finite continued fraction [a0, ..., an] to an x/y rational.
if len(frac) == 0: return (0, 1)
num = frac[-1]
denom = 1
for _ in range(-2, -len(frac) - 1, -1): num, denom = frac[_] * num + denom, num
return (num, denom)
c = 6755916696778185952300108824880341673727005249517850628424982499865744864158808968764135637141068930913626093598728925195859592078242679206690525678584698906782028671968557701271591419982370839581872779561897896707128815668722609285484978303216863236997021197576337940204757331749701872808443246927772977500576853559531421931943600185923610329322219591977644573509755483679059951426686170296018798771243136530651597181988040668586240449099412301454312937065604961224359235038190145852108473520413909014198600434679037524165523422401364208450631557380207996597981309168360160658308982745545442756884931141501387954248
e = 8614531087131806536072176126608505396485998912193090420094510792595101158240453985055053653848556325011409922394711124558383619830290017950912353027270400567568622816245822324422993074690183971093882640779808546479195604743230137113293752897968332220989640710311998150108315298333817030634179487075421403617790823560886688860928133117536724977888683732478708628314857313700596522339509581915323452695136877802816003353853220986492007970183551041303875958750496892867954477510966708935358534322867404860267180294538231734184176727805289746004999969923736528783436876728104351783351879340959568183101515294393048651825
n = 19873634983456087520110552277450497529248494581902299327237268030756398057752510103012336452522030173329321726779935832106030157682672262548076895370443461558851584951681093787821035488952691034250115440441807557595256984719995983158595843451037546929918777883675020571945533922321514120075488490479009468943286990002735169371404973284096869826357659027627815888558391520276866122370551115223282637855894202170474955274129276356625364663165723431215981184996513023372433862053624792195361271141451880123090158644095287045862204954829998614717677163841391272754122687961264723993880239407106030370047794145123292991433
def egcd(a, b):
if a == 0: return (b, 0, 1)
g, x, y = egcd(b % a, a)
return (g, y - (b // a) * x, x)
def mod_inv(a, m):
g, x, _ = egcd(a, m)
return (x + m) % m
def isqrt(n):
x = n
y = (x + 1) // 2
while y < x:
x = y
y = (x + n // x) // 2
return x
def crack_rsa(e, n):
frac = rational_to_contfrac(e, n)
convergents = convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
# check if x*x - s*x + n = 0 has integer roots
D = s * s - 4 * n
if D >= 0:
sq = isqrt(D)
if sq * sq == D and (s + sq) % 2 == 0: return d
d = crack_rsa(e, n)
m = hex(pow(c, d, n))[2:]
print(bytes.fromhex(m))
#flag{learn_some_continued_fraction_technique#dc16885c}八、babyxor
题目信息
from secret import *
ciphertext = []
for f in flag:
ciphertext.append(f ^ key)
print(bytes(ciphertext).hex())
# e9e3eee8f4f7bffdd0bebad0fcf6e2e2bcfbfdf6d0eee1ebd0eabbf5f6aeaeaeaeaeaef2简单的异或
脚本：
法一：爆破key
a = 'e9e3eee8f4f7bffdd0bebad0fcf6e2e2bcfbfdf6d0eee1ebd0eabbf5f6aeaeaeaeaeaef2'
c = bytes.fromhex(a)
for i in range(256):
flag = []
for j in c:
flag.append(j ^ i)
if b'flag' in bytes(flag):
print(bytes(flag))
# flag{x0r_15_symm3try_and_e4zy!!!!!!}法二：直接求key，key = ord(‘f’) ^ (密文第一个字节)
a = 'e9e3eee8f4f7bffdd0bebad0fcf6e2e2bcfbfdf6d0eee1ebd0eabbf5f6aeaeaeaeaeaef2'
c = bytes.fromhex(a)
key = ord('f') ^ c[0]
flag = []
for j in c:
flag.append(j ^ key)
print(bytes(flag))
# flag{x0r_15_symm3try_and_e4zy!!!!!!}九、Affine
题目信息
from flag import flag, key
modulus = 256
ciphertext = []
for f in flag:
ciphertext.append((key[0]*f + key[1]) % modulus)
print(bytes(ciphertext).hex())
# dd4388ee428bdddd5865cc66aa5887ffcca966109c66edcca920667a88312064题目分析：仿射密码
源码存在两个量 key[0] 和 key[1] 作为密钥a和b
其实仿射密码的本质就是解方程得到a和b
我们可以利用已知明文前缀flag{*****} 获得a和b的值
需要注意一点！！
使用f和l这两个已知字符是无法合适求解的 所以一定要灵活 整体往后取一位用l和a求解就好了
exp：
import gmpy2
#key = '****CENSORED***************' #密钥 censored 被遮盖
flag = 'flag{*******CENSORED********}' #部分明文
data = "dd4388ee428bdddd5865cc66aa5887ffcca966109c66edcca920667a88312064" #密文待解密
encrypted = bytes.fromhex(data)
# encrypted = data
# print(encrypted)
plaindelta = ord(flag[2]) - ord(flag[1])
print(plaindelta)
cipherdalte = encrypted[2] - encrypted[1]
print(cipherdalte)
modulus = 256
a = gmpy2.invert(plaindelta, modulus) * cipherdalte % modulus
b = (encrypted[1] - a * ord(flag[1])) % modulus
print(a,b)
# a = 17
# b = 23
a_inv = gmpy2.invert(a, modulus)
result = ""
for c in encrypted:
result += chr((c - b) * a_inv % modulus)
print(result)
#flag{4ff1ne_c1pher_i5_very_3azy}十、babyaes
题目信息
from Crypto.Cipher import AES
import os
from flag import flag
from Crypto.Util.number import *
def pad(data):
return data + b"".join([b'\x00' for _ in range(0, 16 - len(data))])
def main():
flag_ = pad(flag)
key = os.urandom(16) * 2
iv = os.urandom(16)
print(bytes_to_long(key) ^ bytes_to_long(iv) ^ 1)
aes = AES.new(key, AES.MODE_CBC, iv)
enc_flag = aes.encrypt(flag_)
print(enc_flag)
if __name__ == "__main__":
main()
# 3657491768215750635844958060963805125333761387746954618540958489914964573229
# b'>]\xc1\xe5\x82/\x02\x7ft\xf1B\x8d\n\xc1\x95i'题目分析：
buu上有一道与这道题很类似
key等于字节a的前16位 * 2
iv = 字节a后16位 ^ key的前一半 ^ 1
key,iv都出来了，那么flag就好说了。。
exp:
from Crypto.Util.number import *
from Crypto.Cipher import AES
a = 3657491768215750635844958060963805125333761387746954618540958489914964573229
c = b'>]\xc1\xe5\x82/\x02\x7ft\xf1B\x8d\n\xc1\x95i'
key = long_to_bytes(a)[:16]
iv = bytes_to_long(key) ^ bytes_to_long(long_to_bytes(a)[16:]) ^ 1
aes = AES.new(key * 2,AES.MODE_CBC,long_to_bytes(iv))
flag = aes.decrypt(c)
print(flag)
# flag{firsT_cry_Aes}
