[LitCTF 2023]baby_xor

题目分数：447

题目评分：3.8

题目标签： RSAcoppersmith

题目描述：

- 题目描述:探姬姐姐也很疑惑捏！
- 出题人：3tefanie丶zhouflag以NSSCTF{}形式提交

附件：

附件信息

 from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
assert len(flag)==32
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
c1 = p^m
c2 = pow(m,e,n)
print(f'n = {n}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
"""
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
"""

解题：

1、分析附件c1 = p ^ m，可知想要得到m需要知道p，问题就是p如何得到？

本题考查的是RSA中coppersmith定理，在了解定理后便可入手了。

首先，明文长度已知，p的总长位数pbits=512，因此需要利用c1对p的高位进行爆破，通常取pbits的一半

import gmpy2
from tqdm import *

n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
e=65537
pbits = 512
p_high = c1 >> 256
for i in trange(2**8):
     p4 = p_high<<8
     p4 = p4 + i
     kbits = pbits - p4.nbits()
     p4 = p4 << kbits
     PR.<x> = PolynomialRing(Zmod(n))
     f = x + p4
     roots = f.small_roots(X=2^kbits, beta=0.4, epsilon=0.01)
     if roots:
         p = p4 + int(roots[0])
         break
print(p)

运行结果：

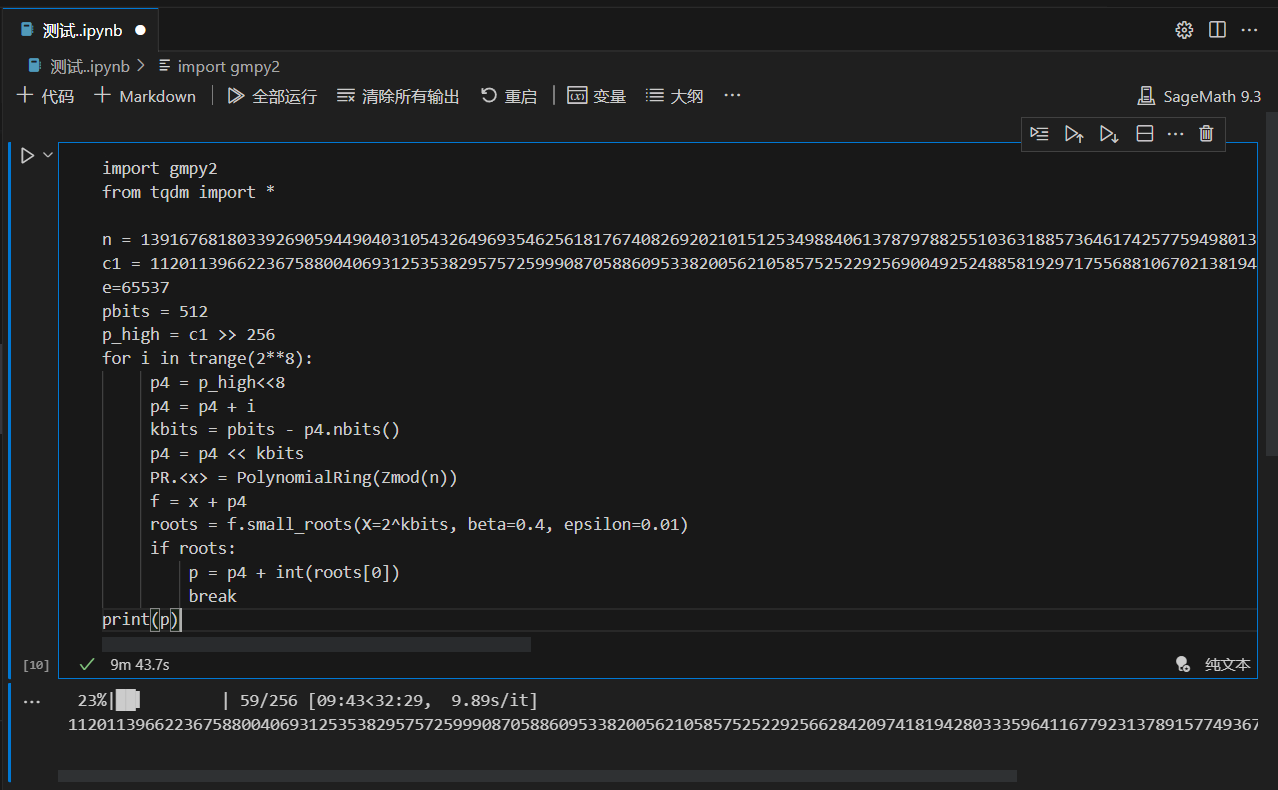
得到：

p = 11201139662236758800406931253538295757259990870588609533820056210585752522925662842097418194280333596411677923137891577493678147771013147838272857867768049

注意：这里我是在VS code里面跑的，需要借助Jupyter来实现，因为pycharm里面有PR.<>的问题有点恶心，不想解决了。使用Jupyter方法可以参考

https://blog.csdn.net/Z987421/article/details/123892074

安装好后，右上角默认是Python处理内核，Python是不行的，需要切换内核，即下图右上角红色圈住部分，至于如何切换内核可以参考

https://zhuanlan.zhihu.com/p/297736314

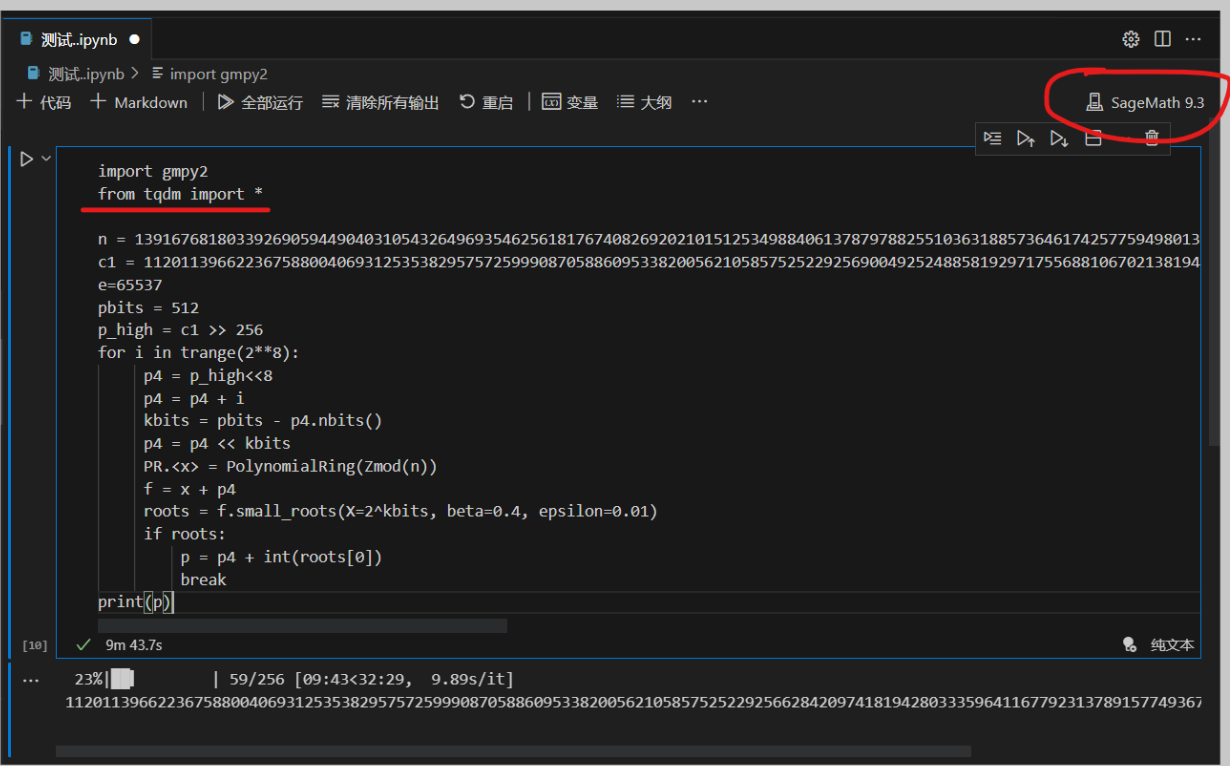
上面操作结束后运行脚本（点击全部运行）会发现有tqdm库报错问题，这个也好解决，点击左上角+代码的地方添加新的代码块，输入! pip install tqdm点击运行便可下载，

注意输入的!是英文状态的，下载完毕即可运行脚本，下面就耐心等待了，也用不了多久，大概到23%左右就得到p了。

2、在上述操作下得到p之后，下面就好解决了，利用c1 = p ^ m直接上代码

import gmpy2
from tqdm import *
from Crypto.Util.number import *

p = 11201139662236758800406931253538295757259990870588609533820056210585752522925662842097418194280333596411677923137891577493678147771013147838272857867768049
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
m = c1 ^ p
flag = long_to_bytes(m)
print(flag)
# LitCTF{oh!!!!coppersmith_is_fun}