[第五空间 2021]ecc
题目分数:366
题目标签: ECCCrypto
题目描述:
你了解椭圆曲线吗附件内容:
chall.sage:
查看代码
print 'Try to solve the 3 ECC'
from secret import flag
from Crypto.Util.number import *
assert(flag[:5]=='flag{')
flag = flag[5:-1]
num1 = bytes_to_long(flag[:7])
num2 = bytes_to_long(flag[7:14])
num3 = bytes_to_long(flag[14:])
def ECC1(num):
p = 146808027458411567
A = 46056180
B = 2316783294673
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num**P
print E
print 'P:',P
print 'Q:',Q
def ECC2(num):
p = 1256438680873352167711863680253958927079458741172412327087203
#import random
#A = random.randrange(389718923781273978681723687163812)
#B = random.randrange(816378675675716537126387613131232121431231)
A = 377999945830334462584412960368612
B = 604811648267717218711247799143415167229480
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num**P
print E
print 'P:',P
print 'Q:',Q
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
print (primes)
dlogs = []
for fac in primes:
t = int(int(P.order()) / int(fac))
dlog = discrete_log(t*Q,t*P,operation="+")
dlogs += [dlog]
print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
print num
print crt(dlogs,primes)
def ECC3(num):
p = 0xd3ceec4c84af8fa5f3e9af91e00cabacaaaecec3da619400e29a25abececfdc9bd678e2708a58acb1bd15370acc39c596807dab6229dca11fd3a217510258d1b
A = 0x95fc77eb3119991a0022168c83eee7178e6c3eeaf75e0fdf1853b8ef4cb97a9058c271ee193b8b27938a07052f918c35eccb027b0b168b4e2566b247b91dc07
B = 0x926b0e42376d112ca971569a8d3b3eda12172dfb4929aea13da7f10fb81f3b96bf1e28b4a396a1fcf38d80b463582e45d06a548e0dc0d567fc668bd119c346b2
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
ECC1(num1)
print '=============='
ECC2(num2)
print '=============='
ECC3(num3)out:
查看代码
Try to solve the 3 ECC
Elliptic Curve defined by y^2 = x^3 + 46056180*x + 2316783294673 over Finite Field of size 146808027458411567
P: (119851377153561800 : 50725039619018388 : 1)
Q: (22306318711744209 : 111808951703508717 : 1)
==============
Elliptic Curve defined by y^2 = x^3 + 377999945830334462584412960368612*x + 604811648267717218711247799143415167229480 over Finite Field of size 1256438680873352167711863680253958927079458741172412327087203
P: (550637390822762334900354060650869238926454800955557622817950 : 700751312208881169841494663466728684704743091638451132521079 : 1)
Q: (1152079922659509908913443110457333432642379532625238229329830 : 819973744403969324837069647827669815566569448190043645544592 : 1)
==============
Elliptic Curve defined by y^2 = x^3 + 490963434153515882934487973185142842357175523008183292296815140698999054658777820556076794490414610737654365807063916602037816955706321036900113929329671*x + 7668542654793784988436499086739239442915170287346121645884096222948338279165302213440060079141960679678526016348025029558335977042712382611197995002316466 over Finite Field of size 11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419
P: (10121571443191913072732572831490534620810835306892634555532657696255506898960536955568544782337611042739846570602400973952350443413585203452769205144937861 : 8425218582467077730409837945083571362745388328043930511865174847436798990397124804357982565055918658197831123970115905304092351218676660067914209199149610 : 1)
Q: (964864009142237137341389653756165935542611153576641370639729304570649749004810980672415306977194223081235401355646820597987366171212332294914445469010927 : 5162185780511783278449342529269970453734248460302908455520831950343371147566682530583160574217543701164101226640565768860451999819324219344705421407572537 : 1)解题:
看到附件有三个椭圆曲线算法,需要解密,下面分别来求
一、椭圆曲线的离散对数问题
看附件:
def ECC1(num):
p = 146808027458411567
A = 46056180
B = 2316783294673
E = EllipticCurve(GF§,[A,B])
P = E.random_point()
Q = numP
print E
print ‘P:’,P
print ‘Q:’,Q
附件输出:
Elliptic Curve defined by y^2 = x^3 + 46056180x + 2316783294673 over Finite Field of size 146808027458411567
P: (119851377153561800 : 50725039619018388 : 1)
Q: (22306318711744209 : 111808951703508717 : 1)
P是椭圆曲线的一个点,Q是椭圆曲线上的另一个点,求num其实就是已知椭圆曲线和两点求私钥,使用sagemath
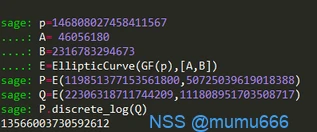
求出flag1=13566003730592612
二、中国剩余定理解决离散对数问题
此算法已在附件给出
factors, exponents = zip(factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
print (primes)
dlogs = []
for fac in primes:
t = int(int(P.order()) / int(fac))
dlog = discrete_log(tQ,t*P,operation=“+”)
dlogs += [dlog]
print("factor: “+str(fac)+”, Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
print num
print (crt(dlogs,primes))
拿到sagemath直接用,如下图:
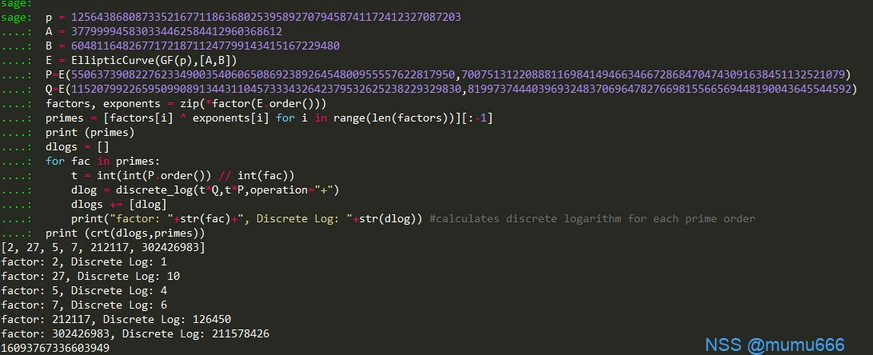
得到flag2=16093767336603949
三、阶数与p相等采用smart’s attack
附件内容:
def ECC3(num):
p = 0xd3ceec4c84af8fa5f3e9af91e00cabacaaaecec3da619400e29a25abececfdc9bd678e2708a58acb1bd15370acc39c596807dab6229dca11fd3a217510258d1b
A = 0x95fc77eb3119991a0022168c83eee7178e6c3eeaf75e0fdf1853b8ef4cb97a9058c271ee193b8b27938a07052f918c35eccb027b0b168b4e2566b247b91dc07
B = 0x926b0e42376d112ca971569a8d3b3eda12172dfb4929aea13da7f10fb81f3b96bf1e28b4a396a1fcf38d80b463582e45d06a548e0dc0d567fc668bd119c346b2
E = EllipticCurve(GF§,[A,B])
P = E.random_point()
Q = num*P
print E
print ‘P:’,P
print ‘Q:’,Q
依然同上面操作,如下图:
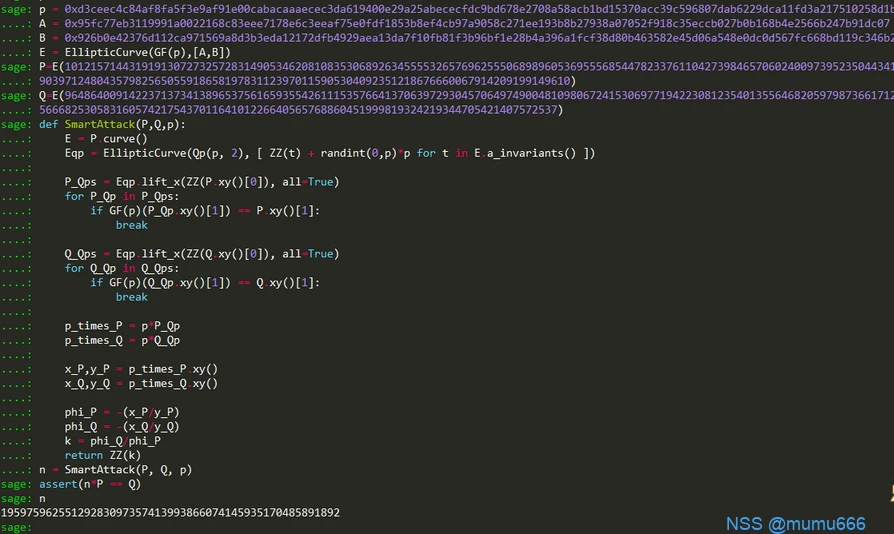
得到flag3=19597596255129283097357413993866074145935170485891892
图中smart’s attack源码如下:
def SmartAttack(P,Q,p):
E = P.curve()
Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])
P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
for P_Qp in P_Qps:
if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
break
Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
for Q_Qp in Q_Qps:
if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
break
p_times_P = p*P_Qp
p_times_Q = p*Q_Qp
x_P,y_P = p_times_P.xy()
x_Q,y_Q = p_times_Q.xy()
phi_P = -(x_P/y_P)
phi_Q = -(x_Q/y_Q)
k = phi_Q/phi_P
return ZZ(k)可以参考网址:https://crypto.stackexchange.com/questions/70454/why-smarts-attack-doesnt-work-on-this-ecdlp
注:上面所述的所有椭圆离散对数问题详解可以参考
https://blog.csdn.net/ckm1607011/article/details/106849551/
四、最后一步
看到附件有:
assert(flag[:5]==‘flag{’)
flag = flag[5:-1]
num1 = bytes_to_long(flag[:7])
num2 = bytes_to_long(flag[7:14])
num3 = bytes_to_long(flag[14:])
于是直接上代码:
from Crypto.Util.number import long_to_bytes
num1=13566003730592612
num2=16093767336603949
num3=19597596255129283097357413993866074145935170485891892
print(long_to_bytes(num1)+long_to_bytes(num2)+long_to_bytes(num3))得到结果:b’025ab3d9-2521-4a81-9957-8c3381622434’
至此本题完美解决,喜欢的小伙伴记得点赞哟!


