自顶向下的归并排序图示解析以及JAVA代码实现

一、归并排序

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

二、算法描述

• 把长度为n的输入序列分成两个长度为n/2的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列。

三、算法图示

1、轨迹图

1). 排序E,M, 排序G,R,
2). 合并在一起.
3). 以此反复.

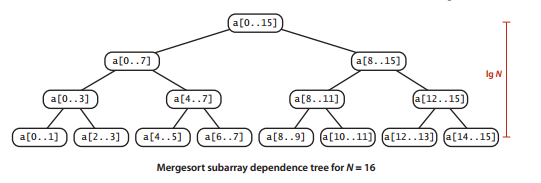
2、依赖书

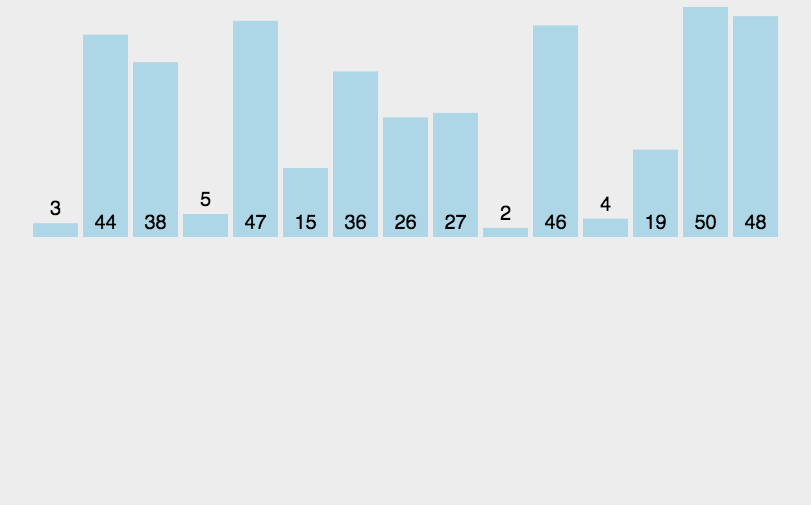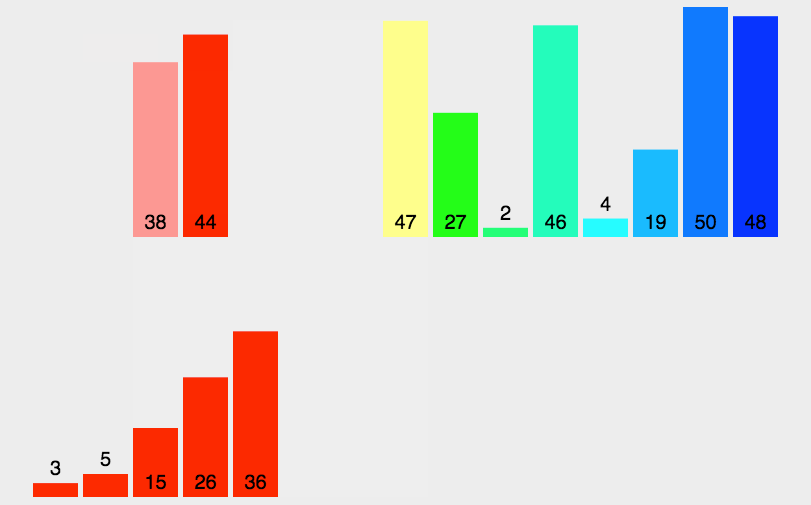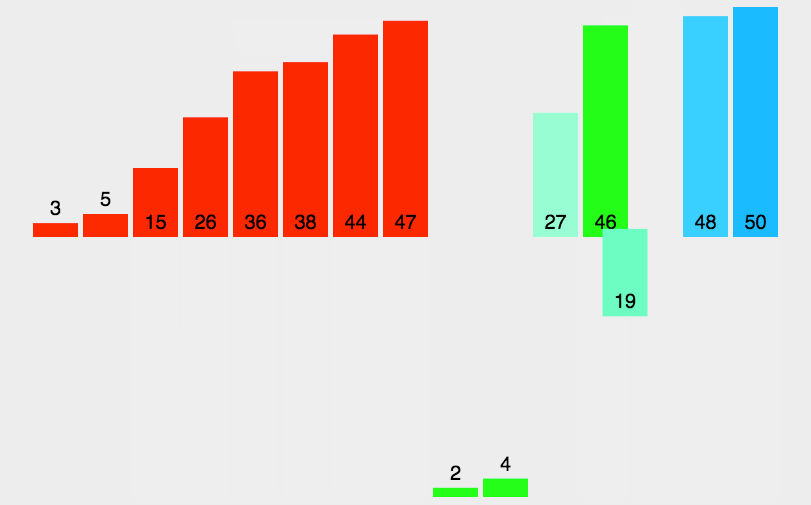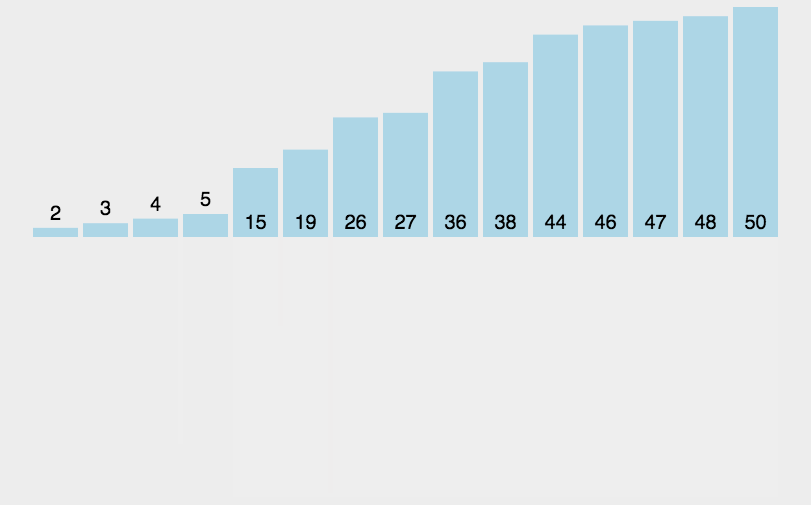
3、动态展示

四、JAVA实现

function mergeSort(arr) {
    varlen = arr.length;
    if(len < 2) {
        returnarr;
    }
    varmiddle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    returnmerge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
    varresult = [];
 
    while(left.length>0 && right.length>0) {
        if(left[0] <= right[0]) {
            result.push(left.shift());
        }else{
            result.push(right.shift());
        }
    }
    while(left.length)
        result.push(left.shift());
    while(right.length)
        result.push(right.shift());
    returnresult;
}

五、复杂度分析

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。