转：Cesium中的相机—WebGL基础

转发：通俗易懂 深入浅出(๑•̀ㅂ•́)و✧

Cesium中的相机—WebGL基础

云上飞47636962 2018-09-24 15:18:58 

分类专栏： STK Cesium

 

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/u011575168/article/details/82824438

版权

Cesium是基于Html5 WebGL技术在浏览器中显示三维物体，本文阐述一下WebGL显示三维物体的基本概念。

需要说明是，在三维场景中，相机(Cesium中为Camera)指的是观察者，即用相机模拟人眼观测，因此在以后各篇章中，为避免读者引起疑惑，以下名词等效：

相机=摄像机=人眼=观察者

WebGL 三维场景渲染原理

WebGL是基于GLSL ES（着色器语言）的，并以字符串的形式在JavaScript中编写的。WebGL中有两种着色器：

• 顶点着色器（Vertex shader）：顶点着色器用来描述顶点特性（如位置、颜色）的程序。
  Vertex（顶点） 是指二维或三维空间中的一个点。
• 片元着色器（Fragment shader）：进行逐片元处理过程（如光照、纹理贴图）的程序。片元(Fragment) 是一个WebGL属于，你可以将其理解为像素（图像的单元）。

简单的说，在三维场景中，仅仅用线条和颜色把图形画出来是远远不够的。你必须考虑，比如，光线照上去之后，或者观察者的视角发生变化，对场景会有些什么影响。着色器可以高度灵活地完成这些工作，提供各种渲染效果。这就是当今计算器制作出的三维场景如此逼真和令人震撼的原因。

当然，在Cesium中，我们不需要接触到底层的东西，Cesium已经全部通过函数的方式为我们包装好相应的功能，使用时直接调用相关API即可。

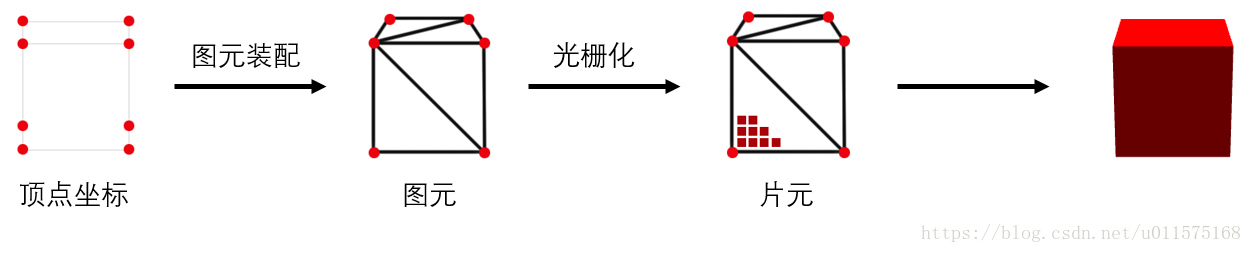
简单的说，任何一个三维模型，都是一系列的点组成，再由点组成一系列的三角形，而在WebGL中也只能通过绘制三种图形（点、线段和三角形）来绘制整个模型。

WebGL绘制过程包括以下三步：

1. 获取顶点坐标
2. 图元装配（即画出一个个三角形）
3. 光栅化（生成片元，即一个个像素点）
   

尽管模型有着成千上万个顶点，但是在渲染过程中，是一个个顶点顺序处理的，也就是说所有顶点的处理步骤是一样的，因此，在各种文档中，阐述坐标转换时，仅仅以一个点为例，读者需要清楚这一点。

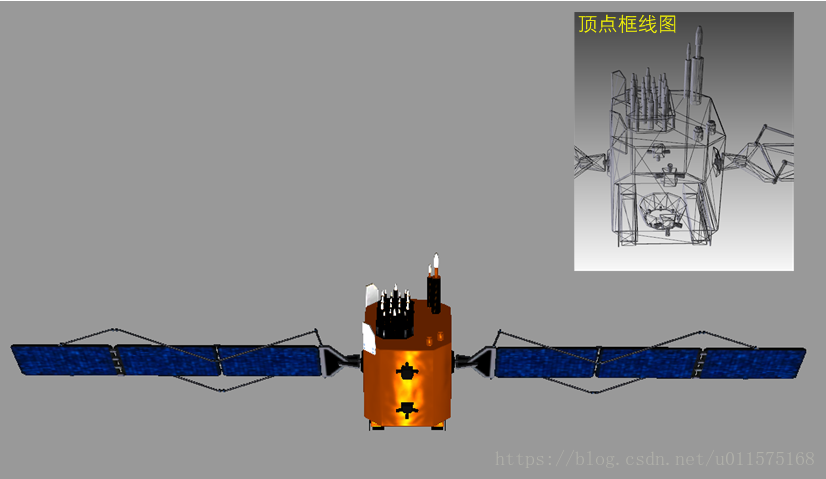
下图为某卫星的渲染图和顶点框线图。

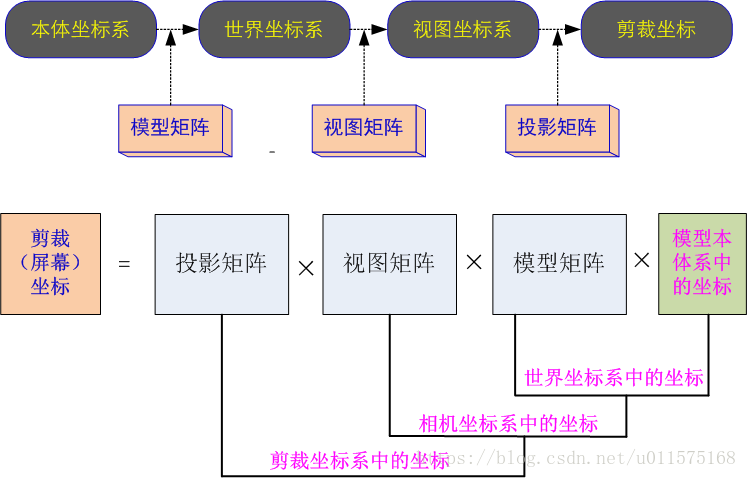
模型矩阵、视图矩阵、投影矩阵

计算机屏幕显示一个三维物体时，实际上是把三维空间中的模型转换为屏幕上的二维的点坐标，本质上是一个投影变换，即：将三维空间中的物体映射到二维屏幕上，基本的流程如下：

1. 在一个世界坐标系中建立场景，场景中所有的对象（即各种三维模型，如地球、飞船、地面站）的顶点坐标均要在世界坐标系中表示。

   但是，通常我们建立模型的时候，模型所有顶点的坐标都是相对模型本体坐标系的，根本不知道世界坐标系，怎么办？
   还有，如果模型一直在运动怎么办？比如卫星绕地球运行。

   没有关系，在WebGL中，缓存中存储的模型顶点的坐标就是原始坐标，通常就是模型本体坐标系下的坐标。在每一帧渲染时，需要根据模型在世界坐标系中的位置和姿态，将模型的所有顶点坐标转换为世界坐标系中的坐标，这个转换过程可用一4×4的矩阵表示，称为模型矩阵(Model Matrix。

2. 有了世界坐标系中的所有顶点坐标还不够，还需要知道相机的位置和观察方位。相机模拟的是人眼对世界的观测，相机的位置不同、方向不同，所观测到的同一个世界的场景也不同，就像我们平时往前看和往后看的景色不一样，但是我们所处的世界都是同一个世界。

   因此，需要根据相机的位置和观察方位，将世界坐标系中的所有顶点坐标转换为视图坐标系 （也称相机坐标系） 中的坐标，这个转换过程也可用一4×4的矩阵表示，称为视图矩阵（View Matrix）

3. 在相机坐标中，所有模型的顶点坐标仍是三维的（具有x,y,z三个分量），而显示器是二维的（x,y两个分量），因此还需将三维的顶点坐标投影到二维平面上去（也称剪裁坐标）。对于人眼观测世界来说，远处的东西显得比近处的小，这种投影方式称之为透视投影，仍可用一4×4的矩阵表示，称为**（透视）投影矩阵（Perspective projection Matrix）**

就是通常所说的模型视图投影矩阵（MVP），流程图见下。

其中，模型矩阵、视图矩阵、投影矩阵均为4×4的矩阵。

Cesium中的世界坐标系与相机坐标系

在Cesium中，Camera对象是处理相机的位置和观察方位的，显然，是属于上述三个矩阵中的视图矩阵。

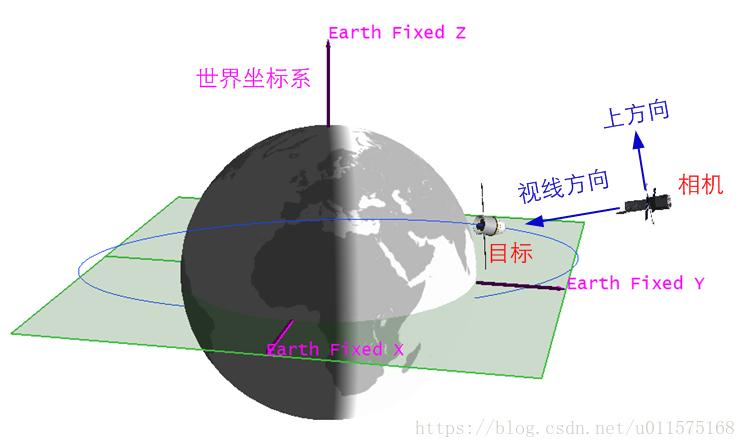
Cesium中，世界坐标系就是地球的WGS84系，也即地球固连坐标系（Earth Fiexed），在此坐标中定义相机的位置与观测方位。

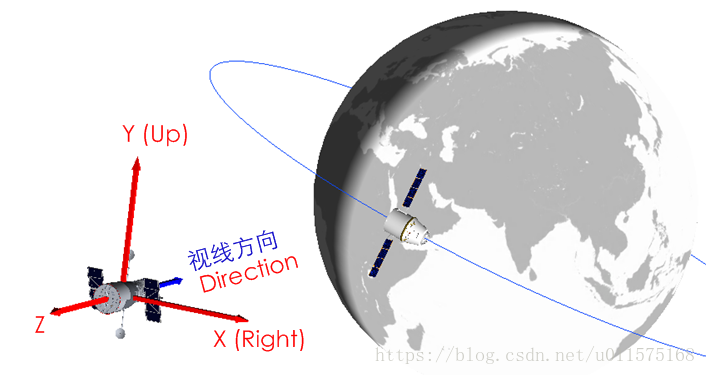
下图中，目标为一运动的飞船，其在WGS84系中的位置是时刻变化的。相机位置、视线方向和相机的上方向均在WGS84系下表达。

根据相机的位置和观察方位，可给出相机观测到的场景，见下示意图。

Cesium中的相机坐标系见下图(使用Hubble望远镜示意相机)，在Camera对象中，通常用三个矢量来表示：Up、Right和Direction，这三个方向确定了相机的观测方位。Up、Right、Direction与相机坐标系（视图坐标系）XYZ三轴的关系为：
X=Right
Y=Up
Z=-Direction

Cesium中，Camera对象中已经包含很多常见设置函数。掌握视图矩阵的概念，即可熟练对Cesium中的相机（Camera）的各项参数进行设置。后续我们会逐渐从源代码分析Camera中各种函数所实现的过程及相应的功能。

综上所述，模型、视图和投影矩阵是三维计算机图形学的基石。关于这三个矩阵的知识虽然不是我们学习Cesium的必须，但是至少能够帮助我们更好地了解那些库函数在做些什么，或者自己直接操作矩阵对象。

参考资料

如果对WebGL基础想具体了解的，可参考以下文章：

• WebGL编程指南
  老外写的一本WebGL入门书籍，从入门到逐渐深入讲解WebGL的各种原理，如果对WebGL原理有兴趣的，强烈推荐。写的浅显易懂，且有代码一步步示范。
• 图解WebGL&Three.js工作原理
• webgl笔记-1.模型视图矩阵和投影矩阵
• webgl开发第一道坎——矩阵与坐标变换