整数、浮点数在计算机中的存储

一、简述

1.1 计算机底层存储数据的基本原理

　　计算机要处理的信息是多种多样的，如数字、文字、符号、图形、音频、视频等，这些信息在人们的眼里是不同的。但对于计算机来说，它们在内存中都是一样的，都是以二进制的形式来表示。要想学习编程，就必须了解二进制，它是计算机处理数据的基础。

　　内存条是一个非常精密的部件，包含了上亿个电子元器件，它们很小，达到了纳米级别。这些元器件，实际上就是电路；电路的电压会变化，要么是 0V，要么是 5V，只有这两种电压。5V 是通电，用1来表示，0V 是断电，用0来表示。所以，一个元器件有2种状态，0 或者 1。我们通过电路来控制这些元器件的通断电，会得到很多0、1的组合。例如，8个元器件有 28=256 种不同的组合，16个元器件有 216=65536 种不同的组合。虽然一个元器件只能表示2个数值，但是多个结合起来就可以表示很多数值了。

　　我们可以给每一种组合赋予特定的含义，例如，可以分别用 1101000、00011100、11111111、00000000、01010101、10101010 来表示 C、语、言、中、文、网 这几个字，那么结合起来 1101000 00011100 11111111 00000000 01010101 10101010 就表示”C语言中文网“。一般情况下我们不一个一个的使用元器件，而是将8个元器件看做一个单位，即使表示很小的数，例如 1，也需要8个，也就是 00000001。1个元器件称为1比特（Bit）或1位，8个元器件称为1字节（Byte），那么16个元器件就是2Byte，32个就是4Byte，以此类推。我们平时使用计算机时，通常只会设计到 KB、MB、GB、TB 这几个单位，PB 和 EB 这两个高级单位一般在大数据处理过程中才会用到。

• 1Byte = 8 Bit
• 1KB = 1024Byte = 2^10Byte
• 1MB = 1024KB = 2^20Byte
• 1GB = 1024MB = 2^30Byte
• 1TB = 1024GB = 2^40Byte
• 1PB = 1024TB = 2^50Byte
• 1EB = 1024PB = 2^60Byte

　　所以，在内存中没有abc这样的字符，也没有gif、jpg这样的图片，只有0和1两个数字，计算机也只认识0和1。所以，计算机使用二进制，而不是我们熟悉的十进制，写入内存中的数据，都会被转换成0和1的组合。

1.2 数据的类型

　　数据的类型有很多，不同的编程语言会将数据的类型分为不同的类别。但是一般的分类是两大类：基本数据类型和引用类型。

• 基本数据类型：直接存储数值。一般有：整型（byte / short / int / long）、浮点型(float / double)、布尔型(boolean)和字符型(char)。
• 引用类型：存储的是地址，数组、字符串、结构体、对象等

二、整数的存储

2.1 整数的基本概念

　　大家知道，整数包括负数，零，和正数。计算机中的整数分为有符号数和无符号数。

• 有符号数：最高位表示符号，即最高位为0，表示正数，最高位为1，表示负数。如果用N位来表示整数，那么有符号数的范围为：[-2^(N-1)，(2^(N-1))-1]。用8位来表示有符号整数数，由于第8位用于表示了符号，因此，整数的表示范围为[-128，+127]。
• 无符号数：表示非负数，整个位数都用来表示整数的值。如果用N位来表示整数，无符号数的表示范围为[0，(2^N)-1]。用8位来表示有符号整数数，则无符号数的表示范围为[0，255]。

2.2 整数的编码方式

　　整数的编码分为原码、反码、和补码。计算里使用的是补码的存储方式。它们的定义如下：

• 原码：在数值前面增加了一位符号位（即最高位为符号位），该位为0表示正数，该位为1表示负数，其余位表示数值的大小。
• 反码：正数的反码与其原码相同。负数的反码是对其原码逐位取反，但符号位除外。
• 补码：正数的补码与其原码相同，负数的补码就是对该负数的反码加1。

　　因为计算机是以补码来存储整数的，所以补码就显得很重要。那么如何计算整数的补码呢？下面以具体例子来说明。 

100   的补码：01100100 
0      的补码：0 
-100 的补码：绝对值：01100100 -->取反加1：10011011+1 -->10011100 
1      的补码：00000001 
-1    的补码：绝对值：00000001 -->取反加1：111111110+1 -->11111111 
127   的补码：01111111 
-128 的补码：绝对值：10000000 -->取反加1：01111111+1 -->10000000 在计算机系统中，数值一律用补码来表示（存储）。 

　　从定义可以看出，正数的补码，反码，原码相同。0的补码就是本身。那么负数的原码和补码如何转换呢？已知一个负数求补码方法：绝对值原码按位求反加1。已知负数补码求负数方法：符号位不变，其他位按位求反加1。对于8位整数来说，补码的表示范围为[-128，127]。 大家应该记住一些常见的补码的表示，这些数包括但不局限于下面表中列出的数：

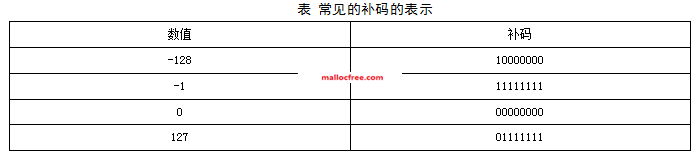
　　那么有了原码，计算机为什么还要用补码呢？

　　来看看它们的运算情况。 假设字长为8位 ，那么原码的运算方式为： 1 - 1 = 1 + ( -1 ) =(00000001) + (10000001) = (10000010) = -2 ，这显然不正确。原码在两个整数的加法运算中是没有问题的，问题出现在带符号位的负数身上。 原码无法满足运算要求，因此对除符号位外的其余各位逐位取反就产生了反码。反码的取值空间和原码相同且一一对应。下面是反码的减法运算： 1 - 1 = 1 + ( -1 )= (00000001) + (11111110) = (11111111) = ( -0 )  没问题。 1 – 2 = 1 + ( -2 ) = (00000001) + (11111101) = (11111110) = ( -1 )  正确。反码的问题出现在(+0)和(-0)上，因为在人们的计算概念中零是没有正负之分的。 再来看补码的加减运算如下： 1 - 1 = 1 + （-1） = (00000001) + (11111111) = (00000000) = 0 正确。 1 – 2 = 1 + （-2） = (00000001) + (11111110) = (11111111) = ( -1 )  正确。

　　通过补码的运算，可以看出补码的设计目的是： 

• 使符号位能与有效值部分一起参加运算，从而简化运算规则。
• 使减法运算转换为加法运算，进一步简化计算机中运算器的线路设计。 
• 此外，在补码中用-128代替了-0，所以没有+0和-0之分，符合常理，所以补码的表示范围为： -128~0~127共256个。

　　注意：-128没有相对应的原码和反码，-128的补码为：10000000。 

三、浮点数的存储

　　一般的编程语言都是将浮点类型的数据采用单精度类型（ float）和双精度类型(double)来存储，float 数据占用 32bit，double 数据占用 64bit，我们在声明一个变量  float f= 2.25f;  的时候，是如何分配内存的呢？如果胡乱分配，那世界岂不是乱套了么，其实不论是 float 还是 double 在存储方式上都是遵从 IEEE 的规范的， float 遵从的是 IEEE R32.24 ,而 double 遵从的是 R64.53。无论是单精度还是双精度在存储中都分为三个部分：

• 浮点数表示的数值：V = (-1)^s × M × 2^E
• 符号(sign) ：1个bit表示，当s=0，V为正数；当s=1，V为负数。
• 阶码(exponent) ：E的作用是对浮点数加权，用于存储科学计数法中的指数数据，并且采用移位存储。float类型的阶码是 8 bits，double类型的阶码是 11 bits。
• 尾数(significand) ：M是一个二进制小数，因为是二进制，所以科学计数法中这个值范围是：1≤M<2。(和十进制中范围为1~10一样)

　　R32.24 和 R64.53 的存储方式都是用科学计数法来存储数据的。比如 8.25 用十进制的科学计数法表示就为:8.25*10^1 ,而 120.5 可以表示为:1.205*10^2 ,这些小学的知识就不用多说了吧。而我们的傻蛋计算机根本不认识十进制的数据，他只认识 0， 1，所以在计算机存储中，首先要将上面的数更改为二进制的科学计数法表示， 8.25 用二进制表示可表示为 1000.01,大家不会连这都不会转换吧?那我估计要没辙了。 120.5 用二进制表示为：1110110.1 用二进制的科学计数法表示 1000.01 可以表示为 1.0001* 2^3,1110110.1可以表示为 1.1101101* 2^6。

　　IEEE 754对有效数字M和指数E，还有一些特别规定。前面说过，1≤M<2，也就是说，M可以写成1.xxxxxx的形式，其中xxxxxx表示小数部分。IEEE 754规定，在计算机内部保存 M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位float浮点数为例，留给M只有23位，将第一位的1舍去以后，等于可以保存24位有效数字。 道理就是在这里，那 24bit 能精确到小数点后几位呢，我们知道 9 的二进制表示为 1001，所以 4bit 能精确十进制中的 1 位小数点， 24bit 就能使 float 能精确到小数点后 6 位。  

　　至于指数E，情况就比较复杂。 首先，E为一个无符号整数（unsigned int）这意味着，如果E为8位 (float类型) ，它的取值范围为0~255；如果E为11位（double类型），它的取值范围  为0~2047。但是，我们知道，科学计数法中的E是可以出现负数的（因为0.75用科学计数法表示就是1.1*2^-1），所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

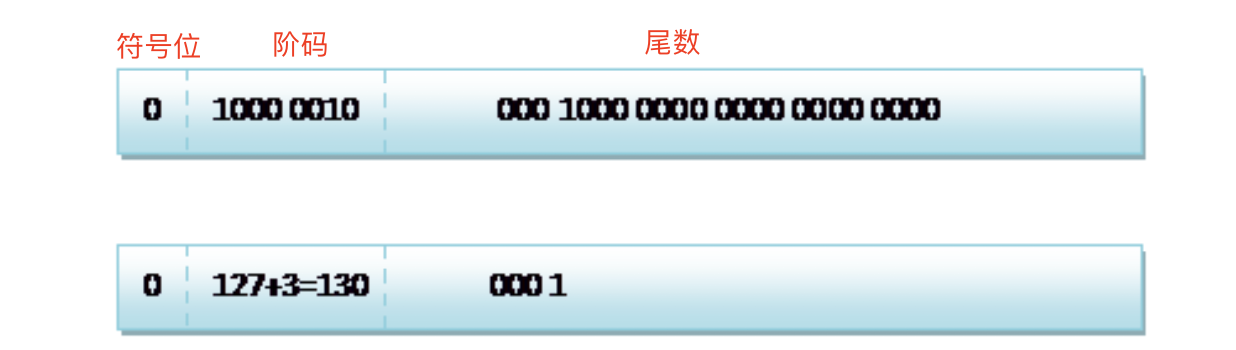
　　接下来我们看下 8.25用float类型存储的数据到底是什么样的？8.25f用二进制的科学计数法表示为:1.0001*2^3，按照上面的存储方式，符号位s = 0，表示为正；指数位 E = 3+127=130 ,尾数部分为1.0001，去掉最前面的整数1，就是M = 0001，所以8.25f用float类型在内存中存储的格式就是：