分治法 —— 最大子序和

原题：53. 最大子序和 (leetcode-cn.com)

题解：https://blog.csdn.net/weixin_44686373/article/details/107619930

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

分治法就是把一个很复杂的问题划分成各个小的问题去解决，针对这道题，要想找最大子串和，看下图

 

 

 

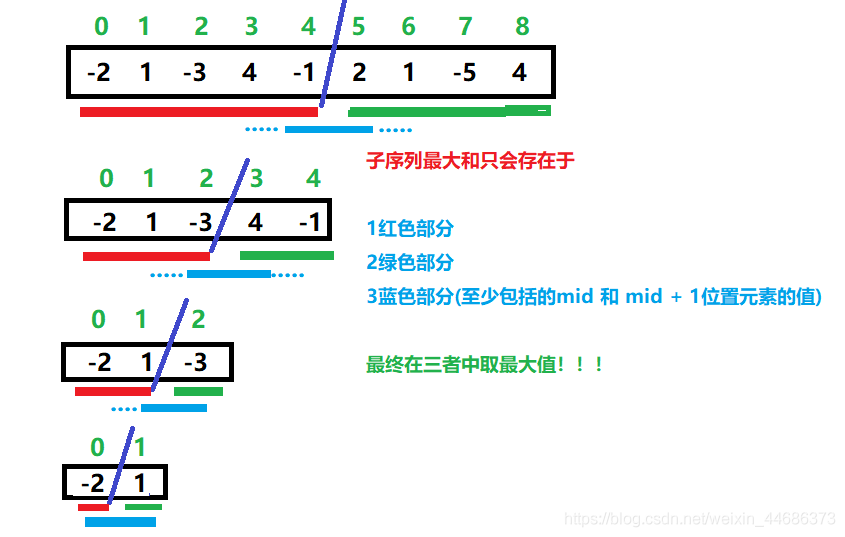
最大值产生于红色部分， 绿色部分以及蓝色部分三者之间

如何求红色，绿色，蓝色三个part各自的最大值呢?

看图可知，每一个颜色的part都可以分解小规模问题。例如图中的红色part再可以分为红，绿，蓝三个part， 接着继续分继续分继续分 直到红色part和绿色part仅有一个元素时停止

大规模问题转化为小规模问题，最后每个小规模问题解合并即是大规模问题解
即是分治策略

代码：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        return maxSub(nums,0,nums.size()-1);
    }

    int maxSub(vector<int>& nums,int left,int right){
        if(left == right) return nums[left];//当只有一个元素的时候

        int mid = ( left + right ) / 2;//从中间分成两部分；

        int leftmax = maxSub(nums,left,mid);//计算左边子串最大和
        int rightmax = maxSub(nums,mid+1,right);//计算右边子串最大和

        //计算中间的子串和
        int left_midmax = INT_MIN;//先算左边最大（包含mid）
        int left_midsum = 0;
        for(int i = mid;i >= left; i--){
            left_midsum+=nums[i];
            if(left_midsum > left_midmax) left_midmax = left_midsum;
        }
        int right_midmax = INT_MIN;//右边最大（包含mid + 1 ）
        int right_midsum = 0;
        for(int i = mid+1;i <=right; i++){
            right_midsum+=nums[i];
            if(right_midsum > right_midmax) right_midmax = right_midsum;
        }
        int midmax = right_midmax+left_midmax;

        return max(max(leftmax,rightmax),midmax);
    }
};

在计算中间子串和的时候做一个小小的改变：

//计算中间的子串和
        int midmax = INT_MIN;
        int midsum = 0;
        for(int i = mid;i >= left; i--){
            midsum+=nums[i];
            if(midsum > midmax) midmax = midsum;
        }
        if(midmax!=INT_MIN)midsum = midmax;
        for(int i = mid+1;i <=right; i++){
            midsum+=nums[i];
            if(midsum > midmax) midmax = midsum;
        }