127. 单词接龙 哈希表 BFS 优化建图 双向搜索

127. 单词接龙

题解出处：https://leetcode-cn.com/problems/word-ladder/solution/dan-ci-jie-long-by-leetcode-solution/

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

1. 每次转换只能改变一个字母。
2. 转换过程中的中间单词必须是字典中的单词。

说明:

• 如果不存在这样的转换序列，返回 0。
• 所有单词具有相同的长度。
• 所有单词只由小写字母组成。
• 字典中不存在重复的单词。
• 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

 

 

方法一：广度优先搜索 + 优化建图

思路

本题要求的是最短转换序列的长度，看到最短首先想到的就是广度优先搜索。想到广度优先搜索自然而然的就能想到图，但是本题并没有直截了当的给出图的模型，因此我们需要把它抽象成图的模型。

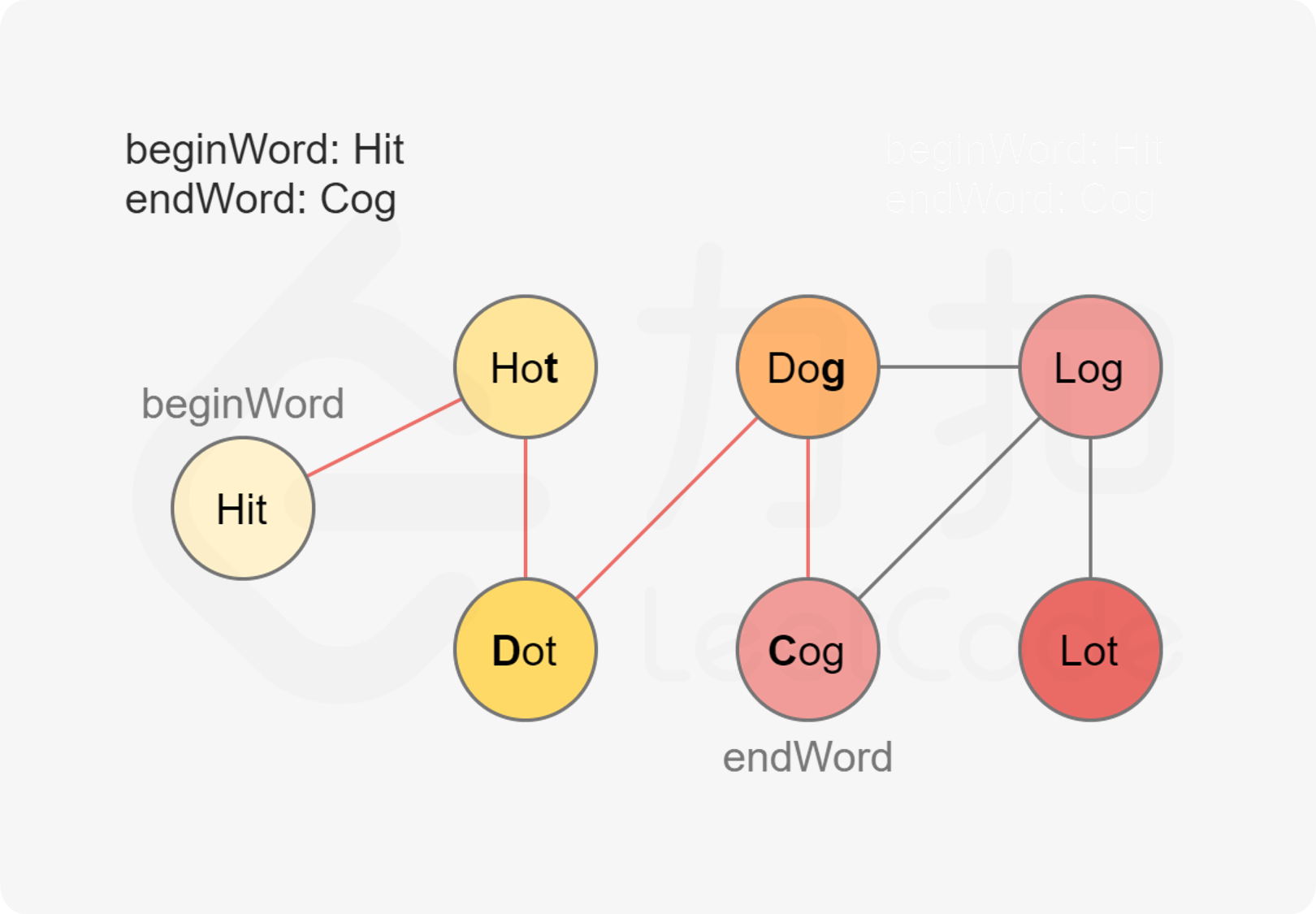
我们可以把每个单词都抽象为一个点，如果两个单词可以只改变一个字母进行转换，那么说明他们之间有一条双向边。因此我们只需要把满足转换条件的点相连，就形成了一张图。

基于该图，我们以 beginWord 为图的起点，以 endWord 为终点进行广度优先搜索，寻找 beginWord 到 endWord 的最短路径。

 

算法

基于上面的思路我们考虑如何编程实现。

首先为了方便表示，我们先给每一个单词标号，即给每个单词分配一个 id。创建一个由单词 word 到 id 对应的映射 wordId，并将 beginWord 与 wordList 中所有的单词都加入这个映射中。之后我们检查 endWord 是否在该映射内，若不存在，则输入无解。我们可以使用哈希表实现上面的映射关系。

然后我们需要建图，依据朴素的思路，我们可以枚举每一对单词的组合，判断它们是否恰好相差一个字符，以判断这两个单词对应的节点是否能够相连。但是这样效率太低，我们可以优化建图。

具体地，我们可以创建虚拟节点。对于单词 hit，我们创建三个虚拟节点 *it、h*t、hi*，并让 hit 向这三个虚拟节点分别连一条边即可。如果一个单词能够转化为 hit，那么该单词必然会连接到这三个虚拟节点之一。对于每一个单词，我们枚举它连接到的虚拟节点，把该单词对应的 id 与这些虚拟节点对应的 id 相连即可。

最后我们将起点加入队列开始广度优先搜索，当搜索到终点时，我们就找到了最短路径的长度。注意因为添加了虚拟节点，所以我们得到的距离为实际最短路径长度的两倍。同时我们并未计算起点对答案的贡献，所以我们应当返回距离的一半再加一的结果。

class Solution {
public:
    vector<vector<int>> edge;//边
    unordered_map<string,int> words;//结点
    int num = 0;

    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        int end = inwordlist(endWord,wordList) ;
        if( end == wordList.size()) return 0;
        wordList.push_back(beginWord);
        for(int i = 0 ; i < wordList.size(); i++){
            createline(wordList[i]);
        }
        vector<int> dis(num, INT_MAX);//距离
        queue<int> find;
        find.push(words[beginWord]);
        dis[words[beginWord]] = 0;

        while(!find.empty()){
            int now = find.front();
            for(int i = 0; i <edge[now].size();i++){
                if(dis[edge[now][i]]== INT_MAX){
                    dis[edge[now][i]] =  dis[now] +1; 
                    find.push(edge[now][i]);
                }
                if(edge[now][i] == words[endWord]) {
                     return dis[words[endWord]]/2+1;
                } 
                
            }
            find.pop();
        }
        return 0;
       
        
        
        
    }
    void createword(string A){
        if (!words.count(A)) {
             words[A] = num;
             num++;
             edge.emplace_back();
        }
        
    }
    void createline(string A){
        createword(A);
        int K = words[A];
        for(char& t : A){
            char tmp = t;
            t = '*';
            createword(A);
            edge[K].push_back(words[A]);
            edge[words[A]].push_back(K);
            t = tmp;
        }
    }

    int inwordlist(string endWord, vector<string>& wordList){
        for(int i = 0; i<wordList.size();i++){
            if(endWord == wordList[i]) return i;
        }
        return wordList.size();
    }
};

 

 

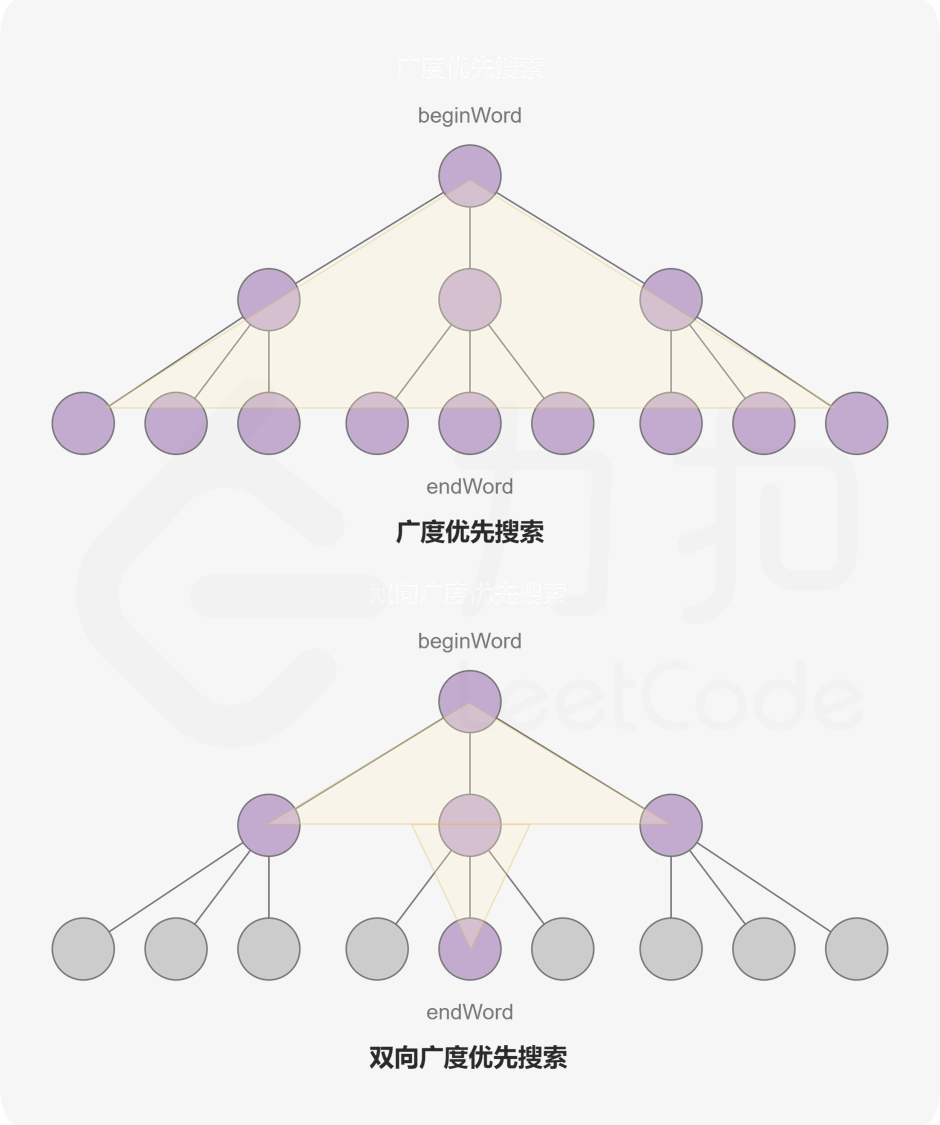
根据给定字典构造的图可能会很大，而广度优先搜索的搜索空间大小依赖于每层节点的分支数量。假如每个节点的分支数量相同，搜索空间会随着层数的增长指数级的增加。考虑一个简单的二叉树，每一层都是满二叉树的扩展，节点的数量会以 2 为底数呈指数增长。

如果使用两个同时进行的广搜可以有效地减少搜索空间。一边从 beginWord 开始，另一边从 endWord 开始。我们每次从两边各扩展一层节点，当发现某一时刻两边都访问过同一顶点时就停止搜索。这就是双向广度优先搜索，它可以可观地减少搜索空间大小，从而提高代码运行效率。