面试题 02.08. 环路检测 快慢指针
给定一个链表,如果它是有环链表,实现一个算法返回环路的开头节点。
有环链表的定义:在链表中某个节点的next元素指向在它前面出现过的节点,则表明该链表存在环路。

示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。
方法:快慢指针
概念:快慢指针是指移动的步长,即每次向前移动速度的快慢。(例如,让快指针每次沿链表向前移动2,慢指针每次向前移动1)
1. 判断存不存在环路:当快指针到达NULL的时候,说明不存在环路。遍历就可以。
2. 找到环入口:
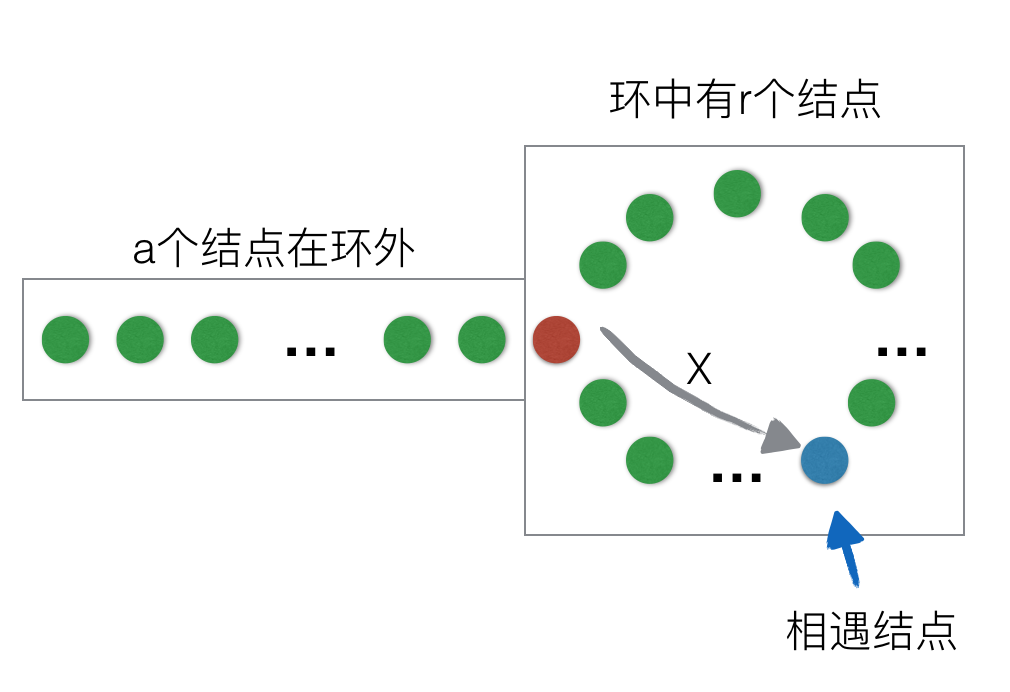
假设从头结点开始,有a个结点在环外,环中有r个结点。快指针和慢指针都从头指针出发,快指针每次走 2 步,慢指针每次走 1 步,在经过一段时间以后,在环中相遇,距离环入口的距离是 X。
此时,慢指针走过的路程为 a+X;
如果 a 较大的话,快指针可能现在已经在环中走过几圈了,假设快指针从入环开始已经走过 k(k>=1) 个整圈,则快指针走过的路程为 a+X+k*r;
快指针走过的路程是慢指针的 2 倍,所以 2*(a+X) = a+X+k*r,即 a = k*r - X = (k-1)*r + r - X;
观察一下,r-X 正好是相遇结点到环入口的距离 ,也就是说,如果现在让慢指针从头结点出发,快指针从相遇结点出发,每次步长均为 1,它们会在环入口相遇。
代码:
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 ListNode *detectCycle(ListNode *head) { 12 ListNode* pro;//快指针 13 ListNode* last;//慢指针 14 pro = head; 15 last = head; 16 if(!head) return head; 17 do{ 18 if(!pro->next) return pro->next; 19 pro = pro->next; 20 last = last->next; 21 if(!pro->next) return pro->next; 22 pro = pro->next; 23 }while(pro != last); 24 25 last = head; 26 while(pro != last){ 27 pro = pro->next; 28 last = last->next; 29 } 30 31 return last; 32 } 33 };
快慢指针的其他应用:
1. 在有序链表中寻找中位数。原理:快指针移动速度是慢指针移动速度的两倍。所以快指针到达链表尾时,慢指针到达中点。(需要判断链表节点奇偶数)如果快指针移动x步到达表尾则为奇数。若为倒数第二个节点则为偶数(可根据规则返回上中位或下中位或上下一半);
2. 两个单向链表判断他们是否相交
思路:首先用快慢指针判断是否有环
1)如果都没有环,如果两个单链表有公共结点,则两个单链表从某个结点开始,他们的next指向同一结点。(由于是单链表结点,每一结点只有一个next,所以从第一个公共结点开始,他们所有结点都是重合的)。既若两个单链表的末尾结点相同则相交。寻找第一个相交结点的方法:
a.在其中一个单链表上顺序遍历每个结点,每遍历一个结点,在另外一个链表上顺序遍历每个结点。
b.首先两个链表各遍历一次求表长l1,l2,两链表差为l.然后现在长的链表上遍历L,然后同步遍历,第一个相同的结点就是公共结点。时间复杂度(O(m+n))
2)如果一个存在环,另外一个不存在环则不可能相交。
3)如果利用快慢指针发现两单链表都存在环,则判断一个链表上快慢指针相遇的那个结点是否在另一个链表上。如果在则相交,否在不相交。如果相交,两个链表的入口点可能不是环上同一结点,利用上边的方法分别找出各自的入口点,可以定义任意一个入口点为相交的第一个结点。


