英文社区优文转载和翻译：Fewshot Learning 2篇

Advances in few-shot learning: a guided tour

现在，few-shot learning 是一个激动人心的机器学习领域。深度神经网络从大量数据集中提取复杂统计数据和学习高级特征的能力已得到证实。然而，目前的深度学习方法与人类感知形成鲜明对比的是样本效率低下 - 甚至一个孩子在看到一张照片后也能识别长颈鹿。微调预先训练的模型是实现高样本效率的流行策略，但它是一种事后黑客攻击。机器学习可以做得更好。few-shot learning 旨在解决这些问题。在本文中，我将通过深入研究三篇前沿论文，探讨一些近期的学习方法。

1. 匹配网络：可微分的最近邻分类器原型网络。

2. 学习原型：表示模型

3. 不可知的元学习：学习微调

我将从对n-shot，k-way分类任务的简要解释开始，这些任务是少数镜头学习的事实基准。我在单个Github存储库中复制了这些论文的主要结果。

The n-shot, k-way task

算法执行小镜头学习的能力通常通过其在n-shot，k-way任务上的性能来测量。这些运行如下：

1. 模型被赋予一个属于一个新的，以前看不见的类的查询样本。

2. 它还被赋予一个支持集S，由n个示例组成，每个示例来自k个不同的看不见的类。

3. 然后算法必须确定查询样本中属于哪个支持集类。

Matching Networks

                   

虽然之前有很多关于深度学习的少数几种方法的研究，但匹配网络是第一个对n-shot，k-way任务进行训练和测试的人。这种吸引力很简单 - 对相同任务的培训和评估使我们能够以端到端的方式优化目标任务。诸如连体网络的早期方法使用成对验证丢失来执行度量学习，然后在单独的阶段中使用学习的度量空间来执行最近邻居分类。这不是最佳的，因为初始嵌入功能被训练以最大化在不同任务上的性能。但是，匹配网络将嵌入和分类相结合，形成端到端的可区分最近邻分类器。匹配网络首先将高维样本嵌入低维空间，然后执行下面等式描述的最近邻分类的广义形式。

                        

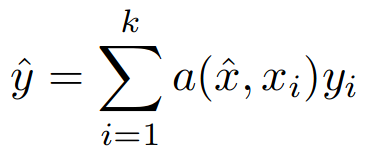
这意味着模型的预测y ^是支持集的标签y_i的加权和，其中权重是查询之间的成对相似度函数a（x ^，x_i）。例如，x ^和支持集样本x_i。该等式中的标记y_i是单热编码标签向量。请注意，如果我们选择a（x ^，x_i）为查询样本的最近k个样本为1 / k，则为0，否则我们恢复k近邻算法。需要注意的关键是匹配网络端到端可区分，前提是注意函数a（x ^，x_i）是可微分的。作者在嵌入空间中选择直接的softmax与余弦相似性，因为它们的注意函数为a（x，x_i）。他们用于几次拍摄图像分类问题的嵌入功能是CNN，当然，它是可区分的，因此使得注意力和匹配网络完全可区分。这意味着可以直接使用典型方法（如随机梯度下降）对整个模型进行端到端拟合。

             

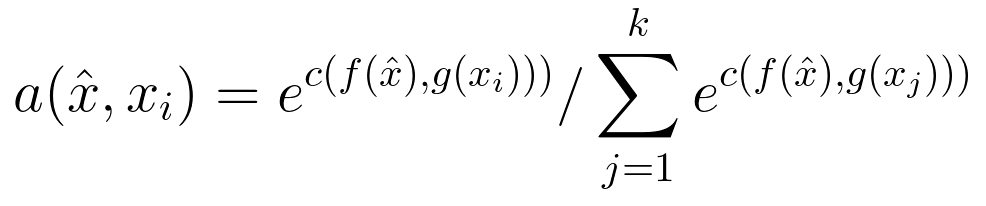
在上面的等式中，c表示余弦相似度，函数f和g分别是查询和支持集样本的嵌入函数。该等式的另一种解释是支持集是一种形式的存储器，并且在看到新样本时，网络通过从该存储器检索具有相似内容的样本的标签来生成预测。有趣的是，支持集和查询集嵌入函数f和g不同的可能性保持开放，以便为模型提供更大的灵活性。事实上，Vinyals等人正是这样做的，并简要介绍了完整上下文嵌入或FCE的概念。他们认为嵌入函数的近视性质是一个弱点，因为支持集x_i的每个元素都以g（x_i）的形式嵌入，其方式独立于支持集的其余部分和查询样本。他们提出嵌入函数f（x ^）和g（x_i）应采用更一般的形式f（x ^，S）和g（x_i，S），其中S是支持集。这背后的原因是，如果两个支持集项目非常接近，例如我们在狗品种之间进行细粒度分类，我们应该改变样本嵌入的方式以增加这些样本的可区分性。在实践中，作者使用LSTM来计算支持的FCE，然后使用另一个LSTM来注意修改查询样本的嵌入。这导致了明显的性能提升，代价是引入了更多的计算和支持集的稍微不吸引人的任意排序。总而言之，这是一篇非常新颖的论文，它提出了完全可微分的神经邻居算法的概念。

Prototypical Networks

                                       

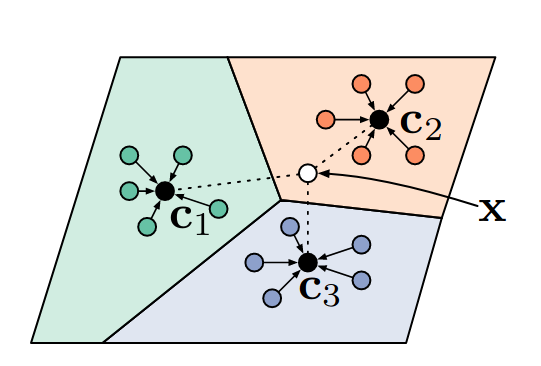
在Prototypical Networks中，Snell等人以类原型的形式应用了引人注目的归纳偏差，以实现令人印象深刻的几次性能 - 超出匹配网络而没有FCE的复杂性。关键的假设是存在嵌入，其中来自每个类聚类的样本围绕单个原型表示，其仅仅是单个样本的均值。在n> 1的情况下，该想法简化了n-shot分类，因为通过获取最接近的类原型的标签简单地执行分类。

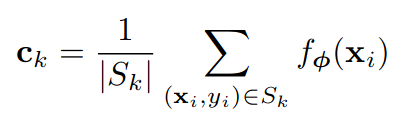
S_k是属于类k的支持集，f_φ是嵌入函数。本文的另一个贡献是在度量学习中使用欧氏距离超过余弦距离的有说服力的理论论证，这也证明了使用类均值作为原型表示的合理性。关键是要认识到平方欧氏距离（但不是余弦距离）是一类特定距离函数的成员，称为Bregman散度。考虑聚类问题，即找到一组点的质心，使得质心和所有其他点之间的总距离最小化。已经证明，如果你的距离函数是一个Bregman散度（例如欧氏距离平方），那么满足这个条件的质心就是群集的平均值 - 然而这不是余弦距离的情况。当将一组点表示为单个点时，该质心是最小化信息丢失的点。这种直觉得到了实验的支持，因为作者发现ProtoNets和他们自己的匹配网络实现都是通过从余弦到欧氏距离的交换来全面改进的。原型网络也适用于零射击学习，人们可以直接从类的高级描述中学习类原型，例如标记属性或自然语言描述。完成此操作后，可以将新图像分类为特定类，而无需查看该类的图像。在他们的实验中，他们仅根据颜色，形状和羽毛图案等属性对鸟类图像进行零射击物种分类。我非常喜欢这篇论文，因为它在本文所有方法的典型基准测试中取得了最高的性能，同时也是优雅的，也是我最容易重现的。干得好Snell等人。

Model-agnostic Meta-learning (MAML)

Finn等人通过学习可以快速适应新任务的网络初始化，采用一种非常不同的方法来进行少数学习 - 这是一种元学习或学习学习的形式。这种元学习的最终结果是一个模型，只需一步的常规梯度下降就可以在新任务上达到高性能。这种方法的优点在于它不仅可以用于监督回归和分类问题，还可以用于使用任何可微分模型的强化学习。

                                   

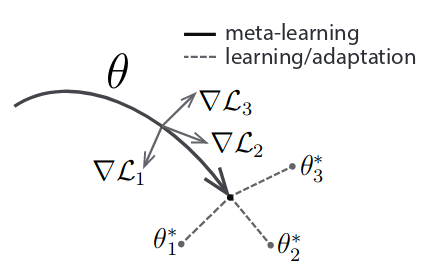
θ 代表元学习者的权重。梯度L是任务的损失，我在元批中，并且星号θi是每个任务的最佳权重。MAML不会像大多数深度学习算法那样学习批量样本，而是批量完成AKA元批量任务。对于元批处理中的每个任务，我们首先使用基础元学习器的权重初始化新的“快速模型”。然后，我们计算梯度并因此从该任务中抽取的样本更新参数并更新快速模型的权重，例如对快速模型的权重执行典型的小批量随机梯度下降。

                  

在参数更新之后，我们从同一任务中抽取一些看不见的样本，并计算元学习器的更新权重（AKA快速模型）任务的损失。最后一步是通过从更新后权重中获取损失总和的梯度来更新元学习者的权重。这实际上是采用梯度的梯度，因此是二阶更新 -  MAML算法通过展开的训练过程进行区分。

                

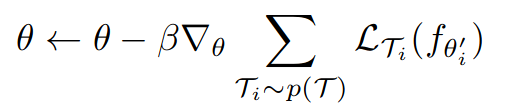
                         元学习者的权值更新。Beta是学习率超参数，p（T）是任务的分布。

这是关键步骤，因为这意味着我们在梯度步骤之后优化基本模型的性能，例如我们正在优化快速简便的梯度下降。这样的结果是元学习器可以通过梯度下降来训练，数据集小到每个类的单个例子而没有过度拟合。来自OpenAI的后续文章提供了一些有价值的直觉，说明为什么使用梯度更新的泰勒扩展。他们得出的结论是，MAML不仅最大限度地减少了任务分配的预期损失，而且最大化了来自同一任务的梯度更新之间的预期内积。因此，它正在优化批次之间的泛化。

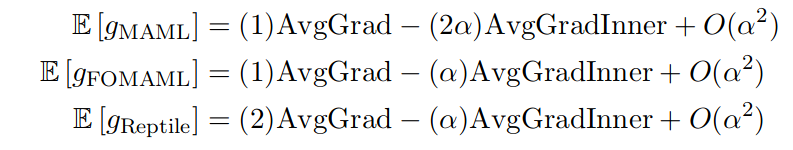
上述方程组显示了MAML梯度的期望，MAMMAL（FORMAL）的一阶简化和Reptile，这是同一篇论文中介绍的一阶元学习算法。AvgGrad术语表示任务丢失，AvgGradInner术语表示泛化术语。请注意，对于学习速率alpha中的前导顺序，所有算法都执行非常类似的更新，其中二阶MAML将最高权重放在泛化项上。也许MAMMAL的唯一缺点是二阶更新，因为计算损失的二阶导数是非常大的内存和计算密集型。然而，诸如FORMAL和Reptile之类的一阶简化产生非常相似的性能，暗示二阶更新可以用更新的权重上的梯度近似。然而，高计算要求与模型不可知元学习是一篇精彩的论文无关，这一论文为机器学习开辟了令人兴奋的新途径。

总结

few-shot learning 的领域正在快速发展，虽然还有很多东西需要学习，但我相信这个领域的研究人员将继续缩小机器和人类表现之间的差距，以应对极少数学习的挑战性任务。我希望你喜欢阅读这篇文章。

Advances in few-shot learning: reproducing results in PyTorch

 

 

（To be continued ...）

 

参考资料：

1. Advances in few-shot learning: a guided tour

2. Advances in few-shot learning: reproducing results in PyTorch