英文社区优文转载和翻译：A Look at Gradient Descent and RMSprop Optimizers

Introduction

我们可以调整无数的超参数来提高神经网络的性能。但是，并非所有这些都会显着影响网络的性能。可以使算法收敛或爆炸之间的差异的一个参数是我们选择的优化器。我们可以选择相当多的优化器，让我们来看看两个最广泛使用的优化器。

渐变下降优化器

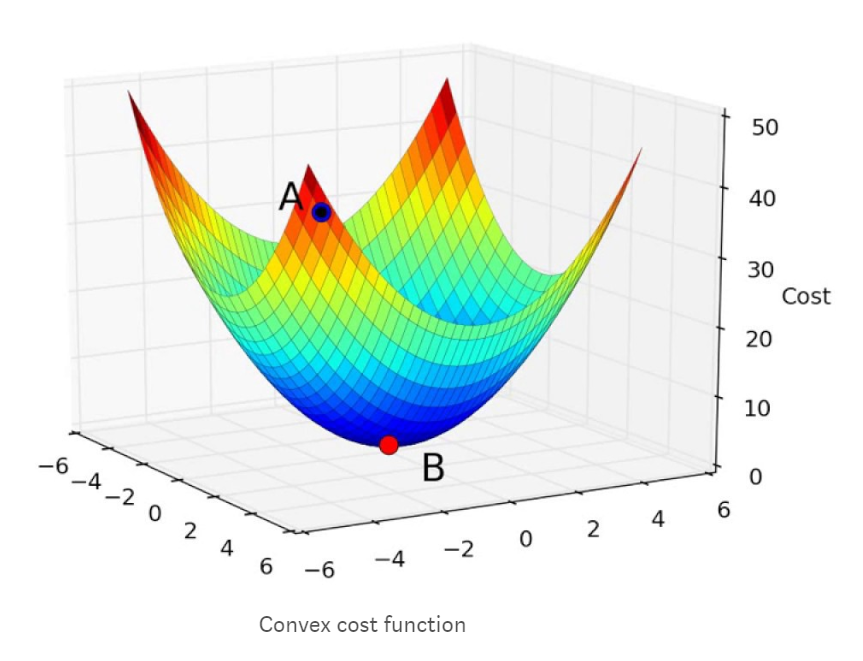
梯度下降可能是所有优化器中最受欢迎和广泛使用的。找到神经网络的最佳值是一种简单有效的方法。所有优化器的目标是达到成本函数达到最小值的全局最小值。如果您尝试以三维方式显示成本函数，则会显示如下所示的图形。

                                        

随机梯度下降

　　 - 算法对于数据中的每个例子

　　 - 找到神经网络预测的值

　　 - 计算损失函数的损失　

　　 - 找到损失函数的偏导数，这些偏导数产生梯度

　　 - 使用梯度更新权值和bias

 

每当我们找到梯度并更新权重和偏差的值时，我们就会越接近最佳值。在我们开始训练神经网络之前，我们的成本会很高，由上图中显示的A点表示。通过训练神经网络的每次迭代（找到梯度并更新权重和偏差），成本降低并且更接近全局最小值，其由上图中的点B表示。下面的模拟将为我们迭代训练模型时如何达到全局最小值提供更好的直观理解。

                              

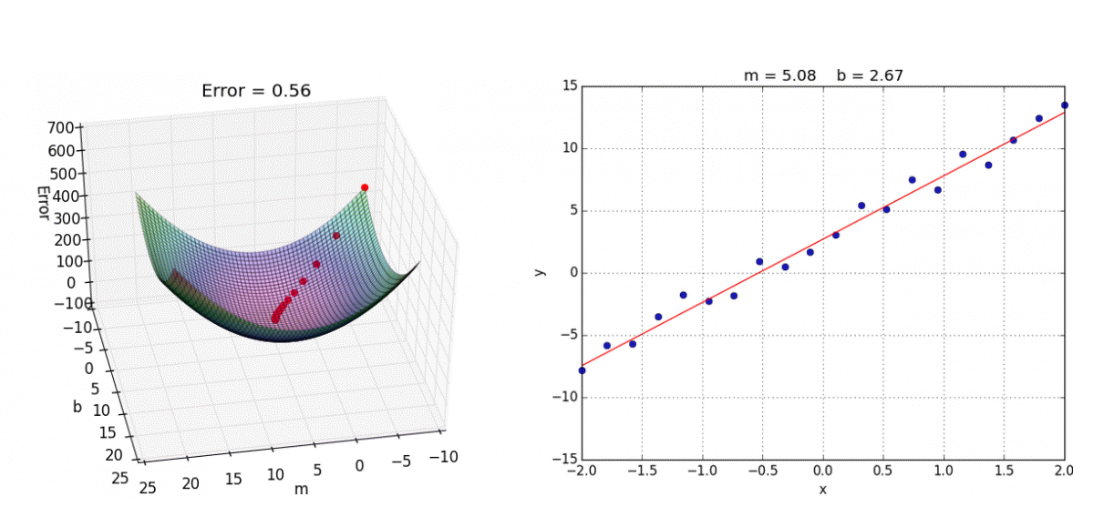
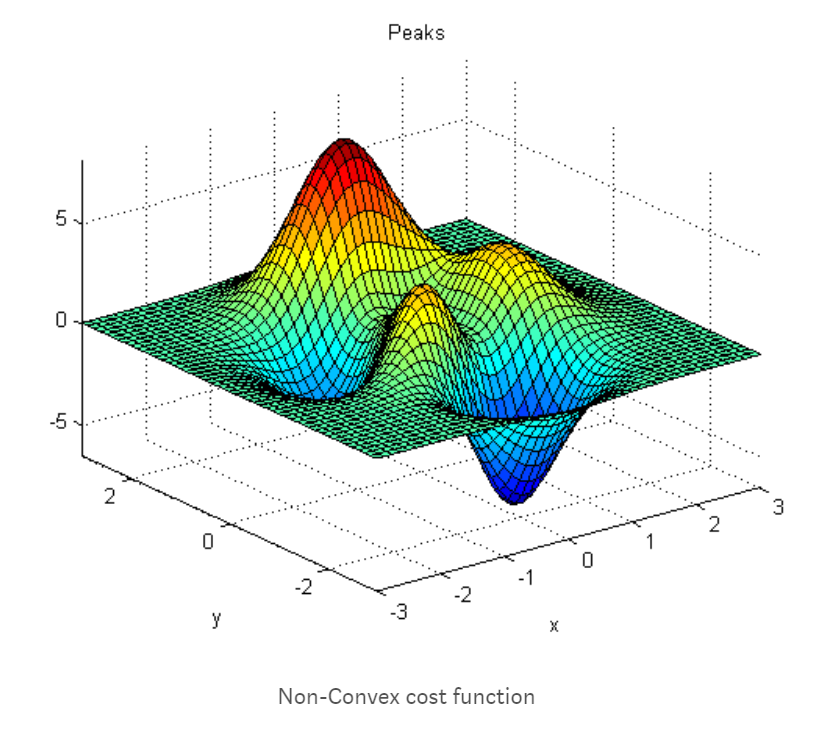
我们的成本函数并不总是如上图所示那样平滑。很多时候，这些成本函数都是非凸的。非凸函数的问题在于，您可能会陷入局部最小值，并且您的损失可能永远不会收敛到全局最小值。看看下面的图片。从上图中可以看出，图中有两个最小值，两个中只有一个是全局最小值。我们的神经网络有可能错过全局最小值并收敛到局部最小值。有一些方法可以限制网络融合，例如。我们可以改变学习率或使用动力等。

                                   

 

学习率

                                    

学习率可能是梯度下降的最重要方面，也可能是其他优化者。让我借鉴一个类比来更好地解释学习率。想象一下作为一个坑的成本函数，你将从顶部开始，你的目标是到达坑的底部。您可以将学习率视为您将要达到底部（全局最小值）的步骤。如果您选择较大的值作为学习率，您将对权重和偏差值进行重大更改，即。你将会大幅跳跃到底部。您也有可能超过全局最小值（底部）并最终位于坑的另一侧而不是底部。学习率很高，你永远无法收敛到全球最低点，并且总会在全球最低点附近徘徊。如果你选择一个较小的值作为学习率，你会失去超过最小值的风险，但你的算法会有更长的时间收敛，例如，你采取较短的步骤，但你必须采取更多的步骤。因此，你需要训练更长的时间。此外，如果成本函数是非凸的，那么您的算法可能很容易被困在局部最小值中，并且它将无法退出并收敛到全局最小值。学习率没有通用的正确值。它归结为实验和直觉。

                               

具有动量的梯度下降（Gradient Descent with Momentum）

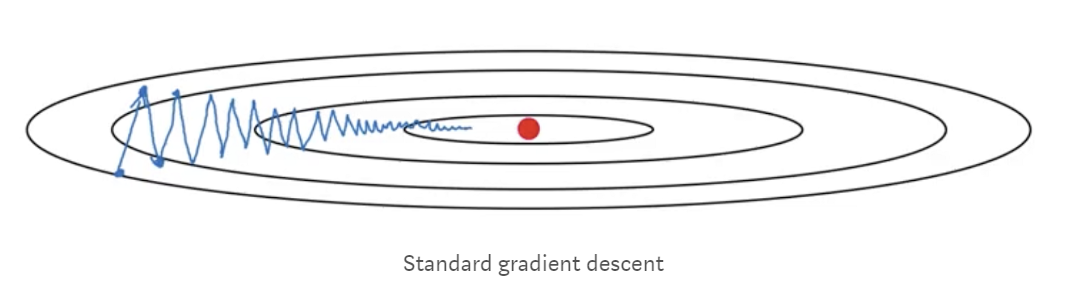
几乎总是这样，具有动量的梯度下降比标准梯度下降算法收敛得更快。在标准梯度下降算法中，您将在一个方向上采取更大的步骤而在另一个方向上采取更小的步骤，这会减慢算法的速度。在下图所示的图像中，您可以看到标准梯度下降在y方向上占据较大的台阶，在x方向上占据较小的台阶。如果我们的算法能够减少在y方向上采取的步骤并且将步骤的方向集中在x方向上，则我们的算法将更快地收敛。这就是动量，它限制了一个方向的振荡，使我们的算法可以更快地收敛。此外，由于限制了在y方向上采取的步数，我们可以设置更高的学习率。

RMSprop Optimizer

RMSprop优化器类似于具有动量的梯度下降算法。RMSprop优化器限制垂直方向的振荡。因此，我们可以提高我们的学习率，我们的算法可以在水平方向上采取更大的步骤，更快地收敛。RMSprop和梯度下降之间的差异在于如何计算梯度。以下等式显示如何计算RMSprop和梯度下降与动量的梯度。动量值用β表示，通常设为0.9。如果您对优化器背后的数学不感兴趣，可以跳过以下等式。

           

 

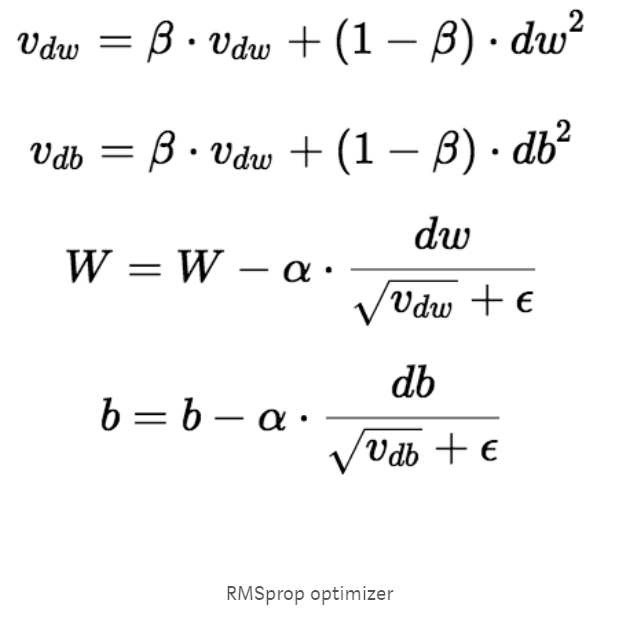
有时V_dw的值可能非常接近0。然后，我们的权重值可能会爆炸。为防止梯度爆炸，我们在分母中包含一个参数 ε，该参数设置为一个较小的值。

总结

优化器是神经网络的重要组成部分，了解它们的工作原理将帮助您选择用于您的应用程序的神经网络。我希望这篇文章有助于做出这个决定。