从逆序对发展
其实逆序对不仅仅是可以用
1、离散化+权值线段树
2、动态开点+权值线段树
如果您还没有看到这两个解法,不要着急,下面是链接:从逆序对开始
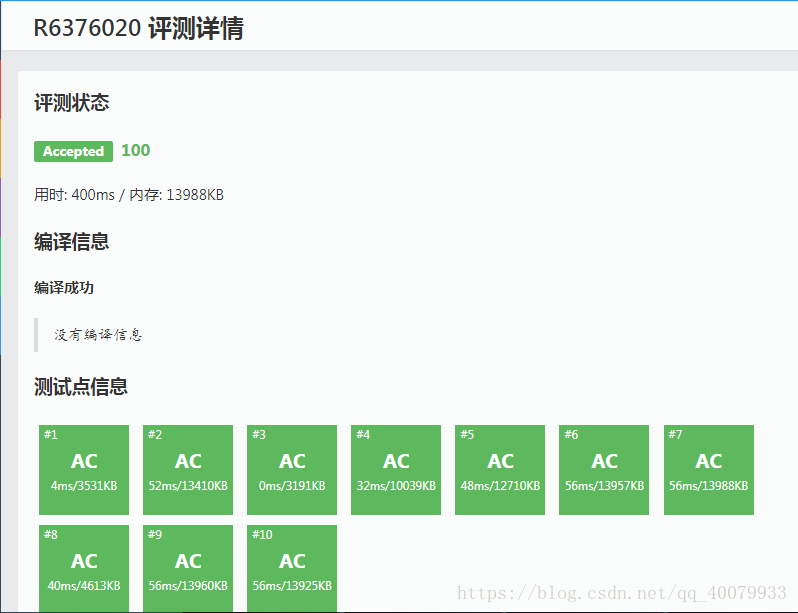
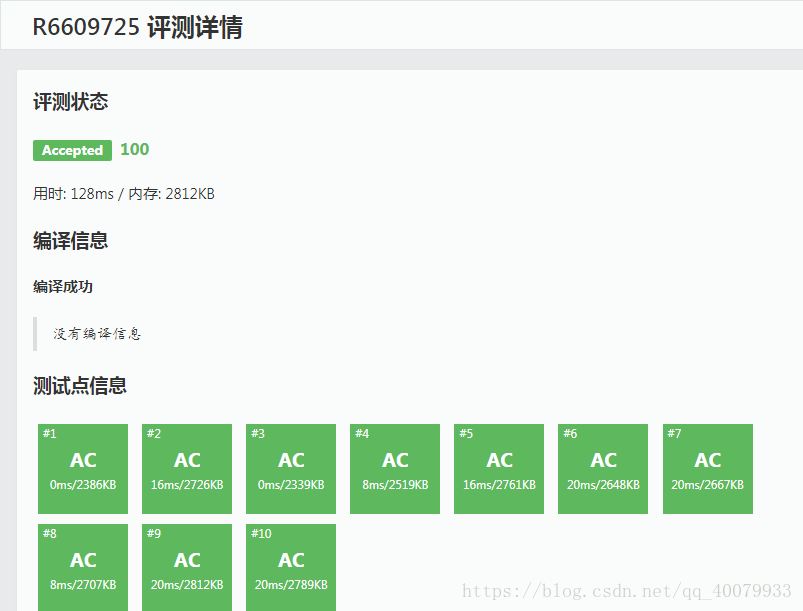
这道题已经被我淡忘一周了,可是他的灵魂我一直没有忘记,直到昨天,有一个同学提醒我这道题能不能用树状数组做,我一下子就惊醒了,我发现这个东西应该是一个非常好的点子,因为树状数组本来就要比线段树快并且空间比线段树小,最重要的是,这玩意儿还非常的好写,所以今天早上我成功的用树状数组AC了这道题,结果非常理想下面上几张图:
下面是线段树跑出的结果:
下面是树状数组跑出的结果:
没有学过树状数组吗?戳这里☞树状数组
大家只要认真学习了以后并且认真看了前面链接博客的离散化的操作那么我相信这道题很快就可以脑补出来!
代码如下:(很短的!!!)
#include<bits/stdc++.h>
using namespace std;
const int N=40005;
struct sd{
int loc,val;
}a[N];
int n;
int maxx=0;
int x[N],o[N],ans=0;
int lowbit(int a){return a&-a;}
void modify(int num)
{
while(num<=maxx)
{
o[num]+=1;
num+=lowbit(num);
}
}
int query(int num)
{
int an=0;
while(num)
{
an+=o[num];num-=lowbit(num);
}
return an;
}
bool cmp(sd a,sd b){
if(a.val<b.val)
return true;
return false;
}
void lisanhua(int n)
{
for(int i=1;i<=n;++i){
cin>>a[i].val;
a[i].loc=i;
}
sort(a+1,a+1+n,cmp);
int cnt=1;
for(int i=1;i<=n;++i){
if(i==1||a[i].val==a[i-1].val)
x[a[i].loc]=cnt;
else{
cnt++;
x[a[i].loc]=cnt;
}
}
}
int main()
{
std::ios::sync_with_stdio(false);cin>>n;
lisanhua(n);
for(int i=1;i<=n;++i) if(maxx<x[i]) maxx=x[i];
memset(o,0,sizeof(o));
for(int i=1;i<=n;++i){
modify(maxx+1-x[i]);
ans+=query(maxx-x[i]);
}
cout<<ans;
return 0;
}好了第一种算法讲完了,下面我们来讲一讲万能解法Splay(伸展树)
还是一样的节奏,不会Splay的戳这里☞Splay详解
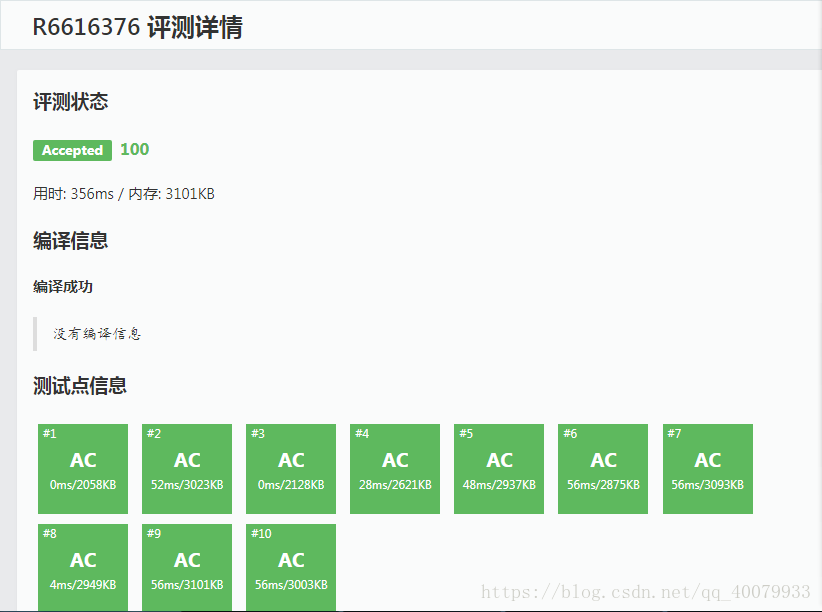
思路很简单,因为我们每一次插入一个点我们就对他进行旋转操作,旋转到根节点,然后查右子树大小就可以了。是不是很简单,但代码就比线段树难写太多了,但是还是比线段树快,内存也比线段树小!!!
上图:
代码如下:
#include<bits/stdc++.h>
using namespace std;
struct sd
{
int value;//当前节点所储存的值
int son[2];//左右儿子
int delta; //暂时没用
int father;//自己的爸爸
int below;//自己下面树的大小
}tree[1000005];
int root;//根
int cnt;//下标分配
int dir;//旋转方向 0是左边 1是右边
inline void maintain(int now)//维护 更新左右子树的大小(这道题中可以不写)
{
tree[now].below=1;
if(tree[now].son[0])tree[now].below+=tree[tree[now].son[0]].below;
if(tree[now].son[1])tree[now].below+=tree[tree[now].son[1]].below;
}
inline int get(int now)//确定旋转方向
{
if(tree[tree[now].father].son[0]==now)return 0;
return 1;
}
//----------------------------------------------------------------------
void rotate(int now)//旋转 需要重点理解
{
dir=get(now);
int fa=tree[now].father,gra=tree[fa].father;
tree[fa].son[dir]=tree[now].son[dir^1];
tree[tree[now].son[dir^1]].father=fa;
if(gra)tree[gra].son[get(fa)]=now;
tree[now].father=gra;
tree[fa].father=now;
tree[now].son[dir^1]=fa;
maintain(fa);
maintain(now);
}
//----------------------------------------------------------------------
inline void splay(int now)
{
int gra,fat;//定义now的祖父和爸爸
int opt1,opt2;//定义两次旋转方向
while(tree[now].father)//如果now还有自己的爸爸,即now还没有旋转到根节点。继续!
{
fat=tree[now].father;gra=tree[fat].father;
if(gra!=0)//如果有祖父,即要进行双旋!
{
opt1=get(now);opt2=get(fat);
if(opt1==opt2){rotate(fat),rotate(now);}
else{rotate(now),rotate(now);}
}
else
rotate(now);
}
root=now;//更新根节点
}
void insertit(int now,int val,int pre)
{
if(!now)//如果now为零(零是假的,其余是真的)说明他没有(左右)儿子,就插入,并且进行根节点旋转
{
cnt++;
tree[cnt].father=pre;
tree[cnt].value=val;
tree[cnt].below=1;
if(tree[pre].value>val)tree[pre].son [0]=cnt;
else tree[pre].son[1]=cnt;
splay(cnt);
}
else//如果now不是零
{
if(tree[now].value>val)insertit(tree[now].son[0],val,now);
else insertit(tree[now].son[1],val,now);
}
}
inline void in(int &x)//快读
{
bool fu=false;
x=0;char c=getchar();
while(!isdigit(c))
{
if(c=='-')
{
fu=true;
}
c=getchar();}
while(isdigit(c)){x*=10,x+=c-48;c=getchar();}
if(fu)x*=-1;
}
int main()
{
int ans=0;
long long tot=0;
int num,prev,sucv;
in(num);
int a;
while(num--)
{
in(a);
insertit(root,a,root);//读入(从当前根向下扔数)
ans+=tree[root].below-tree[tree[root].son[0]].below-1;//-1很重要
}
printf("%d",ans);//返回总和
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号