第九篇:使用 AdaBoost 元算法提高分类器性能
前言
有人认为 AdaBoost 是最好的监督学习的方式。
某种程度上因为它是元算法,也就是说它会是几种分类器的组合。这就好比对于一个问题能够咨询多个 "专家" 的意见了。
组合的方式有多种,可能是不同分类算法的分类器,可能是同一算法在不同设置下的集成,还可以是数据集在不同部分分配给不同分类器之后的集成等等。
本文将给出的 AdaBoost 分类器实现基于第二种 (另外几种实现在此基础上稍作改动即可)。
一种原始的元算法 - bagging (自举汇聚法)
这个算法的意思有点像投票系统,其思路步骤大致如下:
1. 将数据按照一定的规则划分成 N 份,每份的大小和原数据集一样大 (因此里面肯定是有重复数据的)。
2. 将这 N 份数据集分发到多个分类器中。
3. 按照 "少数服从多数" 原则,从这 N 个分类器的分类结果中总结出最优结果。
boost (提高任意给定学习算法精确度算法) vs bagging (自举汇聚法)
boost 和 bagging 一个很大的不同是它会给那些分错的样本更高关注度(权重)。AdaBoost 是一种最为典型的 boost 元算法。
因此理论上它能在相对较少的迭代次数下得到更为精确的分类结果。
AdaBoost 元算法的基本原理
AdaBoost 的强大之处,在于它能够集成多个弱分类器,形成一个强分类器。
所谓弱分类器就是分类错误率大于五成的分类器,比随机分类还渣。(但是它的分类算法是确定的,这点和随机分类器不同。显然你无法通过集成随机分类器得到什么有价值的东西)
其具体步骤大致如下:
1. 对每个样本给定一个权重 d。
2. 基于权重向量 D 调用一次弱分类器并得出这次统计的分类器权重值 alpha (注意是分类器权重值,区别于上一步的权重d)
3. 基于分类器权重值 alpha 更新各个样本的权重向量
4. 循环 2 - 3 直到错误率为 0 或者循环到了指定的次数
5. 1-4 为训练部分算法,训练好了之后,便可带入样本进行分类。分类的方法是依次带入训练集中的各个分类器中求出分类结果,然后各部分结果乘以其对应的分类器权重值 alpha 再累加求和。
下图可用来帮助理解 (直方图中的矩形长度表示样本权重,三角形中的值表示分类器权重值 alpha):
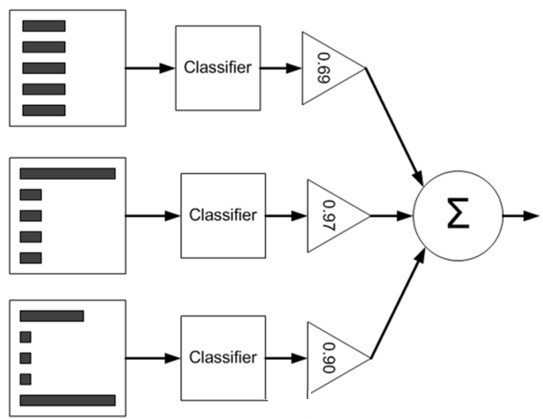
基于单层决策树的 AdaBoost 元算法分类器实现
首先,准备好单层决策树的数据结构。
在本文的 AdaBoost 实现中,元算法中的分类器组合模式是 "同一算法在不同设置下的集成",那么不同设置不同在哪里?
不同就不同在每次构建单层决策树都是选择划分正确率最高的划分方式。
因此在构建单层决策树函数中,必须有一个择优过程,具体可以参考下面的实现代码。
函数的功能应当是返回一个单层决策树信息结构(仅仅是划分信息就可以了不用数据)。
同时,函数应该返回一个错误信息值,这个错误值是和权重向量D相关的,用于计算分类器权重值 alpha。(当然也可以在该函数内部实现该字段)
最后,分类结果自然也要返回。
单层决策树代码实现如下:
1 #========================================== 2 # 输入: 3 # dataMatrix: 输入数据 4 # dimen: 划分特征下标 5 # threshVal: 划分阈值 6 # threshIneq: 划分方向(是左1右0分类还是左0右1分类) 7 # 输出: 8 # retArray: 分类结果 9 #========================================== 10 def stumpClassify(dataMatrix,dimen,threshVal,threshIneq): 11 '按照指定方式分类并返回结果' 12 13 retArray = numpy.ones((numpy.shape(dataMatrix)[0],1)) 14 if threshIneq == 'lt': 15 retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 16 else: 17 retArray[dataMatrix[:,dimen] > threshVal] = -1.0 18 19 return retArray 20 21 22 #========================================== 23 # 输入: 24 # dataArr: 输入数据 25 # classLabels: 分类标签集 26 # D: 权重向量 27 # 输出: 28 # bestStump: 决策树信息 29 # minError: 带权错误(用于生成分类器权重值 alpha) 30 # bestClasEst: 分类结果 31 #========================================== 32 def buildStump(dataArr,classLabels,D): 33 '创建单层最佳决策树' 34 35 dataMatrix = numpy.mat(dataArr); 36 labelMat = numpy.mat(classLabels).T 37 m,n = numpy.shape(dataMatrix) 38 39 # 特征值阈值步长 40 numSteps = 10.0; 41 # 当前最佳决策树信息集 42 bestStump = {}; 43 # 分类结果 44 bestClasEst = numpy.mat(numpy.zeros((m,1))) 45 # 最小带权错误初始化为无穷大 46 minError = numpy.inf 47 48 for i in range(n): # 遍历所有的特征选取最佳划分特征 49 rangeMin = dataMatrix[:,i].min(); 50 rangeMax = dataMatrix[:,i].max(); 51 stepSize = (rangeMax-rangeMin)/numSteps 52 53 for j in range(-1,int(numSteps)+1): # 遍历所有的特征值选取最佳划分特征值 stepSize为探测步长 54 55 for inequal in ['lt', 'gt']: # 对于 左1右0 和 左0右1 两种分类方式 56 57 # 当前划分阈值 58 threshVal = (rangeMin + float(j) * stepSize) 59 # 分类 60 predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal) 61 # 统计分类错误信息 62 errArr = numpy.mat(numpy.ones((m,1))) 63 errArr[predictedVals == labelMat] = 0 64 weightedError = D.T*errArr 65 66 # 更新最佳决策树的信息 67 if weightedError < minError: 68 minError = weightedError 69 bestClasEst = predictedVals.copy() 70 bestStump['dim'] = i 71 bestStump['thresh'] = threshVal 72 bestStump['ineq'] = inequal 73 74 return bestStump,minError,bestClasEst
在单层决策树之上,便是 AdaBoost 分类器的实现,下面先给出伪代码:
1 对每次迭代: 2 找到最佳单层决策树 3 将该树加入到最佳决策树数组 4 计算分类器权重 alpha 5 更新权重向量 D 6 更新累计类别估计值 7 PS: 如果错误率等于0.0,则立马退出循环。
Python 代码实现如下:
1 #========================================== 2 # 输入: 3 # dataArr: 输入数据 4 # classLabels: 分类标签集 5 # numIt: 最大迭代次数 6 # 输出: 7 # bestStump: 决策树信息 8 # minError: 带权错误(用于生成分类器权重值 alpha) 9 # bestClasEst: 分类结果 10 #========================================== 11 def adaBoostTrainDS(dataArr,classLabels,numIt=40): 12 'AdaBoost 分类器' 13 14 # 最佳决策树集合 15 weakClassArr = [] 16 # 样本个数 17 m = numpy.shape(dataArr)[0] 18 # 权重向量 19 D = numpy.mat(numpy.ones((m,1))/m) 20 # 各个类别的估计累积值 21 aggClassEst = numpy.mat(numpy.zeros((m,1))) 22 23 for i in range(numIt): # 迭代 numIt 次 24 # 构建最佳决策树 25 bestStump,error,classEst = buildStump(dataArr,classLabels,D) 26 # 计算该决策树的分类器权重值 alpha 27 alpha = float(0.5*numpy.log((1.0-error)/max(error,1e-16))) 28 bestStump['alpha'] = alpha 29 # 将该决策树加入到决策树数组中去 30 weakClassArr.append(bestStump) 31 32 # 更新权重向量 33 expon = numpy.multiply(-1*alpha*numpy.mat(classLabels).T,classEst) 34 D = numpy.multiply(D,numpy.exp(expon)) 35 D = D/D.sum() 36 37 # 计算当前的总错误率。如果错误率为0则退出循环。 38 aggClassEst += alpha*classEst 39 aggErrors = numpy.multiply(numpy.sign(aggClassEst) != numpy.mat(classLabels).T,numpy.ones((m,1))) 40 errorRate = aggErrors.sum()/m 41 print "错误率: ",errorRate 42 if errorRate == 0.0: break 43 44 return weakClassArr
至此,就可以用 AdaBoost 进行分类了。
首先训练出一个训练集,然后将训练集带入分类函数,如下:
1 # 获取训练集 2 classifierArr = adaBoostTrainDS(daaArr, labelArr, 30) 3 # 分类并打印结果 4 print adaClassify([0,0], classifierArr)
测试结果:

显然,可以看出 AdaBoost 分类器由三个决策树构成。样本最终分类结果为 -1。
小结
本文介绍了分类器中的元算法思想。通过这样的思想,能够将多种分类器组合起来,大大地加强了分类性能。
另外据可靠数据分析,较之逻辑回归,AdaBoost 分类器没有过度拟合(overfitting)现象。
Boost算法还有很多种,AdaBoost 只是其中最为经典的实现之一,还有更多高级实习需要在日后学习工作中进行研究。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号