1. 独立性的理解
“如果两个事件不能同时发生(P(AB)=0),那么它们一定互相独立吗?”
(甚至可以说,不可能同时发生,一定不独立);
独立性的判断只有一个标准:
考虑如下的两个事件,A:骰子掷出的点数为 6,B:掷出的点数为奇数,显然 AB 不可能同时发生,P(AB) = 0,又 P(A) = 1/6, P(B) = 1/2,显然 P(AB) ≠ P(A)P(B)。
那么的话,独立性该如何理解呢,
- 我怎么变化,与你怎么变化,没有关系,whatever,反之亦然;
- 与能不能同时发生,没有关系;
- A、B 不能同时发生,P(AB) = 0,AB 能同时发生 P(AB)>0
2. 独立与条件概率
A、B 两事件彼此独立(不具有依存关系):
一件事发生两次的概率与一件事再次发生的概率?:
- 一件事发生两次:抛两次硬币,都是正面朝上,1/4;两架飞机都失事;
- 一件事再次发生:第一次得到是正面向上,则下一次还是正面向上的概率为 1/2;飞机已经失事,再次失事;
3. P(A|B)与P(AB)
- P(AB) 表示的是事件 A、B 同时发生的概率
- P(B|A) 是指当事件 A 已经发生了(已知掷出的骰子是偶数),事件 B 发生的概率
4. 生活中的常见分布
正太分布无处不在。但生活中并不全是正太分布。
- 某医院某段时间,到达的人数 ⇒ 泊松分布
- 在全世界随意挑选一个人,他的性伴侣数量超过
x 的可能性为x−α
α 直接来自数据,举例发现瑞典女人的α=2.1 ,则从人群中找到一个拥有大于 100 个性伴侣的人的概率 6/10000;
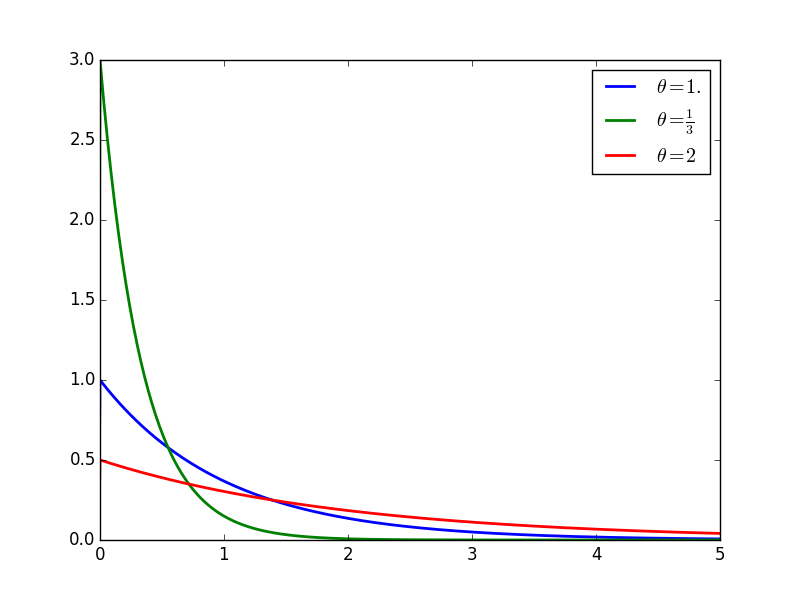
酒瓶摔到地上
酒瓶摔到地上,碎片的大小服从指数分布(Exponential distribution),粗略地讲,就是越大的碎片越少,越小的碎片越多。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号