这里有一篇十分精彩、生动的 并查集详解 (转);
- “朋友的朋友就是朋友”⇒ 传递性,建立连通关系
disjoint set,并查集(一种集合),也叫不相交集,同时也是一种树型的数据结构;用于处理一些不相交集合(Disjoint Sets)的合并(merge)及查询(find)问题。常常在使用中以森林来表示。集就是让每个元素构成一个单元素的集合,也就是按一定顺序将属于同一组的元素所在的集合合并。
并查集的构成:
整数型的数组
- 数组 pre[] 记录了每个点的前导点是什么,pred[] ⇒ 会形成一棵树形结构,树形结构的根,即为整棵树的代表(reps)
两个函数构成
- 函数 find 是查找;
- join 是合并;
1. 简单实现
find(暂不考虑,路径压缩的问题,path compression)
int pred[1000]; int find(int x){ int r = x; while (r != pred[r]){ r = pred[r]; } return r; }join
void find(int x, int y){ int rx = find(x), ry = find(y); if (rx != ry) pred[rx] = ry; // 因为 rx 是 x 等的代表 ⇒ pred[rx] == rx // 如此以来,x 所在的树,y 所在的树就实现了连通; }
2. 含有路径压缩的实现
路径压缩的概念可通过下图清晰地展示出来,
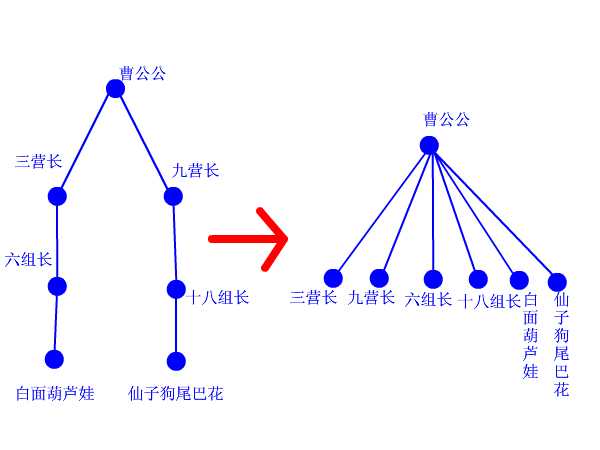
路径压缩之后,减少了中间的传递过程,一步直达根节点(总代表);
但需要注意的是,执行一次 find,只把一个分支,统一化为两层结构;
int find(int x)
{
int r=x;
while(r!=pre[r])
r=pre[r];
int i=x,j;
while(pre[i]!=r)
{
j=pre[i];
pre[i]=r;
i=j;
}
return r;
} 


 浙公网安备 33010602011771号
浙公网安备 33010602011771号