1. 定义
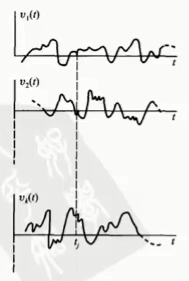
设
t 是时间,可以连续,也可为离散;X 为状态,可以连续,也可为离散;- 掷硬币(离散状态),电压值的变化(连续状态)
一般我们在理解时,成
时间集的不同类型:
[0,∞) :从当前时刻向前延伸;(−∞,∞) :既可以向前,也可以向后;(a,b) :某一个时间段(当然也可以是闭集合){0,1,…,n} :离散时间(有限或者无限)
2. 多维随机变量与随机过程
多维随机变量
(ξ1(w),ξ2(w),…,ξn(w)) ,其联合分布函数为:F(x1,x2,…,xn)=P(ξ1(w)≤x1,ξ2(w)≤x2,…,ξn(w)≤xn) 不同的随机变量的联合;
随机过程,
{Xt;t∈T} ,不再是分布函数,而是联合分布族(这里族对应的英文概念为 family,之所以称其为族,在于n 可以变化,n≥1 ):F(t1,t2,…,tn,x1,x2,…,xn)=P(Xt1(w)<x1,…,Xtn(w)<xn) 同一随机过程在不同时刻得到不同的随机变量;
3. 联合分布族的性质
对称性: 对
(1,2,…,n) 的任一排列(j1,j2,…,jn) 有:F(tj1,tj2,…,tjn;xj1,xj2,…,xjn)=F(t1,t2,…,tn;x1,x2,…,xn)
在n 个时间点上所取得的n 个随机变量构成的联合分布(事件的相对顺序对概率没有影响,A\cap B = B \cap AA∩B=B∩A )相容性:对任意 1\leq m\lt n
1≤m<n 和 X_1, \ldots, X_n\in RX1,…,Xn∈R 有:F(t_1, t_2, \ldots, t_m, t_{m+1}, \ldots, t_n; x_1, \ldots, x_m, \infty, \infty)=F(t_1, t_2, \ldots, t_m, t_{m+1}, \ldots, t_n; x_1, \ldots, x_m)
F(t1,t2,…,tm,tm+1,…,tn;x1,…,xm,∞,∞)=F(t1,t2,…,tm,tm+1,…,tn;x1,…,xm)
也即是 nn 维退化为 mm 维联合分布;
证明方法还是根据定义,F(t_1, t_2, \ldots, t_m, t_{m+1}, \ldots, t_n; x_1, \ldots, x_m)=P(X_1\lt x_1, X_2\lt x_2, \ldots, X_n \lt \infty)F(t1,t2,…,tm,tm+1,…,tn;x1,…,xm)=P(X1<x1,X2<x2,…,Xn<∞)
4. 随机过程的分类
- 独立增量过程:对任意的
t0<t1<⋯<tn,ti∈T,i=1,2,…,n ,如果Xt1−Xt0,⋯,Xtn−Xtn−1 是独立增量。
- 平稳独立增量过程(平稳就是某种意义上的不变),时间差一定 ⇒
- 平稳过程:
- 强平稳过程:
(Xt1+h,Xt2+h,…,Xtn+h) 都是同分布的,也即不随时间单位的平移而改变,也与平移任何的时间单位无关,联合分布都是同分布的; - 弱平稳过程:二阶矩过程,任意时间
EX2t<∞ ,且C(s,t)=EXsXt−EXsEXt 仅依赖于|t−s| (两个随机变量的协方差)(既然具有平稳性,就要求某个性质不变);
- 强平稳过程:
- 更新过程:是在计数过程(点过程)概念的基础上定义的,也即需对计数过程强加一些新的限制,事件间的时间间隔(
t2−t1,t3−t2,…,tn−tn−1 )独立同分布;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号