- 创新点的一般方向:
- ⇒ Generalized:泛化
- fixed ⇒ Adaptive,自适应(自调节)
- local adaptive
- hard ⇒ soft(threshold)
- single ⇒ local,individual ⇒ others;
- ⇒ Marginalized,⇒ Modified:修正的
- straightforward ⇒ iteration,直接求解,迭代求解;
- linear ⇒ non-linear,线性 ⇒ 非线性;
- 做距离度量(或者其他运算)时,仅考虑两个样本,而不考虑同一样本空间的其他样本
- 在做两个样本的距离度量(或者其他运算),不仅考虑此两个样本,还综合考虑同一样本空间的其他全部样本(显然样本之间存在 relation,相关性),使用 K-NN 算法选出距离最近的样本,比如著名的马氏距离;
1. Dictionary Learning(字典学习)
字典学习是图像的稀疏表示(sparse representation)的重要处理方法。K-SVD 字典学习又是字典学习理论的核心模型。
给定如下参数:
X=[x1,x2,…,xN] ,样本集;D=[d1,d2,…,dm] ,过完备字典;A=[α1,α2,…,αN] ,学习到的 sparse decomposition coefficients
传统的字典学习目标函数如下:
改进的思路:增加约束(正则化项):
保角约束(angle-preserving,conformal):
minD,α∑i∥xi−Dαi∥2+λ1∑i∥αi∥2+λ2f(α) 如何定义这里的
f(α) 呢。字典学习的过程就是zi=g(xi) ,X 空间向Z 空间的映射过程,我们首先找到通过 K-NN 的方法在样本空间(sample set)中寻找离当前样本xi 最近的两个样本xj 和xk ,其对应的Z 空间中的元素为zi,zj,zk ,保角特性要求∥xi−xj∥2∥zi−zj∥2=∥xi−xk∥2∥zi−zk∥2=∥xk−xj∥2∥zk−zj∥2=si
进一步转化为:∑j,k∈N(∥xj−xk∥2−si∥zj−zk∥2)2 则
f(αi) 的形式为:f(αi)=∑j,k∈N(∥xj−xk∥2−si∥αj−αk∥2)2 A 的低秩(low-rank)约束:minD,α∑i∥xi−Dαi∥2+λ1∑i∥αi∥2+λ2f(α)+λ3∥A∥⋆
参见论文:Conformal and Low-Rank Sparse Representation for Image Restoration.
2. 软硬阈值
- 硬阈值函数:
软阈值函数:
dj,k^=⎧⎩⎨⎪⎪dj,k−λ,dj,k≥λ0,otherwisedj,k+λ,dj,k≤−λ 当然也可转换为一个更为简洁的写法:
dj,k^={sign(dj,k)(|dj,k|−λ),|dj,k|≥λ0,otherwise
改进的思路:继续对阈值函数进行调整:
- 简单的线性叠加(linear):
αf1+(1−α)f2 非线性的构造方法(nonlinear,使其具有更快或者更为舒缓的衰减函数,当然选择指数函数:
ex )


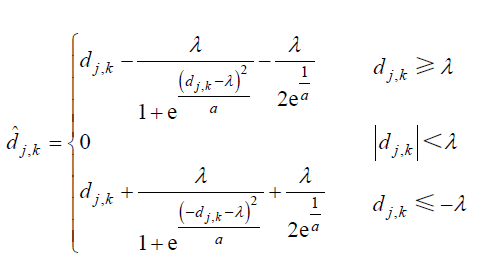

 浙公网安备 33010602011771号
浙公网安备 33010602011771号