1. RBM 的提出
BM 的缺点:
- 计算时间漫长,尤其是无约束自由迭代的负向阶段;
- 对抽样噪音敏感;
- 流行软件的不支持;
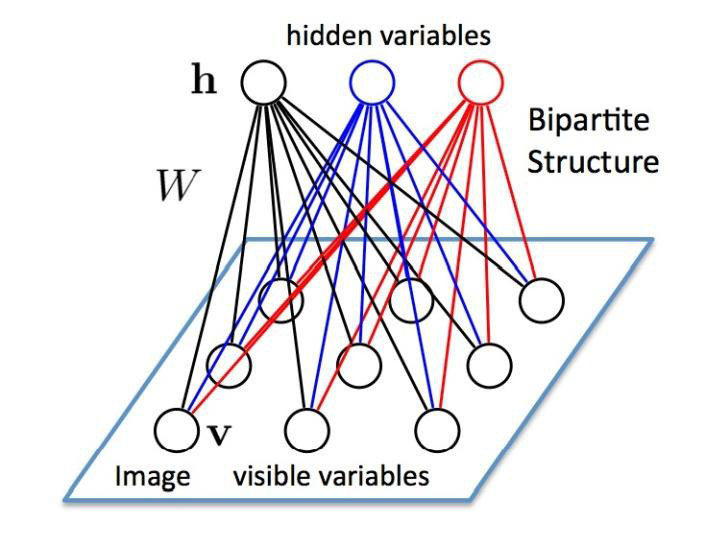
受限玻尔兹曼机(Restricted Boltzmann Machine,简称 RBM,以解决 BM 的学习效率过慢的严重缺陷)是由 Hinton 和 Sejnowski 于 1986 年提出的一种生成式随机神经网络(generative stochastic neural network),该网络由一些可见单元(visible unit,对应可见变量,亦即数据样本)和一些隐藏单元(hidden unit,对应隐藏变量)构成,可见变量和隐藏变量都是二元变量,亦即其状态取{0,1}。整个网络是一个二部图,只有可见单元和隐藏单元之间才会存在边,可见单元之间以及隐藏单元之间都不会有边连接,如下图所示:
2. BM 与 RBM 的对比
RBM 和 BM 一样,都可视为一种无向图(undirected graph),所谓无向的涵义即在于,权值对称,
wji=wij (自然对于有向图而言,与指向有关;)RBM 同层节点之间没有连接(BM 有连接),
- 可见层,隐层:结点之间彼此独立(简化的思路)(条件独立假设),
3. 数学记号
能量函数的定义:
E(v,h|θ)=−∑iaivi−∑jbjhj−∑in∑jmaiWijbj - 显然可以将上述公式简化为:一种向量的记法;
ai :可见层的偏置(bias)bj :隐层的偏置(bias)- 竖线右边的
θ 就像条件概率的形式一样,一般理解为固定θ (θ={Wij,ai,bj} )的条件下,E 关于v,h 的函数;
v,h 的联合概率分布为(由玻尔兹曼分布而来):P(v,h)=e−E(v,h|θ)Z(θ) Z 十分难计算(2n+m 种组合)
4. CD 算法
目标函数,即在参数(
5. AE 与 RBM
- AE:
- 出于简化的考虑:输入层,隐层,输出层;
- 因为通过低维的隐层,可以重构出输出层,可见低维的隐层,是一种对输入本质特征的描述,又可从侧面说明,输入层是可以被压缩,也即存在冗余,进一步我们可认为其是可以被稀疏表示的;
- 平方损失,BP反向传播,
- RBM:
- 可见层,隐层,可见层,隐层 ,,, ,是一种横向的展开;
- 这种周期性的循环结构可以被视为:不同的可见层其实是相互重叠的;
- 可见层既作为输入,也作为输出,(之所以称其为可见层,隐层,而不是输入层,隐层,输出层,就在于,可见层既作为输入层,也作为输出层) -



 浙公网安备 33010602011771号
浙公网安备 33010602011771号