(多项式的)因式分解定理(factor theorem)是多项式剩余定理的特殊情况,也就是余项为 0 的情形。
0. 多项式长除法(Polynomial long division)
Polynomial long division - Wikipedia
![这里写图片描述]()
1. 因式分解定理
Factor theorem
该定理表达的是,多项式 f(x) 存在因子 x−k 当且仅当 f(k)=0(余数为 0,也即 k 是其根)。
对于多项式 f(x)=x3+7x2+8x+2,
- x−1 是否为其因子?f(1)≠0
- x+1 是否为其因子?f(−1)=0,故为其因子;
(多项式除法)又有 x3+7x2+8x+2x+1=x2+6x+2,因此 x+1 与 x2+6x+2 均为其因子。
2. 多项式余项定理
Polynomial remainder theorem
举例对于多项式 f(x)=x3−12x2−42,当除数为 x−3 时,商为 x2−9x−27,余项为 −123。也即,f(x)=(x−3)(x2−9x−27)−123。因此 f(3)=−123。
更为一般地,对于二次多项式 f(x)=ax2+bx+c,有如下的等式变换:
f(x)x−r=ax2+bx+cx−r=ax2−arx+arx+bx+cx−r=ax(x−r)+(b+ar)x+cx−r=ax+(b+ar)(x−r)+c+r(b+ar)x−r=ax+b+ar+c+r(b+ar)x−r=ax+b+ar+ar2+br+cx−r
所以:
f(x)=(x−r)(ax+b+ar)+ar2+br+c
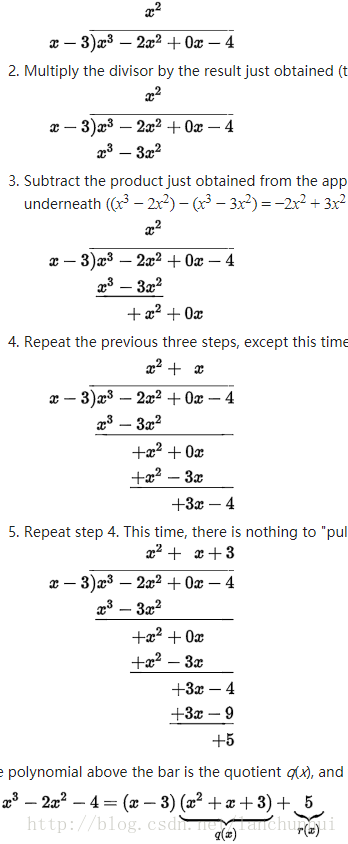


 浙公网安备 33010602011771号
浙公网安备 33010602011771号