Modeling one neuron
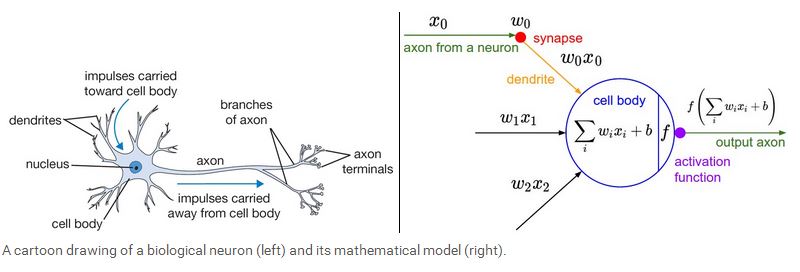
下面我们开始介绍神经网络,我们先从最简单的一个神经元的情况开始,一个简单的神经元包括输入,激励函数以及输出。如下图所示:
一个神经元类似一个线性分类器,如果激励函数是sigmoid 函数
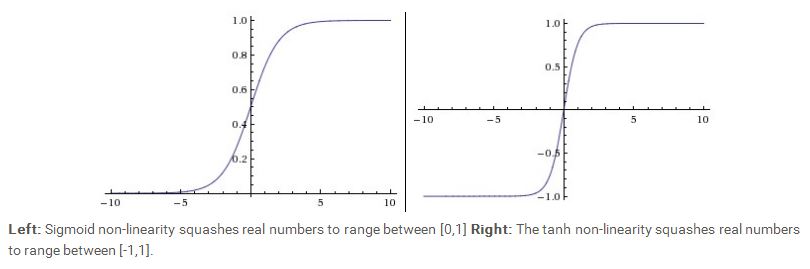
我们可以看到,sigmoid 函数的取值范围在(0,1)之间,而tanh 函数的取值范围在 (-1,1)之间。从图中可以看到,当sigmoid 函数的取值靠近0或者1时,它的梯度接近0,由于梯度在back propagation中有着非常重要的传递作用,因此如果梯度值太小,信息将无法传递。另外还有常见的几种激励函数比如Rectified Linear Unit(RLU),
我们将几种常见的激励函数归纳如下:
Sigmoid 函数:
tanh 函数:
RLU 函数:
Leak ReLU 函数:
maxout 函数:
Neural Network architectures
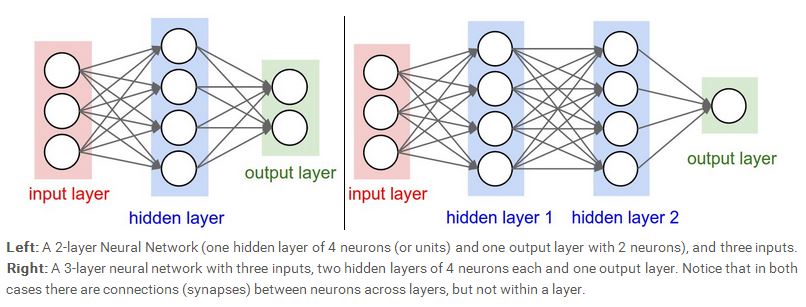
下面我们开始介绍神经网络,一个完整的神经网络包括输入层,隐含层,以及输出层。最常见的一种神经网络就是 fully-connected 型。如下图所示。我们可以看到,上一层的每一个神经元与下一层的每一个神经元都相连,左边的神经网络含有一个隐含层,右边的神经网络含有两个隐含层,当我们计算神经网络的层数时,我们会忽略输入层,所以左边的神经网络是一个两层的(一个隐含层加一个输出层),右边的神经网络是一个三层的(两个隐含层加一个输出层),输出层有的时候可以含有激励函数,也可以不含有激励函数,看网络设计的需求而定。
那么,神经网络的presentation power到底有多大呢,理论上,一个只含一层隐含层的神经网络模型可以表示任何复杂的函数。所以在机器学习领域,还在争论的一个问题
就是有没有必要利用deep神经网络,既然一个隐含层的shallow神经网络已经足够应付所有复杂的函数,deep 神经网络的优势目前看来是一种经验上的观察,虽然在理论上
与shallow神经网络相比没有太大优势。而且在实际使用中,三层的神经网络比两层的性能要好,但是再深一点的神经网络,比如四,五,六层的神经网络性能已经没有什么
提高了,这点与Convoluational 神经网络有点不太一样,在Convoluational 神经网络结构中,deepth 是一个很重要的保证网络性能的指标。
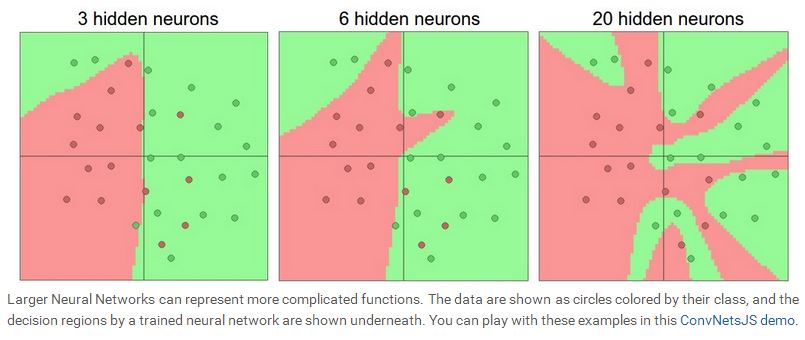
我们在设计神经网络的时候,要根据实际的问题,选择神经网络的结构,层数,隐含层神经元的个数,因为输入层和输出层基本由问题本身决定。一般来说,随着隐含层数的增加,以及隐含层里神经元个数的增加,网络的representation power会越大。我们可以看看如下的示例图。下图表示的是一个二分类问题,红点表示一类,绿点表示另外一类,利用一个两层的神经网络去学习这些数据,我们看到,随着神经元个数的增加,网络的拟合功能越来越强,当N=20时,所有的红点与绿点都完全区分开来了,所以说,神经元越多,网络就能表示越复杂的函数,但是随之而来的另外一个问题就是overfitting,如果一个网络过于专注数据中的噪声,而忽略了数据潜在的联系,就会出现overfitting。如下图所示,当N=20时,网络可以拟合所有的红点,但是却将平面分割地支离破碎,这种情况下,虽然网络的拟合能力很好,但是generalization能力却很差,意味着测试的性能会很糟糕。从这个例子看来,当数据不是很复杂的时候,似乎小的神经网络可以更好的控制overfitting的问题,但是事实上并非如此,我们一般不会用减少神经元个数的方法来控制overfitting,我们会用很多其他的方法来控制(比如 L2 regularization, dropout, input noise),这些会在后面的课程中介绍。
事实上,小规模的神经网络的一个缺点在于训练的难度,因为小的神经网络representation power有限,所以训练的自由度也相对较小,用梯度下降算法训练的时候,有可能陷入局部最小值,小规模的神经网络的局部最小值相对也较少,但是可能会很快收敛到这些局部最小值,这些极值有些会使网络的性能会很好,但是有些可能让网络性能很差,而大规模的神经网络局部最小值会很多,而且这些与实际误差相关的局部最小值会使网络的性能相对稳定。一般来说,小规模的神经网络性能会有很大的起伏,有的时候严重依赖于权值的初始值,而大规模的神经网络性能相对稳定,对权值的初始值依赖较少。
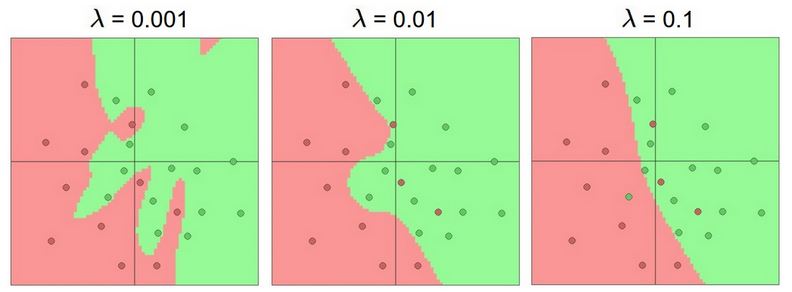
事实上,我们会利用regularization 去控制大规模网络的overfitting问题,下图给出了引入regularization 之后,N=20的神经网络的训练结果:
我们看到,随着regularization的增加,神经网络的分界面越来越平滑。
声明:lecture notes里的图片都来源于该课程的网站,只能用于学习,请勿作其它用途.
如需转载,请说明该课程为引用来源。http://cs231n.stanford.edu/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号