Hidden Markov Models
下面我们给出Hidden Markov Models(HMM)的定义,一个HMM包含以下几个要素:
值得注意的一点是,这里面定义的概率都是与时间不相关的,意味着这些概率不会随着时间的变化而变化,这一点假设与实际情况不符合,但是将问题大大简化了。
如果一个系统可以用HMM来描述,那么HMM模型可以解决三类问题:
Evaluation:
通过HMM得到可观察变量的概率。这类问题属于识别问题,假设我们有很多描述不同系统的
HMM模型,和一组观察变量,我们想知道哪个HMM模型与这组观察变量最匹配,及最有可能生成这组观察变量。我们会用一种forward算法去计算每个HMM模型生成这组观察变量的概率,然后挑选生成概率
最大的HMM模型。这类问题最常见的是用于语音识别,语音识别会用到很多HMM模型,每个HMM模型都modeling一个特定的词汇,而观察变量就是一个说出口的词汇,那么找出最有可能生成这个词汇的HMM,从而确认该词汇是什么。
Decoding:
找到最可能生成可观察变量的隐藏变量。这是第二类问题,一般是寻找隐藏变量,通过观察变量,寻找隐藏变量。比如最初的天气系统,我们能够利用的观察变量(海草的状态),但是我们希望预测的是隐藏变量(天气)。我们会介绍Viterbi算法来解决这类问题。
Learning:
给定可观察变量,生成一个HMM。第三类问题,通常是最困难的一类问题,就是通过一组观察变量,以及观察变量与隐藏变量的关系(这里的关系不是转换矩阵,只是观察变量与隐藏变量的相关性),确定一个最佳的HMM模型,也就是要求出HMM的
(πi,A,B) 。我们会介绍forward-backward算法来解决这类问题。
接下来,我们将详细讨论这三类问题和相应的算法。
Forward Algorithm
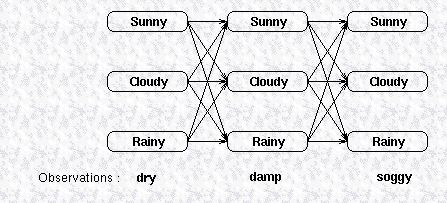
第一类问题是给定HMM模型,求解可观察变量的概率,我们仍然以天气预测为例,假设我们有一个HMM模型描述天气之间的转换关系,以及天气与海草的状态之间关系,现在我们有一组观察变量,比如说海草连续三天的状态,假设这三天的状态分别为(dry,damp,soggy),这三天的天气可能是晴天,雨天或多云的任何一种,我们用下图表示天气
与海草的状态之间的关系:
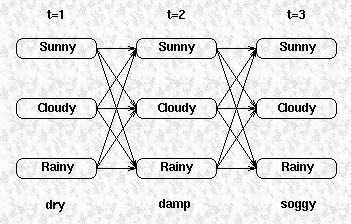
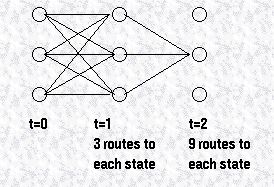
图中上面三行的每一列显示了可能的天气,而天气的每一个状态又会影响到下一天的天气状态,所以它们之间相互连接,天气之间的转换关系由状态转换矩阵给出,最下面一行是观察变量,隐藏变量生成观察变量的概率由confusion矩阵给出。要计算这个HMM模型生成观察变量的概率,最直观的一种方式是把所有可能路径的概率相加,在图上所示的模型里,有27种路径,所有要把27个概率之和相加,这显然是非常耗时的。
所以,我们换个角度考虑,我们采用一种递归的方式去计算观察变量的概率,我们先定义一个局部的概率用来表示马尔科夫过程到达一个中间状态的概率,我们先来看看如何计算这些中间概率,假设整个可观察变量序列长度为T,
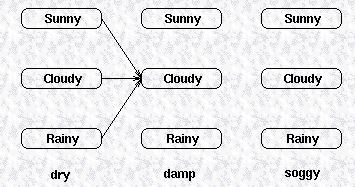
所有到达Cloudy的路径可以由下图表示:
我们定义状态
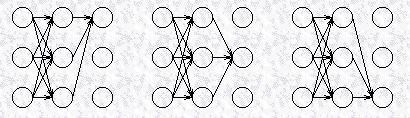
由此类推,该观察序列里,最后一个观察变量所对应的几个隐藏变量的局部概率包括了该HMM模型中,所有路径的概率之和,下图给出了该HMM模型最后一列状态的局部概率,
可以看到,该局部概率包括了该HMM模型的所有路径,所以这些局部概率之和就等于所有路径的概率之和,也就等于该HMM模型所生成的观察变量序列的概率。
虽然我们给出状态
我们已经给出了隐藏变量在初始状态的局部概率,也给出了隐藏变量在后续时刻的局部概率为:
随着时序的增加,我们可以看到,要计算的路径会以指数级增长,但是由于这些局部概率之间存在的递归关系,我们可以用下列式子表示
概率的关系:
通过这几个表达式,我们可以计算一个观察序列在
我们重新总结一下这个算法,利用forward算法计算一个时序长度为T的观察序列的概率,观察序列我们定义为如下所示:
其中,
而最终该观察序列的概率为:
所以通过给定的HMM模型,我们可以计算一个观察序列的概率。如果给定了一个观察序列,想要找到最匹配该观察序列的HMM模型,我们可以选择生成该观察序列的概率最高的HMM模型。
参考来源:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号