1. 什么是代价函数
在线性回归中我们有一个像这样的训练集，m代表了训练样本的数量，比如 m = 47。而我们的假设函数， 也就是用来进行预测的函数，是这样的线性函数形式
，
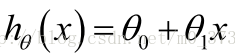，则代价函数可以表示为：
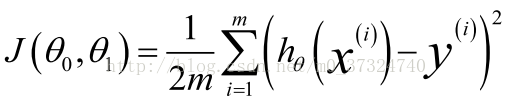
我们绘制一个等高线图，三个坐标分别为θ0 和θ1 和 J(θ0,θ1)：
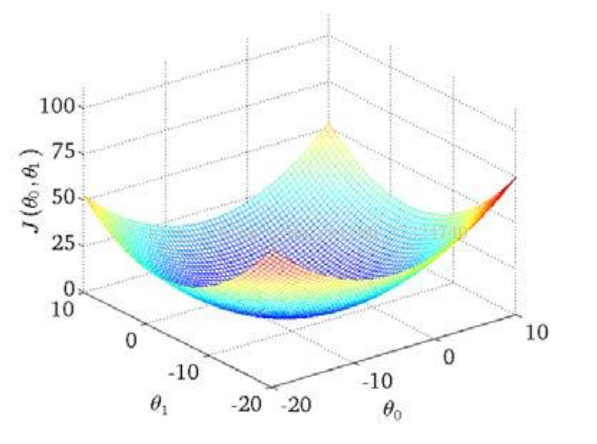
则可以看出在三维空间中存在一个使得 J(θ0,θ1)最小的点。
代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合 理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。
2. 梯度下降法
2.1 梯度下降概念
梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数J(θ0,θ1) 的最小值。 梯度下降背后的思想是：开始时我们随机选择一个参数的组合（θ0,θ1,...,θn），计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定 我们得到的局部最小值是否便是全局最小值（global minimum） 选择不同的初始参数组合， ，可能会找到不同的局部最小值。
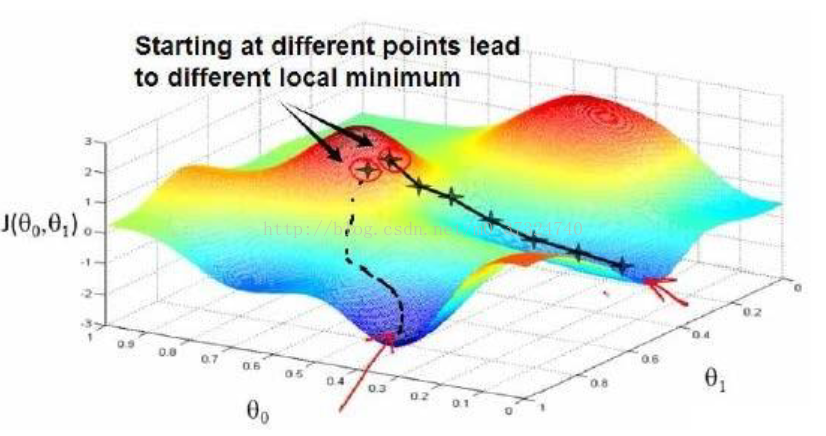
想象一下你正站立在山的这一点上，站立在你想象的公园这座红色山上，在梯度下降算法中，我们要做的就是旋转360度，看看我们的周围，并问自己要在某个方向上，用小碎步 尽快下山。这些小碎步需要朝什么方向？如果我们站在山坡上的这一点，你看一下周围，你 会发现最佳的下山方向，你再看看周围，然后再一次想想，我应该从什么方向迈着小碎步下 山？然后你按照自己的判断又迈出一步，重复上面的步骤，从这个新的点，你环顾四周，并 决定从什么方向将会最快下山，然后又迈进了一小步，并依此类推，直到你接近局部最低点 的位置。
2.2 梯度下降算法
算法公式为：
其中 α 是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方 向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
在梯度下降算法中，还有一个更微妙的问题，梯度下降中，我们要更新θ0和θ1 ，当 j=0和 j=1 时，会产生更新，所以你将更新Jθ0和Jθ1。实现梯度下降算法的微妙之处是，在这 个表达式中，如果你要更新这个等式， 你需要同时更新θ0和θ1。同步更新是更自然的实现方式，这里不详细介绍。
2.3 算法的直观理解
我想找到它的最小值，首先初始化我的梯度下降算法，在那个品红色的点初始化，如果我更新一步梯度下降，也许它会带我到这个点，因为这个点的导数是相当陡的。现在，在这 个绿色的点，如果我再更新一步，你会发现我的导数，也即斜率，是没那么陡的。随着我接 近最低点，我的导数越来越接近零，所以，梯度下降一步后，新的导数会变小一点点。然后 我想再梯度下降一步，在这个绿点，我自然会用一个稍微跟刚才在那个品红点时比，再小一 点的一步，到了新的红色点，更接近全局最低点了，因此这点的导数会比在绿点时更小。所 以，我再进行一步梯度下降时，我的导数项是更小的，θ1更新的幅度就会更小。所以随着 梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，你会发现，已经收敛到局部极小值。
如果α太小了，即我的学习速率太小，结果就是只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果α太小的话，可能会很慢 因为它会一点点挪动，它会需要很多步才能到达全局最低点。 如果α太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移 动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果α太大，它会导致无法收敛，甚至发散。
另外，假设你将θ1初始化在局部最低点，在这儿， 它已经在一个局部的最优处或局部最低点。结果是局部最优点的导数将等于零，因为它是那条切线的斜率。这意味着你已经在局部最优 点，它使得θ1不再改变，也就是新的θ1等于原来的θ1，因此，如果你的参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。这也解释了为什么即 使学习速率α保持不变时，梯度下降也可以收敛到局部最低点。
参考资料：斯坦福大学公开课：机器学习课程http://open.163.com/special/opencourse/machinelearning.html
