1. 逻辑回归
逻辑回归,该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是:
g 代表逻辑函数(logistic function)是一个常用的逻辑函数为S形函数 (Sigmoid function),公式为:

合起来,我们得到逻辑回归模型的假设模型:

2. 代价函数
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和,,我们 也可以对逻辑回归模型沿用这个定义,但是会得到一个非凸函数(non-convex function),如下图:
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。重新定义逻辑回归的代价函数为:
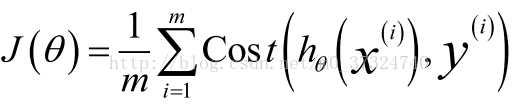
hθ(x)与 Cost(hθ(x),y)之间的关系如下图所示:
这样构建的Cost(hθ(x),y)函数的特点是: 当实际的 y=1 且hθ也为 1 时误差为 0,当 y=1,但hθ不为1时误差随着 hθ的变小而变大;当实际的 y=0 且hθ也为 0 时代价为 0,当 y=0 但 hθ不为0时误差随着 hθ的变大而变大。 将构建的 Cost(hθ(x),y)简化如下:
带入代价函数得到:
在得到这样一个代价函数以后, 我们便可以用梯度下降算法来求得能使代价函数最小的 参数了。算法为:
求导后得到:
参考资料:斯坦福大学公开课:机器学习课程http://open.163.com/special/opencourse/machinelearning.html


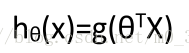

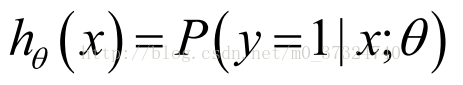

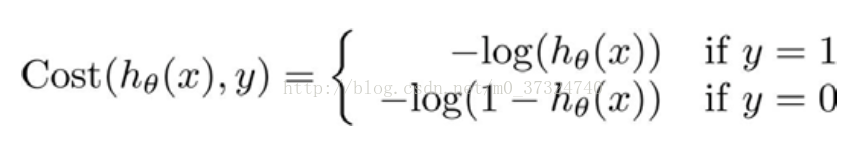

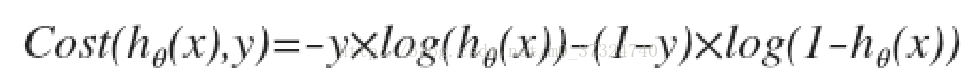
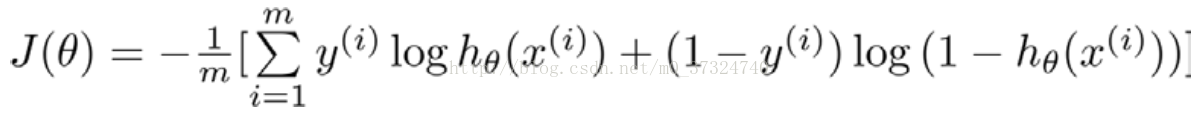



 浙公网安备 33010602011771号
浙公网安备 33010602011771号