开篇语:继上两篇博客介绍栈在符号匹配和进制转换中的应用后,本篇博客讲介绍栈在前缀、中缀、后缀转换中的应用。
1中缀、前缀、后缀概念介绍
中缀:算术表达式如 B*C中,乘法运算符 *为两个操作数之间的中缀。
问题:A+B*C,运算符 + 和 * 仍然出现在操作数之间。这里面有个问题是,他们分别作用于哪个运算数上,+ 作用于 A 和 B , 还是 * 作用于 B 和 C?表达式似乎有点模糊,计算机不知道运算符的优先级。
解决方法1:使用括号:唯一改变顺序的是括号的存在。因此,一种保证不会对操作顺序产生混淆的表达式的方法是创建一个称为完全括号表达式的表达式。如:
表达式 A+B*C+D 可以重写为 ((A + (B * C)) + D) ,表明先乘法,然后是左边的加法。
解决方法2:前缀和后缀表达式:中缀表达式 A+B, 如果我们移动两个操作数之间的运算符会发生什么?结果表达式变成 + A B。同样,我们也可以将运算符移动到结尾,得到 A B +。
前缀和后缀表达式规则:前缀表达式符号要求所有运算符在它们处理的两个操作数之前。另一个方面,后缀要求其操作符在相应的操作数之后。如下表:

更多例子:
2中缀表达式转换前缀和后缀
A + B * C可以写成(A +(B * C)),以明确标识乘法优先于加法。然而,仔细观察,你可以看到每个括号对还表示操作数对的开始和结束,中间有相应的运算符。
2.1中缀转换前缀
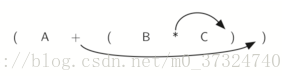
看上面的子表达式(B * C)中的右括号。 如果我们将乘法符号移动到那个位置,并删除匹配的左括号,得到 B C *,我们实际上已经将子表达式转换为后缀符号。 如果加法运算符也被移动到其相应的右括号位置并且匹配的左括号被去除,则将得到完整的后缀表达式如下:
2.2中缀转换后缀
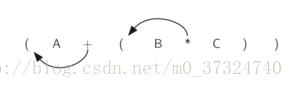
如果我们不是将符号移动到右括号的位置,我们将它向左移动,我们得到前缀符号如下(圆括号对的位置实际上是包含的运算符的最终位置的线索):
所以为了转换表达式,无论是对前缀还是后缀符号,先根据操作的顺序把表达式转换成完全括号表达式。然后将包含的运算符移动到左或右括号的位置,具体取决于需要前缀或后缀符号。
2.3中缀转后缀通用法
我们需要开发一个算法来将任何中缀表达式转换为后缀表达式。
首先我们观察规律,考虑表达式 A + B * C:
从左到右出现的第一个运算符为 +。 然而,在后缀表达式中,+ 在结束位置,因为下一个运算符 * 的优先级高于加法。 原始表达式中的运算符的顺序在生成的后缀表达式中相反。由于这种顺序的反转,考虑使用栈来保存运算符直到用到它们是有意义的。
(A + B)* C的情况会是什么样呢? 回想一下,A B + C 是等价的后缀表达式。从左到右处理此中缀表达式,我们先看到 +。 在这种情况下,当我们看到 ,+已经放置在结果表达式中,由于括号它的优先级高于*。 我们现在可以开始看看转换算法如何工作。当我们看到左括号时,我们保存它,表示高优先级的另一个运算符将出现。该操作符需要等到相应的右括号出现以表示其位置(回忆完全括号的算法)。 当右括号出现时,可以从栈中弹出操作符。具体步骤如下:
- 创建一个名为 opstack 的空栈以保存运算符。给输出创建一个空列表。
- 通过使用字符串方法拆分将输入的中缀字符串转换为标记列表。
- 从左到右扫描标记列表。
如果标记是操作数,将其附加到输出列表的末尾。
如果标记是左括号,将其压到 opstack 上。
如果标记是右括号,则弹出 opstack,直到删除相应的左括号。将每个运算符附加到输出列表的末尾。
如果标记是运算符,*,/,+或 - ,将其压入 opstack。但是,首先删除已经在 opstack 中具有更高或相等优先级的任何运算符,并将它们加到输出列表中。 - 当输入表达式被完全处理时,检查 opstack。仍然在栈上的任何运算符都可以删除并加到输出列表的末尾。
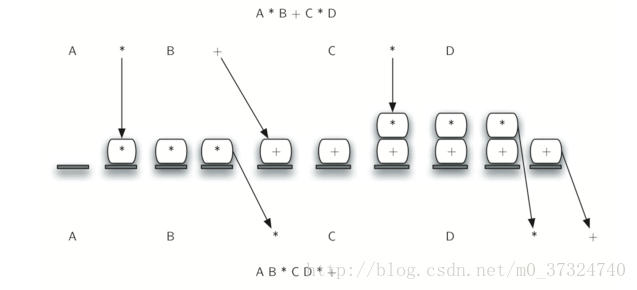
例子如下图:
注意,第一个 * 在看到 + 运算符时被删除。另外,当第二个 * 出现时, + 保留在栈中,因为乘法优先级高于加法。在中缀表达式的末尾,栈被弹出两次,删除两个运算符,并将 + 作为后缀表达式中的最后一个运算符。
为了在 Python 中编写算法,我们使用一个名为 prec 的字典来保存操作符的优先级。这个字典将每个运算符映射到一个整数,可以与其他运算符的优先级(我们使用整数3,2和1)进行比较。左括号将赋予最低的值。实现代码如下:
from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
tokenList = infixexpr.split()
for token in tokenList:
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while (not opStack.isEmpty()) and \
(prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return " ".join(postfixList)3后缀表达式求值
以后缀表达式 4 5 6 * +为例:
首先遇到操作数 4 和 5,此时,你还不确定如何处理它们,直到看到下一个符号。将它们放置到栈上,确保它们在下一个操作符出现时可用。在这种情况下,下一个符号是另一个操作数。所以,像先前一样,压入栈中。并检查下一个符号。现在我们看到了操作符 *,这意味着需要将两个最近的操作数相乘。通过弹出栈两次,我们可以得到正确的两个操作数,然后执行乘法(这种情况下结果为 30)。我们现在可以通过将其放回栈中来处理此结果,以便它可以表示为表达式后面的运算符的操作数。当处理最后一个操作符时,栈上只有一个值,弹出并返回它作为表达式的结果。整个过程如下所示:
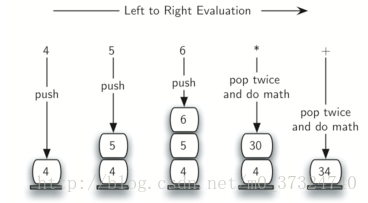
具体步骤:
假设后缀表达式是一个由空格分隔的标记字符串。 运算符为*,/,+和 - ,操作数假定为单个整数值。 输出将是一个整数结果。
1. 创建一个名为 operandStack 的空栈。
2. 拆分字符串转换为标记列表。
3. 从左到右扫描标记列表。
如果标记是操作数,将其从字符串转换为整数,并将值压到operandStack。
如果标记是运算符*,/,+或-,它将需要两个操作数。弹出operandStack 两次。 第一个弹出的是第二个操作数,第二个弹出的是第一个操作数。执行算术运算后,将结果压到操作数栈中。
4. 当输入的表达式被完全处理后,结果就在栈上,弹出 operandStack 并返回值。
实现代码如下:
from pythonds.basic.stack import Stack
def postfixEval(postfixExpr):
operandStack = Stack()
tokenList = postfixExpr.split()
for token in tokenList:
if token in "0123456789":
operandStack.push(int(token))
else:
operand2 = operandStack.pop()
operand1 = operandStack.pop()
result = doMath(token,operand1,operand2)
operandStack.push(result)
return operandStack.pop()
def doMath(op, op1, op2):
if op == "*":
return op1 * op2
elif op == "/":
return op1 / op2
elif op == "+":
return op1 + op2
else:
return op1 - op2
print(postfixEval('7 8 + 3 2 + /'))参考资料:《problem-solving-with-algorithms-and-data-structure-using-python》
http://www.pythonworks.org/pythonds




 浙公网安备 33010602011771号
浙公网安备 33010602011771号