希尔排序（有时称为“递减递增排序”）通过将原始列表分解为多个较小的子列表来改进插入排序，每个子列表使用插入排序进行排序。 选择这些子列表的方式是希尔排序的关键。不是将列表拆分为连续项的子列表，希尔排序使用增量i（有时称为 gap），通过选择 i 个项的所有项来创建子列表。
以i=3为例，下图显示了三个子列表的插入排序过程：
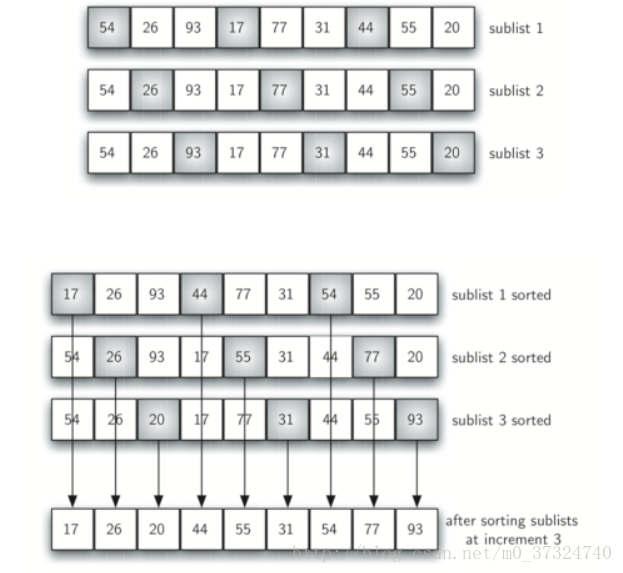
虽然这个列表没有完全排序，但发生了很有趣的事情。 通过排序子列表，我们已将项目移动到更接近他们实际所属的位置。
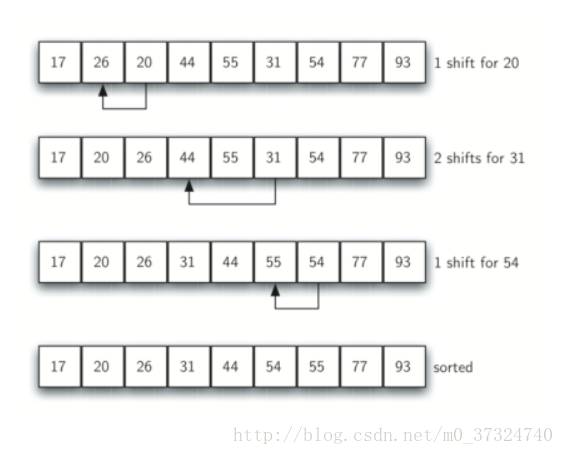
下图展示了使用增量为 1 的插入排序; 换句话说，标准插入排序。
注意，通过执行之前的子列表排序，我们减少了将列表置于其最终顺序所需的移位操作的总数。对于这种情况，我们只需要四次移位完成该过程。
python实现代码如下：
def shellSort(alist):
sublistcount = len(alist)//2
while sublistcount > 0:
for startposition in range(sublistcount):
gapInsertionSort(alist,startposition,sublistcount)
print("After increments of size",sublistcount,
"The list is",alist)
sublistcount = sublistcount // 2
def gapInsertionSort(alist,start,gap):
for i in range(start+gap,len(alist),gap):
currentvalue = alist[i]
position = i
while position>=gap and alist[position-gap]>currentvalue:
alist[position]=alist[position-gap]
position = position-gap
alist[position]=currentvalue
alist = [54,26,93,17,77,31,44,55,20]
shellSort(alist)
print(alist)乍一看，希尔排序不会比插入排序更好，因为它最后一步执行了完整的插入排序。 然而，结果是，该最终插入排序不需要进行非常多的比较（或移位），因为如上所述，该列表已经被较早的增量插入排序预排序。 换句话说，每个遍历产生比前一个“更有序”的列表。 这使得最终遍历非常有效。
参考资料：《problem-solving-with-algorithms-and-data-structure-using-python》
http://www.pythonworks.org/pythonds
