在介绍 python 实现图的深度优先和广度优先搜索前,我们先来了解下什么是“图”。
1 一些定义
顶点
顶点(也称为“节点”)是图的基本部分。它可以有一个名称,我们将称为“键”。
边
边(也称为“弧”)是图的另一个基本部分。边连接两个顶点,以表明它们之间存在关系。
权重
边可以被加权以示出从一个顶点到另一个顶点的成本。例如,在将一个城市连接到另一个城市的道路的图表中,边上的权重可以表示两个城市之间的距离。
利用这些定义,我们可以正式定义图。图可以由 G 表示,其中 G =(V,E)。对于图 G,V 是一组顶点,E 是一组边。每个边是一个元组 (v,w),其中 w,v ∈ V。我们可以添加第三个组件到边元组来表示权重。子图 s 是边 e 和顶点 v 的集合,使得 e⊂E 和 v⊂V 。
下图展示了简单加权有向图的另一示例。正式地,我们可以将该图表示为:
六个顶点的集合:
V={V0,V1,V2,V3,V4,V5};
9 条边的集合:
E={(v0,v1,5),(v1,v2,4),(v2,v3,9),(v3,v4,7),(v4,v0,1),(v0,v5,2),(v5,v4,8),(v3,v5,3),(v5,v2,1)}

2 常见的图结构
有两个众所周知的图形、实现,邻接矩阵和邻接表。
2.1 邻接矩阵
实现图的最简单的方法之一是使用二维矩阵。在该矩阵实现中,每个行和列表示图中的顶点。存储在行 v 和列 w 的交叉点处的单元中的值表示是否存在从顶点 v 到顶点 w 的边。 当两个顶点通过边连接时,我们说它们是相邻的。 下图展示了图的邻接矩阵。单元格中的值表示从顶点 v 到顶点 w 的边的权重。

邻接矩阵的优点是简单,对于小图,很容易看到哪些节点连接到其他节点。 然而,注意矩阵中的大多数单元格是空的。 因为大多数单元格是空的,我们说这个矩阵是“稀疏的”。矩阵不是一种非常有效的方式来存储稀疏数据。
2.2 邻接表
实现稀疏连接图的更空间高效的方法是使用邻接表。在邻接表实现中,我们保存 Graph 对象中的所有顶点的主列表,然后图中的每个顶点对象维护连接到的其他顶点的列表。 在我们的顶点类的实现中,我们将使用字典而不是列表,其中字典键是顶点,值是权重。
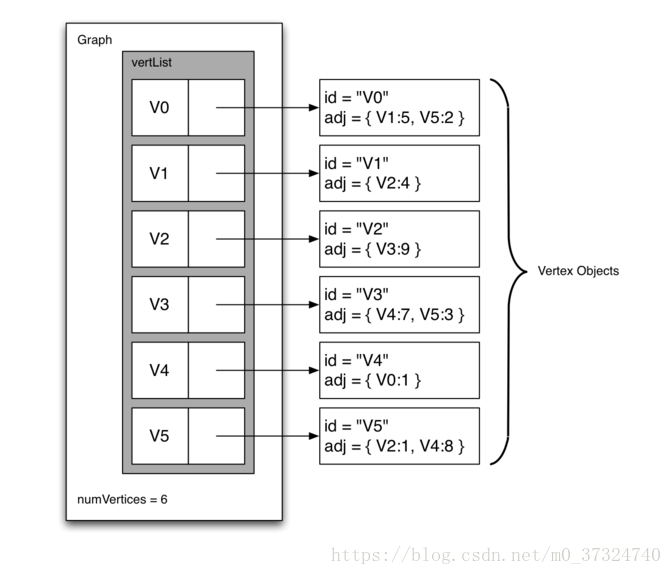
邻接表实现的优点是它允许我们紧凑地表示稀疏图。 邻接表还允许我们容易找到直接连接到特定顶点的所有链接。
3 python 实现图
在我们的 Graph 抽象数据类型的实现中,我们将创建两个类,Graph(保存顶点的主列表)和 Vertex(将表示图中的每个顶点)。每个顶点使用字典来跟踪它连接的顶点和每个边的权重。这个字典称 connectedTo 。
下面展示了 Vertex 类的代码。构造函数只是初始化 id ,通常是一个字符串和 connectedTo 字典。 addNeighbor 方法用于从这个顶点添加一个连接到另一个。getConnections 方法返回邻接表中的所有顶点,如 connectedTo 实例变量所示。 getWeight 方法返回从这个顶点到作为参数传递的顶点的边的权重。
class Vertex:
def __init__(self,key):
self.id = key
self.connectedTo = {}
def addNeighbor(self,nbr,weight=0):
self.connectedTo[nbr] = weight
def __str__(self):
return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
def getConnections(self):
return self.connectedTo.keys()
def getId(self):
return self.id
def getWeight(self,nbr):
return self.connectedTo[nbr]下面展示了 Graph 类的代码,包含将顶点名称映射到顶点对象的字典。Graph 还提供了将顶点添加到图并将一个顶点连接到另一个顶点的方法。getVertices方法返回图中所有顶点的名称。此外,我们实现了__iter__ 方法,以便轻松地遍历特定图中的所有顶点对象。 这两种方法允许通过名称或对象本身在图形中的顶点上进行迭代。
class Graph:
def __init__(self):
self.vertList = {}
self.numVertices = 0
def addVertex(self,key):
self.numVertices = self.numVertices + 1
newVertex = Vertex(key)
self.vertList[key] = newVertex
return newVertex
def getVertex(self,n):
if n in self.vertList:
return self.vertList[n]
else:
return None
def __contains__(self,n):
return n in self.vertList
def addEdge(self,f,t,cost=0):
if f not in self.vertList:
nv = self.addVertex(f)
if t not in self.vertList:
nv = self.addVertex(t)
self.vertList[f].addNeighbor(self.vertList[t], cost)
def getVertices(self):
return self.vertList.keys()
def __iter__(self):
return iter(self.vertList.values()) 我们用上面定义的两个类,建立如下的图结构。首先我们创建 6 个编号为 0 到 5 的顶点。然后我们展示顶点字典。注意,对于每个键 0 到 5,我们创建了一个顶点的实例。接下来,我们添加将顶点连接在一起的边。 最后,嵌套循环验证图中的每个边缘是否正确存储。

g = Graph()
for i in range(6):
g.addVertex(i)
g.addEdge(0,1,5)
g.addEdge(0,5,2)
g.addEdge(1,2,4)
g.addEdge(2,3,9)
g.addEdge(3,4,7)
g.addEdge(3,5,3)
g.addEdge(4,0,1)
g.addEdge(5,4,8)
g.addEdge(5,2,1)g.vertListfor v in g:
for w in v.getConnections():
print("( %s , %s )" % (v.getId(), w.getId()))
4 图的搜索
回溯法(探索与回溯法)是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
4.1 广度优先搜索
实现步骤:(1)顶点v入队列。
(2)当队列非空时则继续执行,否则算法结束。
(3)出队列取得队头顶点v;访问顶点v并标记顶点v已被访问。
(4)查找顶点v的第一个邻接顶点col。
(5)若v的邻接顶点col未被访问过的,则col入队列。
(6)继续查找顶点v的另一个新的邻接顶点col,转到步骤(5)。直到顶点v的所有未被访问过的邻接点处理完。转到步骤(2)。
实现代码:
from pythonds.graphs import Graph, Vertex
from pythonds.basic import Queue
def bfs(g,start):
start.setDistance(0)
start.setPred(None)
vertQueue = Queue()
vertQueue.enqueue(start)
while (vertQueue.size() > 0):
currentVert = vertQueue.dequeue()
for nbr in currentVert.getConnections():
if (nbr.getColor() == 'white'):
nbr.setColor('gray')
nbr.setDistance(currentVert.getDistance() + 1)
nbr.setPred(currentVert)
vertQueue.enqueue(nbr)
currentVert.setColor('black')


4.2 深度优先搜索
实现步骤:
(1)访问初始顶点v并标记顶点v已访问。
(2)查找顶点v的第一个邻接顶点w。
(3)若顶点v的邻接顶点w存在,则继续执行;否则回溯到v,再找v的另外一个未访问过的邻接点。
(4)若顶点w尚未被访问,则访问顶点w并标记顶点w为已访问。
(5)继续查找顶点w的下一个邻接顶点wi,如果v取值wi转到步骤(3)。直到连通图中所有顶点全部访问过为止。
实现代码:
由于 dfs 和它的辅助函数dfsvisit 这两个函数使用一个变量来跟踪调用 dfsvisit 的时间,所以我们选择将代码实现为继承自 Graph 类。此实现通过添加时间实例变量和两个方法 dfs 和 dfsvisit来扩展 Graph 类。看看第 11 行,你会注意到,dfs 方法在调用 dfsvisit 的图中所有的顶点迭代,这些节点是白色的。我们迭代所有节点而不是简单地从所选择的起始节点进行搜索的原因是为了确保图中的所有节点都被考虑到,没有顶点从深度优先森林中被遗漏。for aVertex in self 语句可能看起来不寻常,但请记住,在这种情况下,self是 DFSGraph 类的一个实例,遍历实例中的所有顶点是一件自然的事情。代码如下:
from pythonds.graphs import Graph
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time) 搜索过程如下图所示,初始点是白色,探索点是灰色,终结点是黑色



参考资料:《problem-solving-with-algorithms-and-data-structure-using-python》
http://www.pythonworks.org/pythonds





 浙公网安备 33010602011771号
浙公网安备 33010602011771号