用全连接神经网络做汽车效能的回归预测
用全连接神经网络做汽车效能的回归预测
keyword: 全连接神经网络,tensorflow, 回归
说明
主要是利用全连接神经网络来做汽车的效能指标MPG的回归问题预测。
python包包括:os, pandas, tensorflow, sklearn, matplotlib
数据加载
数据集为Auto MPG。主要是关于各种汽车的效能指标。
除了产地外,其他字段都是数值型。产地为类别型字段,1美国,2欧洲,3日本。
- MPG: 每加仑英里(效能指标,y)
- Cylinders: 气缸数
- Displacement: 排量
- Horsepower: 马力
- Weight: 重量
- Acceleration: 加速度
- Model Year: 型号年份
- Origin: 产地
import os
import pandas as pd
data_path = os.path.join(os.getcwd(), r'data\auto-mpg.data')
column_names = [
'MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin'
]
raw_data = pd.read_csv(
data_path, names=column_names,
na_values='?', comment='\t',
sep=' ', skipinitialspace=True
)
加载完成之后,一般也会对数据进行一些观察、备份等。
df.info()
df.head()
df.describe()
df.tail()
df.to_pickle(r'D:\data\auto-mpg.pkl')
数据处理
通过数据观察,发现数据存在缺失值。有一个字段origin是类别型数据。另外,用梯度下降来寻找最优参数,最好进行标准化处理。
缺失值处理
df.isna().sum()
选择直接删除。
df = df.dropna()
特征处理
# 处理类别型数据,其中 origin 列代表了类别 1,2,3,分布代表产地:美国、欧洲、日本
# 先弹出(删除并返回)origin 这一列
origin = df.pop('Origin')
# 根据 origin 列来写入新的 3 个列
df.loc[:, 'USA'] = (origin == 1)*1.0
df.loc[:, 'Europe'] = (origin == 2)*1.0
df.loc[:, 'Japan'] = (origin == 3)*1.0
数据划分和标准化
这里标准化,是直接按标准化的定义来处理。当然最简单可以直接使用sklearn.preprocessing.StandardScaler方法。
数据直接按8:2的比例划分训练集和测试集。
from sklearn.model_selection import train_test_split
# 按8:2的比例划分训练集和测试集
x_columns = df.columns.to_list()
x_columns.remove('MPG')
y_columns = ['MPG']
x_sample = df[x_columns]
y_sample = df[y_columns]
train_dataset, test_dataset, train_labels, test_labels = train_test_split(x_sample, y_sample, test_size=0.2, random_state=0)
数据进行标准化处理。
# 统计训练集各个字段数值的均值和标准差,完成数据的标准化
train_stats = train_dataset.describe()
train_stats = train_stats.transpose()
# 标准化数据
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
打印出训练集,测试集大小:
# 打印训练集和测试集的大小
print(f'训练集的大小为:{normed_train_data.shape}, 标签数量:{train_labels.shape}')
print(f'测试集的大小为:{normed_test_data.shape}, 标签数量:{test_labels.shape}')
数据观察
主要是通过对于数据特征的统计、作图等方法,对数据有更深的认识。从而有助于模型的选择,或做进一步的数据处理等。
特征名称:
normed_train_data.columns.to_list()
特征之间的散点图,观察特征之间的线性关系:
from pandas.plotting import scatter_matrix
attributes = [
'Cylinders',
'Displacement',
'Horsepower',
'Weight',
'Acceleration'
]
scatter_matrix(normed_train_data[attributes], figsize=(12, 8))
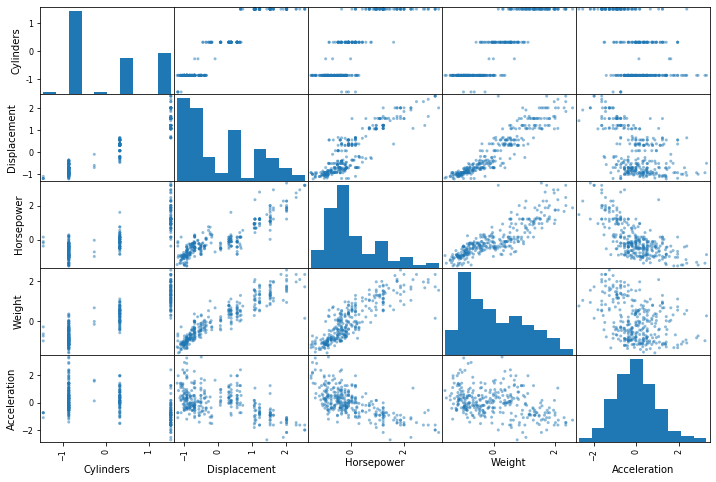
图1 特征之间的线性关系
观察特征与目标之间的线性关系。
df.plot.scatter(
x='Cylinders',
y='MPG'
)
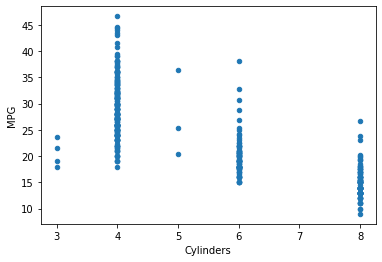
图2 特征与目标之间的线性关系
创建网络模型
由于数据量比较小,因此只创建一个3层的全连接网络来完成MPG的预测任务。
输入的特征为9,因此输入节点数为9. 中间两个隐藏层的输出节点数为64,64.由于只有一个预测值,因此输出层节点为1. 而且输出层为数值型预测,因此可以不加激活函数,或者添加ReLU激活函数。
tensorflow的网络构建方式是很灵活的,因此下面用几种方式来构建。
方式1
网络构建
from tensorflow.keras import layers
from tensorflow import keras
import tensorflow as tf
class Network(keras.Model):
# 回归网络
def __init__(self):
super(Network, self).__init__()
# 创建3个全连接层
self.fc1 = layers.Dense(64, activation='relu')
self.fc2 = layers.Dense(64, activation='relu')
self.fc3 = layers.Dense(1)
def call(self, inputs, training=None, mask=None):
# 依次通过3个全连接层
x = self.fc1(inputs)
x = self.fc2(x)
x = self.fc3(x)
return x
训练模型
model = Network()
# build函数来完成内部张量的创建,其中4为任意的batch数量,9为输入特征长度
model.build(input_shape=(4, 9))
# 打印网络信息
model.summary()
# 创建优化器,指定学习率
optimizer = keras.optimizers.RMSprop(0.001)
Model: "network_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_3 (Dense) multiple 640
_________________________________________________________________
dense_4 (Dense) multiple 4160
_________________________________________________________________
dense_5 (Dense) multiple 65
=================================================================
Total params: 4,865
Trainable params: 4,865
Non-trainable params: 0
构建Dataset对象:
# 数据
# 构建Dataset对象
train_db = tf.data.Dataset.from_tensor_slices((
normed_train_data.values,
train_labels.values
))
# 随机打散,批量化
train_db = train_db.shuffle(100).batch(32)
训练模型
loss_log = list()
i = 0
for epoch in range(100):
for step, (x, y) in enumerate(train_db):
# 梯度记录器
with tf.GradientTape() as tape:
out = model(x)
loss = tf.reduce_mean(tf.losses.MSE(y, out))
# mae_loss = tf.reduce_mean(tf.losses.MAE(y, out))
i += 1
loss_log.append([i, float(loss)])
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
参数查看
对于回归问题,评价指标一般有MSE(均方误差), RMSE(均方根误差), MAE(平均绝对误差). 这里我们选择MSE进行评价。
epoch, 为每个批次数据的标记,等于i, 就是上面的epoch*step.
loss_log_df = pd.DataFrame(loss_log, columns=['epoch', 'MSE'])
epoch = loss_log_df['epoch']
MSE,就是loss
mse = loss_log_df['MSE']
测试集的MSE,
# 测试集结果
# normed_test_data, test_labels
out = model(normed_test_data.values)
test_mse = tf.reduce_mean(tf.losses.MSE(test_labels.values, out))
方式2
模型构建
network = Sequential([
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
network.build(input_shape=(None, 9))
network.summary()
network.compile(
optimizer=keras.optimizers.RMSprop(0.001),
loss='mse',
metrics=['mse', 'mae']
)
EPOCH = 200
history = network.fit(
normed_train_data.values,
train_labels.values,
epochs=EPOCH,
validation_split=0.2
)
参数查看
这里用的指标是MSE.
测试集的最终结果,为一个点结果:
out = network.predict(normed_test_data.values)
test_mse = tf.reduce_mean(tf.losses.MSE(test_labels.values, out))
训练的中间结果,在history.history中,
history.history.keys()
dict_keys(['loss', 'mse', 'mae', 'val_loss', 'val_mse', 'val_mae'])
训练误差,和验证集误差如下:
mse = history.history['mse']
val_mse = history.history['val_mse']
epoch = range(EPOCH)
作图
方式1-结果
查看结果
loss_log_df.plot.line(
x='epoch',
y='MSE'
)
如图3,最终训练集MSE为2.66,测试集结果为6.33.
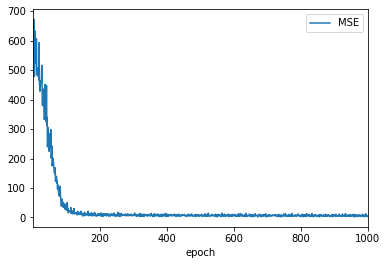
图3 每组数据的MSE
方式2-结果
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['KaiTi']
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
plt.plot(epoch, mse, 'r', label='train mse')
plt.plot(epoch, val_mse, 'b', label='validate mse')
plt.plot(EPOCH, float(test_mse), 'go', label='test mse')
plt.title('训练集和验证集的MSE,测试集的最终MSE')
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.legend()
如图4,最终训练集MSE为2.82,验证集MSE为7.50,测试集MSE为7.60.
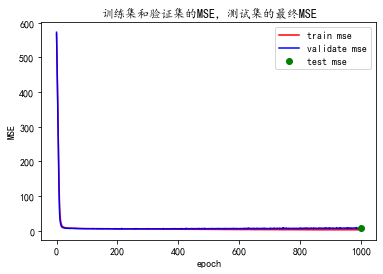
图4 训练集和验证集的MSE,测试集的最终MSE
from sklearn.metrics import r2_score
out_r2 = r2_score(out, test_labels.values)
print(out_r2)
直接的MSE需要对数据比较了解,才能看出模型的好坏,不是很直观。R2 Score就比较直观了,越接近1表示模型越好。该模型在测试集上的R2 Score为0.88.
结论
通过全连接神经网络来做汽车的效能指标MPG的回归预测。主要建模过程,包括数据加载、数据处理、数据观察、创建模型。创建模型包括模型选择、模型训练、模型评估。
该问题很明确,是一个回归问题,业务明确。而且已经选择好了模型。通过作图一节,直观看到模型训练过程,得到评价指标,包括MSE, R2 score等。最终得到的R2 score为0.88.
全连接神经网络是最基础神经网络模型。一般认为神经网络是端到端的一类模型,不需要做特征过程。这个是在图像、音频方面,神经网络会自动提取特征。但是在处理一些问题中,做一些特征过程,可以使模型训练更快、降低模型复杂度。
参考
1.TensorFlow深度学习,https://github.com/dragen1860/Deep-Learning-with-TensorFlow-book ,2019



