伸展树的实现——c++
一、介绍
伸展树(Splay Tree)是一种二叉排序树,它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。
(01) 伸展树属于二叉查找树,即它具有和二叉查找树一样的性质:假设x为树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。
(02) 除了拥有二叉查找树的性质之外,伸展树还具有的一个特点是:当某个节点被访问时,伸展树会通过旋转使该节点成为树根。这样做的好处是,下次要访问该节点时,能够迅速的访问到该节点。
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生,它是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
相比于"二叉查找树"和"AVL树",学习伸展树时需要重点关注是"伸展树的旋转算法"。
二、伸展树的c++实现
1. 基本定义
1.1 节点
template <class T> class SplayTreeNode{ public: T key; // 关键字(键值) SplayTreeNode *left; // 左孩子 SplayTreeNode *right; // 右孩子 SplayTreeNode():left(NULL),right(NULL) {} SplayTreeNode(T value, SplayTreeNode *l, SplayTreeNode *r): key(value), left(l),right(r) {} };
SplayTreeNode是伸展树节点对应的类。它包括的几个组成元素:
(01) key -- 是关键字,是用来对伸展树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
1.2 伸展树
template <class T> class SplayTree { private: SplayTreeNode<T> *mRoot; // 根结点 public: SplayTree(); ~SplayTree(); // 前序遍历"伸展树" void preOrder(); // 中序遍历"伸展树" void inOrder(); // 后序遍历"伸展树" void postOrder(); // (递归实现)查找"伸展树"中键值为key的节点 SplayTreeNode<T>* search(T key); // (非递归实现)查找"伸展树"中键值为key的节点 SplayTreeNode<T>* iterativeSearch(T key); // 查找最小结点:返回最小结点的键值。 T minimum(); // 查找最大结点:返回最大结点的键值。 T maximum(); // 旋转key对应的节点为根节点,并返回值为根节点。 void splay(T key); // 将结点(key为节点键值)插入到伸展树中 void insert(T key); // 删除结点(key为节点键值) void remove(T key); // 销毁伸展树 void destroy(); // 打印伸展树 void print(); private: // 前序遍历"伸展树" void preOrder(SplayTreeNode<T>* tree) const; // 中序遍历"伸展树" void inOrder(SplayTreeNode<T>* tree) const; // 后序遍历"伸展树" void postOrder(SplayTreeNode<T>* tree) const; // (递归实现)查找"伸展树x"中键值为key的节点 SplayTreeNode<T>* search(SplayTreeNode<T>* x, T key) const; // (非递归实现)查找"伸展树x"中键值为key的节点 SplayTreeNode<T>* iterativeSearch(SplayTreeNode<T>* x, T key) const; // 查找最小结点:返回tree为根结点的伸展树的最小结点。 SplayTreeNode<T>* minimum(SplayTreeNode<T>* tree); // 查找最大结点:返回tree为根结点的伸展树的最大结点。 SplayTreeNode<T>* maximum(SplayTreeNode<T>* tree); // 旋转key对应的节点为根节点,并返回值为根节点。 SplayTreeNode<T>* splay(SplayTreeNode<T>* tree, T key); // 将结点(z)插入到伸展树(tree)中 SplayTreeNode<T>* insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z); // 删除伸展树(tree)中的结点(键值为key),并返回被删除的结点 SplayTreeNode<T>* remove(SplayTreeNode<T>* &tree, T key); // 销毁伸展树 void destroy(SplayTreeNode<T>* &tree); // 打印伸展树 void print(SplayTreeNode<T>* tree, T key, int direction); };
playTree是伸展树对应的类。它包括根节点mRoot和伸展树的函数接口。
2. 旋转(重点)
/* * 旋转key对应的节点为根节点,并返回值为根节点。 * * 注意: * (a):伸展树中存在"键值为key的节点"。 * 将"键值为key的节点"旋转为根节点。 * (b):伸展树中不存在"键值为key的节点",并且key < tree->key。 * b-1 "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。 * b-2 "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。 * (c):伸展树中不存在"键值为key的节点",并且key > tree->key。 * c-1 "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。 * c-2 "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。 */ template <class T> SplayTreeNode<T>* SplayTree<T>::splay(SplayTreeNode<T>* tree, T key) { SplayTreeNode<T> N, *l, *r, *c; if (tree == NULL) return tree; N.left = N.right = NULL; l = r = &N; for (;;) { if (key < tree->key) { if (tree->left == NULL) break; if (key < tree->left->key) { c = tree->left; /* rotate right */ tree->left = c->right; c->right = tree; tree = c; if (tree->left == NULL) break; } r->left = tree; /* link right */ r = tree; tree = tree->left; } else if (key > tree->key) { if (tree->right == NULL) break; if (key > tree->right->key) { c = tree->right; /* rotate left */ tree->right = c->left; c->left = tree; tree = c; if (tree->right == NULL) break; } l->right = tree; /* link left */ l = tree; tree = tree->right; } else { break; } } l->right = tree->left; /* assemble */ r->left = tree->right; tree->left = N.right; tree->right = N.left; return tree; } template <class T> void SplayTree<T>::splay(T key) { mRoot = splay(mRoot, key); }
上面的代码的作用:将"键值为key的节点"旋转为根节点,并返回根节点。它的处理情况共包括:
(a):伸展树中存在"键值为key的节点"。
将"键值为key的节点"旋转为根节点。
(b):伸展树中不存在"键值为key的节点",并且key < tree->key。
b-1) "键值为key的节点"的前驱节点存在的话,将"键值为key的节点"的前驱节点旋转为根节点。
b-2) "键值为key的节点"的前驱节点存在的话,则意味着,key比树中任何键值都小,那么此时,将最小节点旋转为根节点。
(c):伸展树中不存在"键值为key的节点",并且key > tree->key。
c-1) "键值为key的节点"的后继节点存在的话,将"键值为key的节点"的后继节点旋转为根节点。
c-2) "键值为key的节点"的后继节点不存在的话,则意味着,key比树中任何键值都大,那么此时,将最大节点旋转为根节点。
下面列举个例子分别对a进行说明。
在下面的伸展树中查找10,共包括"右旋" --> "右链接" --> "组合"这3步。
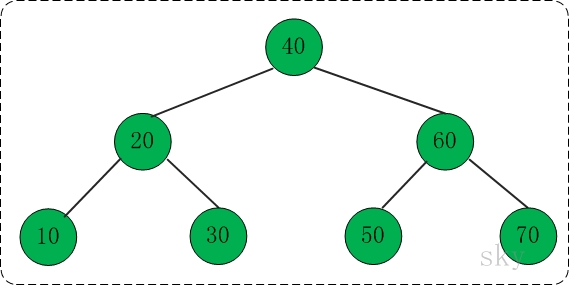
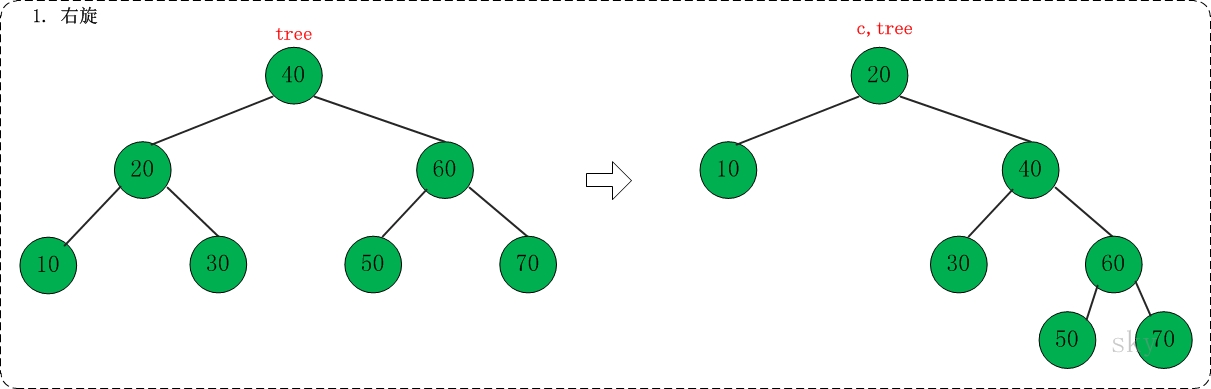
(01) 右旋
对应代码中的"rotate right"部分
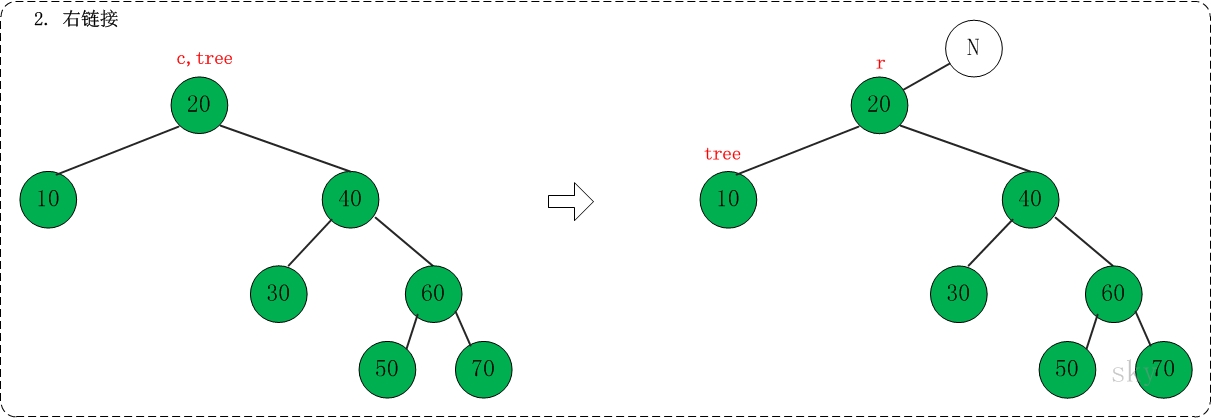
(02) 右链接
对应代码中的"link right"部分
(03) 组合
对应代码中的"assemble"部分
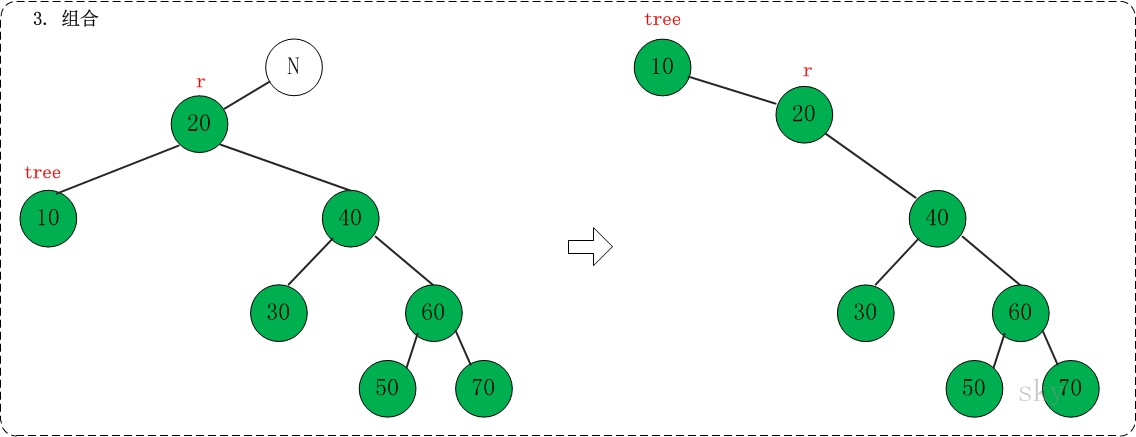
提示:如果在上面的伸展树中查找"70",则正好与"示例1"对称,而对应的操作则分别是"rotate left", "link left"和"assemble"。
其它的情况,例如"查找15是b-1的情况,查找5是b-2的情况"等等,这些都比较简单,大家可以自己分析。
3. 插入节点
/* * 将结点插入到伸展树中,并返回根节点 * * 参数说明: * tree 伸展树的根结点 * key 插入的结点的键值 * 返回值: * 根节点 */ template <class T> SplayTreeNode<T>* SplayTree<T>::insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z) { SplayTreeNode<T> *y = NULL; SplayTreeNode<T> *x = tree; // 查找z的插入位置 while (x != NULL) { y = x; if (z->key < x->key) x = x->left; else if (z->key > x->key) x = x->right; else { cout << "不允许插入相同节点(" << z->key << ")!" << endl; delete z; return tree; } } if (y==NULL) tree = z; else if (z->key < y->key) y->left = z; else y->right = z; return tree; } template <class T> void SplayTree<T>::insert(T key) { SplayTreeNode<T> *z=NULL; // 如果新建结点失败,则返回。 if ((z=new SplayTreeNode<T>(key,NULL,NULL)) == NULL) return ; // 插入节点 mRoot = insert(mRoot, z); // 将节点(key)旋转为根节点 mRoot = splay(mRoot, key); }
4. 删除节点
/* * 删除结点(节点的键值为key),返回根节点 * * 参数说明: * tree 伸展树的根结点 * key 待删除结点的键值 * 返回值: * 根节点 */ template <class T> SplayTreeNode<T>* SplayTree<T>::remove(SplayTreeNode<T>* &tree, T key) { SplayTreeNode<T> *x; if (tree == NULL) return NULL; // 查找键值为key的节点,找不到的话直接返回。 if (search(tree, key) == NULL) return tree; // 将key对应的节点旋转为根节点。 tree = splay(tree, key); if (tree->left != NULL) { // 将"tree的前驱节点"旋转为根节点 x = splay(tree->left, key); // 移除tree节点 x->right = tree->right; } else x = tree->right; delete tree; return x; } template <class T> void SplayTree<T>::remove(T key) { mRoot = remove(mRoot, key); }
remove(key)是外部接口,remove(tree, key)是内部接口。
remove(tree, key)的作用是:删除伸展树中键值为key的节点。
它会先在伸展树中查找键值为key的节点。若没有找到的话,则直接返回。若找到的话,则将该节点旋转为根节点,然后再删除该节点。
本文来自http://www.cnblogs.com/skywang12345/p/3604238.html





 浙公网安备 33010602011771号
浙公网安备 33010602011771号