泰勒公式和麦克劳林公式
Taylor formula(泰勒级数)用一个函数在某一点的连续导数之和来表示这个函数。如果函数在在点x=x0处有n阶导数,则f(x)可以按以下式子展开:
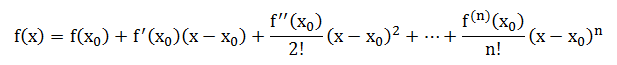
其目的在于用多项式函数逼近函数。如果x0=0,就是Maclaurin formula(麦克劳林公式):

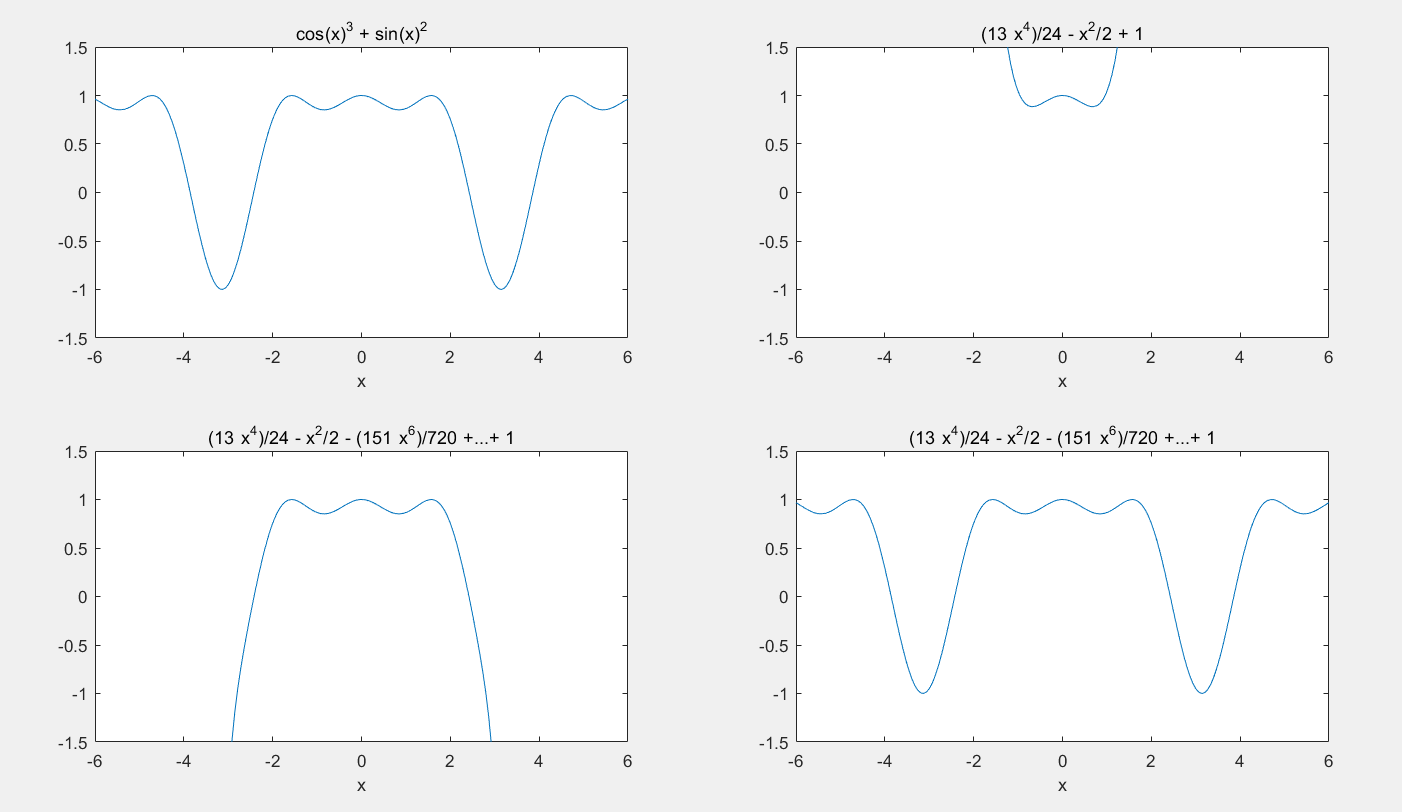
n的值越大,越逼近f(x),下图是f(x)=sin2x+cos3x在x0=0处的5阶、20阶和50阶展开,可见n的值越大,和f(x)越逼近。
Taylor formula(泰勒级数)用一个函数在某一点的连续导数之和来表示这个函数。如果函数在在点x=x0处有n阶导数,则f(x)可以按以下式子展开:
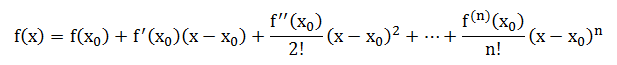
其目的在于用多项式函数逼近函数。如果x0=0,就是Maclaurin formula(麦克劳林公式):

n的值越大,越逼近f(x),下图是f(x)=sin2x+cos3x在x0=0处的5阶、20阶和50阶展开,可见n的值越大,和f(x)越逼近。

