超参数贝叶斯优化

超参数(Hyper-parameter)是定义模型或者定义训练过程的参数,是相对于模型参数(Parameter)来说的,比如目标检测网络的网络结构,激活函数的选择,学习率的大小,Anchor的尺寸等等,都属于超参数.超参数对网络的性能(如目标检测网络的mAP等)有很大的影响,因此需要找到性能最优的参数组合,也就是超参数优化(Hyper-parameter Optimization,HPO),通俗的说就是调参.

调参有很多方法,比如说网格搜索(Grid Search, GS)、随机搜索(Random Search, RS),各种进化计算算法,如遗传算法(Genetic Algorithm, GA)、粒子群优化(Paticle Swarm Optimization, PSO)等等,但是这些方法都不适用于超参数优化,因为超参数评估一个参数组合的性能,需要用这个参数组合训练神经网络,再评估网络的性能,而训练神经网络计算量很大,需要很长的时间,因此评估的参数组合的数量不能太多,只能评估少数的参数组合的性能.最适合的方法就是贝叶斯优化(Bayesian Optimization)了.

贝叶斯优化只需要几个参数组合以及它们的性能,再进行高斯过程回归(Gaussian Process Regression, GPR),然后就可以计算出很多参数组合取值点的期望值和方差,期望值表明这个点最优可能的性能,方差表明这个点性能的不确定性.

如上图所示,用4个点的值进行高斯过程回归,然后可以计算出很多点的期望值和方差,有的点期望值高,有的点方差大,到底选择哪些点,就涉及到开发(exploritation)和探索(exploration)均衡的问题了.期望值高的点是我们需要的,但是方差大的点也是需要的,因为方差大的点虽然期望值不是很高,但是不确定性较大,有可能出现更高的值.究竟选哪些点,就要用到采集函数(Acquisition Function)了,最简单的采集函数是期望值加上方差的n倍(n可以是整数、小数、正数、负数).如下图所示,选择采集函数最大的点.

根据选择的点的参数组合,又进行一次模型训练,再评估模型的性能,这样就有了5个点的值,于是又可以进行一次高斯过程回归,选择采集函数最大的点,再训练模型和评估,得到第6个点的值,如下图所示.

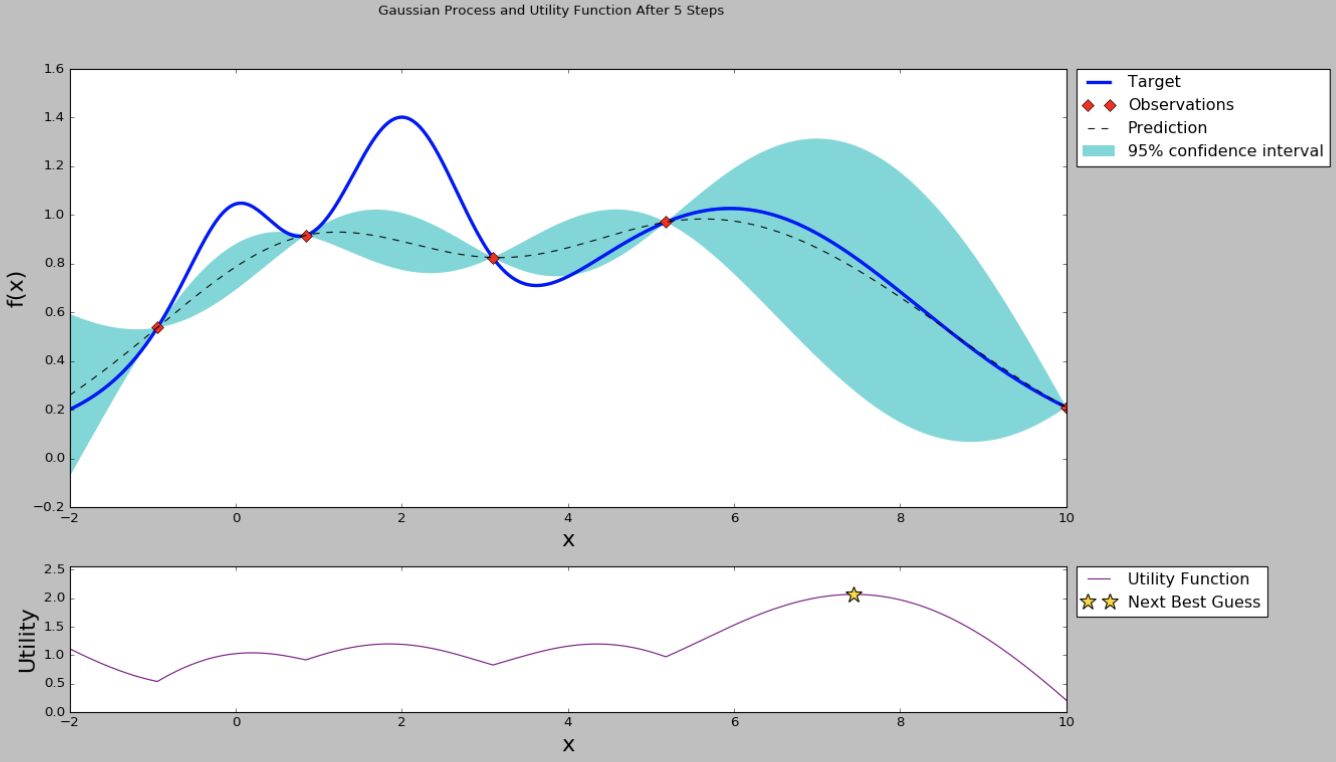
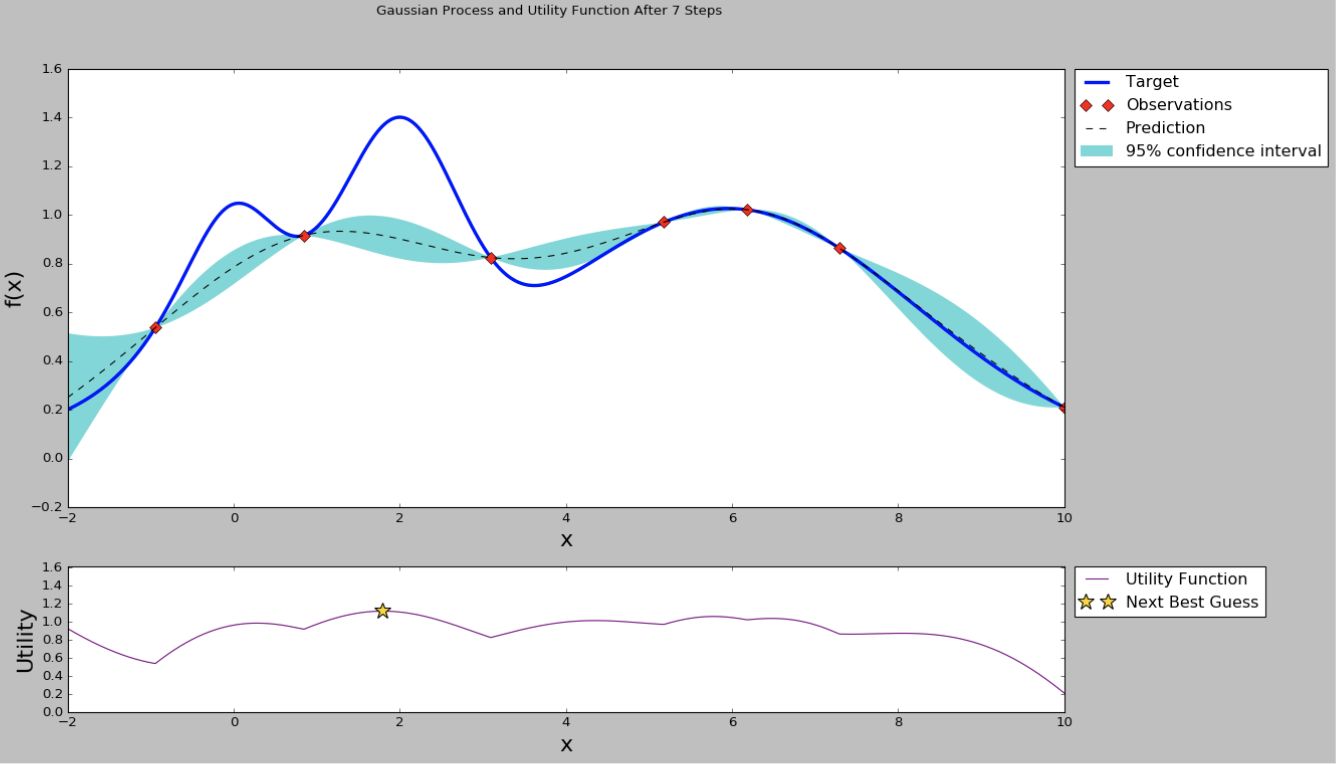
以上过程反复进行,通过计算有限的点的性能,可以使曲线逐渐逼近真实曲线,从而可以选择性能最优,或者说接近最优的超参数组合,取得不错的模型性能.