完全背包问题

在学习完全背包前我们要先学习一下01背包01背包

完全背包

注意：

01背包的转移方程为

• 

完全背包的状转移方程为

• f[i][j] = max(f[i - 1][j]  ,  f[i - 1][j - v] + w  ,  f[i - 1][j - 2 * v] + 2 * w  ,  f[i - 1][j - 3 * v] + 3 * w , .....)
  f[i][j - v] = max(f[i - 1][j - v],f[i - 1][j - 2 * v] + w,f[i - 1][j - 3 * v] + 2 * w  ,  f[i - 1][j - 4 * v] + 3 * w , .....)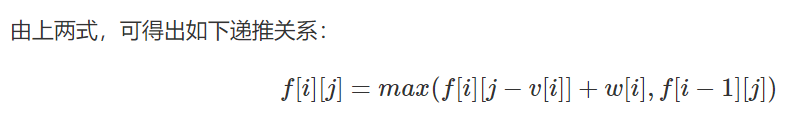

• 

 

 

题目AC代码：

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N = 1010;
int v[N], w[N];
int dp[N];
int n, V;

signed main()
{
    cin >> n >> V;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 0; j <= V; j ++)
        {
            if(j >= v[i]) dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    
    cout << dp[V] << endl;
   
    return 0;
   
}