组合数问题

题目链接

组合数：

组合数​表示的是从n个物品中选出m个物品的方案数。举个例子,从$(1,2,3)$三个物品中选择两个物品可以有$(1,2),(1,3),(2,3)$这三种选择方法。 根据组合数的定义，我们可以给出计算组合数的一般公式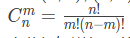：其中n!=1×2×⋯×n。特别地，定义0!=1。

公式：

最后一个公式还可以表示：

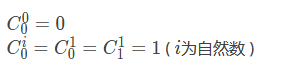
这是什么？是不是像杨辉三角？没错，这就是杨辉三角的定义。这个三角可以解决很多问题，记住打印三角的方法也可以打出组合数。

代码：

const int N = 2e3 + 10;
int f[N][N];
int ans[N][N];

void InitAns(int k) {
	f[0][0] = f[1][0] = f[1][1] = 1;
	for (int i = 2; i <= 2000; i ++) {
		f[i][0] = 1                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                               ;
		for (int j = 1; j <= i; j ++) { //组合数其实是与杨辉三角联系在一起的，之前竟然不知道oo。
			f[i][j] = (f[i - 1][j - 1] % k + f[i - 1][j] % k) % k;
			ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1];
			if (!f[i][j]) ans[i][j]++;
		}
		ans[i][i + 1] = ans[i][i]; //这行主要是对ans的下一行求最后一个f[i][i]的时候用的，万万不可省略！！！
	}
}

AC代码：

#include<iostream>

using namespace std;

const int N = 2e3 + 10;
int f[N][N];
int ans[N][N];

void InitAns(int k) {
	f[0][0] = f[1][0] = f[1][1] = 1;
	for (int i = 2; i <= 2000; i ++) {
		f[i][0] = 1                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                               ;
		for (int j = 1; j <= i; j ++) { //组合数其实是与杨辉三角联系在一起的，之前竟然不知道oo。
			f[i][j] = (f[i - 1][j - 1] % k + f[i - 1][j] % k) % k;
			ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1];
			if (!f[i][j]) ans[i][j]++;
		}
		ans[i][i + 1] = ans[i][i]; //这行主要是对ans的下一行求最后一个f[i][i]的时候用的，万万不可省略！！！
	}
}
int main() {
	int t, k;
	cin >> t >> k;
	InitAns(k);
	while (t--) {
		int x, y;
		cin >> x >> y;
		if (x >= y)
			cout << ans[x][y] << endl;
		else cout << ans[x][x] << endl;

	}


	return 0;
}