ST算法详解

 ST算法

st算法是用来求解区间最大值的一种方式，他相比朴树算法他的效率更高，为nlog(n)。

st算法的学习过程：

很幸运途中有艺颖学姐的讲解，虽然当时没有听懂，但是帮助还是挺大的。可以说这个知识的学习用的时间比较多，但是他是一个开始。在艺颖学姐的引导下我决定要写我的博客了，我感觉还挺好的，记录自己的学习嘛。

st正文开始

st的思想是倍增的思想，他将一个n^2的复杂公式优化为了nlog(n)。

　每一区间段都可以用两个区间表示（一个数的情况除外）。我们构建dp[i][j]数组，其含义如下：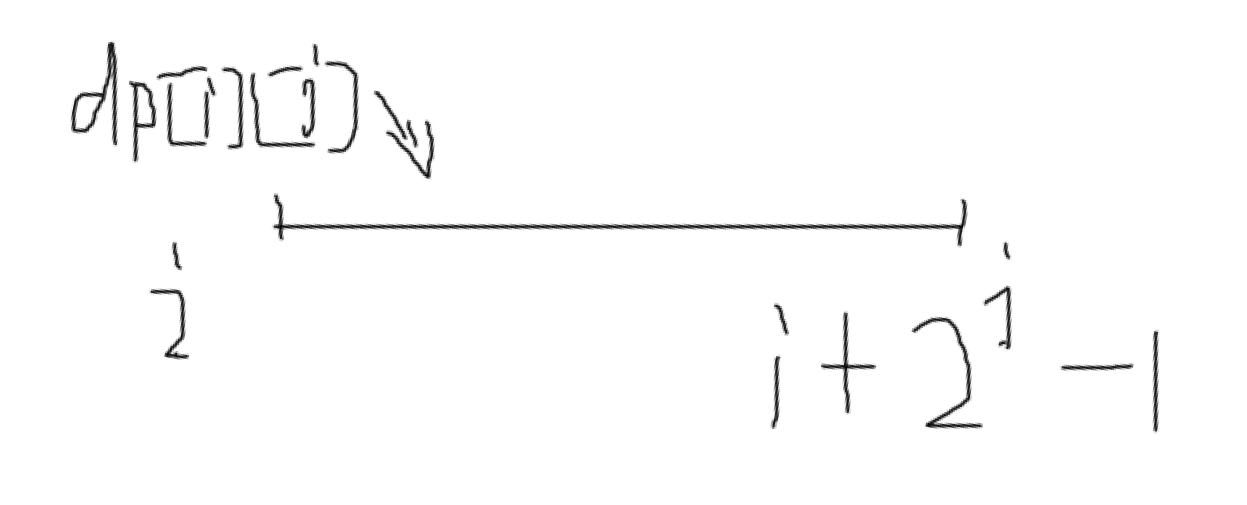

 

 

我们首先处理dp数组

边界条件就是dp[i][0]表示a[i]本身。

for(int i = 1; i <= n; i ++) dp[i][0] = a[i];

然后进行求k, k相当于区间右边界，因为log2(n)取int默认向下取整，所以不会出现右边界大于从1开始右边界就大于n的情况

 int k; 2 k = (int)log2(n); //（int）log2(n)是向下取整，所以不会超过数组个数 

最后就是循环求解dp了，个人觉得最难的地方在理解 i 和 j。反正是困扰我了好几天。看代码：

for(int j = 1; j <= k; j ++)  //j 是枚举的右端点
    {
        for(int i = 1; i + (1 << j) - 1<= n; i ++) //因为我们是以jdp[i][j]，所以要满足i + (1 << j) - 1<= n
        {
            // dp[i][j] = min(dp[i][j-1], dp[i + (1 << (j - 1))][j - 1]) #求最小值
            dp[i][j] = max(dp[i][j-1], dp[i + (1 << (j - 1))][j - 1]) ;//我们在求j的时候实际上是运用j-1进行求解的
        }
    }

附上本函数的全部代码：

void st_prework(vector<int> a, int n) 
{
    for(int i = 1; i <= n; i ++) dp[i][0] = a[i];
    int k;
    k = (int)log2(n); //（int）log2(n)是向下取整，所以不会超过数组个数

    for(int j = 1; j <= k; j ++)  //j 是枚举的右端点
    {
        for(int i = 1; i + (1 << j) - 1<= n; i ++) //因为我们是以jdp[i][j]，所以要满足i + (1 << j) - 1<= n
        {
            // dp[i][j] = min(dp[i][j-1], dp[i + (1 << (j - 1))][j - 1]) #求最小值
            dp[i][j] = max(dp[i][j-1], dp[i + (1 << (j - 1))][j - 1]) ;//我们在求j的时候实际上是运用j-1进行求解的
        }
    }
}

查询操作，时间复杂度度为O(1)

一个区间总能划分为两个区间（1个数除外），下面我们看图

 

 

 

 

 

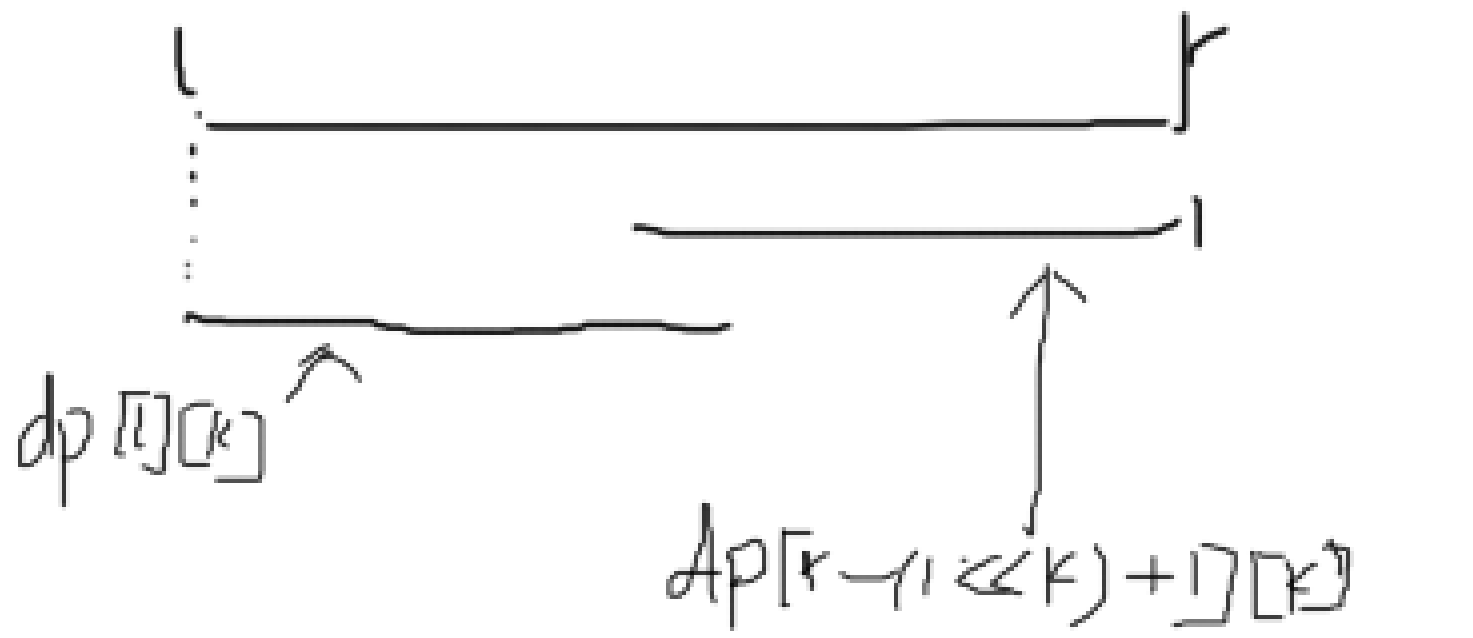
 k 表示的是区间的大小：

1 int k;
k = (int)log2(r - l + 1); //k表示的是l后有2^k个数，因为该函数默认向下取整, 所以 l + 2^k - 1不会大于 r;

那我们直接返回就行了。

 return max(dp[l][k], dp[r - (1 << k) + 1][k]); // 为什么i是(r - (1 << k) + 1),因为 l + 2^k - 1一定 <= r,而(r - (1 << k) + 1) >= l, 且(r - (1 << k) + 1) + 2^k = dp[r][1],为查询区间的末尾

最后附上该函数全部代码：

int st_query(int l, int r)
{
    int k;
    k = (int)log2(r - l + 1); //k表示的是l后有2^k个数，因为该函数默认向下取整, 所以 l + 2^k - 1不会大于 r;
    // return min(dp[l][k], dp[r - (1 << k) + 1][k]); #求最小的
    return max(dp[l][k], dp[r - (1 << k) + 1][k]); // 为什么i是(r - (1 << k) + 1),因为 l + 2^k - 1一定 <= r,而(r - (1 << k) + 1) >= l, 且(r - (1 << k) + 1) + 2^k = dp[r][1],为查询区间的末尾
}

全部代码如下：

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;
int n; //数组个数
int dp[N][32]; //dp数组，用于存储预处理将结果。dp[i][j],i表示的是数组的左边界，j表示的是左边界右边的2^j个的个数，包括i

void st_prework(vector<int> , int ); //预处理函数，使用倍增思想，以2^i为断点
int st_query(int l, int r); //在O(1)的时间里进行查询区间最值
int main() 
{
    cin >> n;
    vector<int>a (n + 1, 0); //定义一个有n + 1 个存储单元的容器
    for(int i = 1; i <= n; i ++) cin >> a[i];

    st_prework(a, n);
    int l, r;
    while(cin >> l >> r) 
    {
        cout << st_query(l, r) << endl;
    }



    return 0;
}

void st_prework(vector<int> a, int n) 
{
    for(int i = 1; i <= n; i ++) dp[i][0] = a[i];
    int k;
    k = (int)log2(n); //（int）log2(n)是向下取整，所以不会超过数组个数

    for(int j = 1; j <= k; j ++)  //j 是枚举的右端点
    {
        for(int i = 1; i + (1 << j) - 1<= n; i ++) //因为我们是以jdp[i][j]，所以要满足i + (1 << j) - 1<= n
        {
            // dp[i][j] = min(dp[i][j-1], dp[i + (1 << (j - 1))][j - 1]) #求最小值
            dp[i][j] = max(dp[i][j-1], dp[i + (1 << (j - 1))][j - 1]) ;//我们在求j的时候实际上是运用j-1进行求解的
        }
    }
}

int st_query(int l, int r)
{
    int k;
    k = (int)log2(r - l + 1); //k表示的是l后有2^k个数，因为该函数默认向下取整, 所以 l + 2^k - 1不会大于 r;
    // return min(dp[l][k], dp[r - (1 << k) + 1][k]); #求最小的
    return max(dp[l][k], dp[r - (1 << k) + 1][k]); // 为什么i是(r - (1 << k) + 1),因为 l + 2^k - 1一定 <= r,而(r - (1 << k) + 1) >= l, 且(r - (1 << k) + 1) + 2^k = dp[r][1],为查询区间的末尾
}

 

 

最后感谢你的观看，如果有问题请直接指出，谢谢。