Odds calculation required for the python strategy library

Bet Class

class strats.Bet(inp)[source]

Here is an example of the expected string input on instantiation of the class. It is expecting a string using the POST method in a cgi script receiving a textarea input from an HTML form.

As one can see, the expected text that looks like Python code. This means that these variables can be immediately “compiled” into the code for the class upon instantiation. This is an example of a string for betting on the trifecta that is passed to the class instantiation code, __init__().

self.bet_type = "Trifecta"
self.nraces = 1
self.horse_ids.append([1,2,4,5,6,8,9])
self.user_odds.append([2.0,4.2,4.2,5.5,5.9,9.4,11.0])
self.tab_odds.append([3.9,7.2,4.2,5.5,5.9,9.4,11.0])
self.jockeys.append([1,2,3,4,5,6,7])
self.trainers.append([1,2,3,4,5,6,7])
self.standouts_1.append([1,2])
self.standouts_2.append([1,2,4,5])
self.standouts_3.append([])
self.value = True
self.scale_var = 100
user_div_range = (0,750)
tab_div_range = (750,5000)

Note

• I think there needs to be some variables to describe what to do with the jockey and trainer info?
• I don’t understand max_tab_market_odds well enough to code it.
• Do we need the client’s ID?
• Do we need the Race ID?
• I think we will need to establish an order in which the rules are applied.
• Do we need to specify the stake for flat staking?
• Is there some kind of incosistency between enforcing total outlay as a restriction and the staking rules including round the rounding rules?

__init__(inp)[source]

Parameters:	inp (string) – user input as string probably from digesting a cgi transmission of a textarea html form element
Returns:	None

__module__ = 'strats'

bet_type = None

One of Quinella, Exacta, Trifecta, Pick 4, Pick 6, Quaddy, Superfecta

error_message(msg)[source]

This routine sends a error_message to the user. (usually because there is something wrong with the input.)

Return type:	None
Parameters:	msg – error_message string
Returns:	nil

fifth = []

fifth place standouts (after [] substitution)

find_common_combinations_and_sort(tabres, userres)[source]

Due to restrictions on win price lines and trifecta probabilities is is possible for the tab and user lists of probabilites mto not have the same combinations. This routine finds the common combinations and applies the overlay if specified.

Parameters:	tabres – list of tuples of (combinations,tab probabilities) userres –
Returns:	list of tuples containing (combination, tab probability, user probability)

first = []

first place standouts (after [] substitution)

flat_stakes = True

Flat stakes flag, if True, must define stake

fourth = []

fourth place standouts (after [] substitution)

get_multi_tab_restricted_ids(p, w, n)[source]

This routine restricts a price line according to

Return type:	list of ints
Parameters:	p – user or tab probability from win price line w – one of [tabodds1, tabodds2, ..., userodds1, userodds2,...] odds limits for price line and position n – for nth race
Returns:	tab ids consistent with odds restrictions

get_tab_restricted_ids(p, w)[source]

This routine restricts a price line according to

Parameters:	p – user or tab probability from win price line w – one of [tabodds1, tabodds2, ..., userodds1, userodds2,...] odds limits for price line and position
Returns:	tab ids consistent with odds restrictions

handle_both_price_lines(tabres, userres)[source]

Once the combination probabilities are calculated (including standouts and odds restrctions), this routine applies all of the other rules for betting if both tab and user price lines are provided. The logic is

• convert (id,prob) tuples into dictionaries
• find common TAB ids (odds restrictions enforce this)
• restrict combinations for overlay if required
• restrict combination by % number, % value, or total stake
• calculate staking for each combination according to flat_staking flag and rounding option
• print results

Parameters:	tabres – list of tuples (combinations, tab probabilities) userres – list of tuples (combinations, user probabilities)
Returns:	None
Return type:	None

handle_exacta()[source]

This routine handles the details of impmenting the rules when betting on the exacta.

Return type:	None
Returns:	number of bets, outlay, list of combinations

handle_pick4()[source]

This routine handles the details of impmenting the rules when betting on the pick 4 pools.

Return type:	None
Returns:	number of bets, outlay, list of combinations

handle_pick6()[source]

This routine handles the details of impmenting the rules when betting on the pick 6 pools.

Return type:	None
Returns:	number of bets, outlay, list of combinations

handle_quaddie()[source]

This routine handles the details of impmenting the rules when betting on the pick 4 pools.

Return type:	None
Returns:	number of bets, outlay, list of combinations

handle_quinella()[source]

This routine handles the details of impmenting the rules when betting on the exacta.

Return type:	None
Returns:	number of bets, outlay, list of combinations

handle_single_price_line(singleres)[source]

Once the combination probabilities are calculated (including standouts and odds restrctions), this routine applies all of the other rules for betting if both tab and user price lines are provided. The logic is

• restrict combination by % number, % value, or total stake
• calculate staking for each combination according to flat_staking flag and rounding option
• print results

Parameters:	singleres – list of tuples (combinations, tab or user probabilities)
Returns:	None
Return type:	None

handle_superfecta()[source]

This routine handles the details of impmenting the rules when betting on tsuperfecta.

Return type:	None
Returns:	number of bets, outlay, list of combinations

handle_trifecta()[source]

This routine handles the details of impmenting the rules when betting on the trifecta.

Return type:	None
Returns:	number of bets, outlay, list of combinations

horse_ids = []

list of lists of TAB ids for horses (one list for each race)

jockey_list = []

list of lists of jockeys (one for each race) This parameter is only for multiple race bets.

max_tab_market_odds = (0, 0)

I don’t know how to define this. Currently unimplemented

multi_race_preprocess(nraces)[source]

This routine handles the preprocessing for multiple race betting pools:

• nraces needs to be 1
• at least one of user odds or TAB odds must be provided
• ensure that odds are only for one race
• list of horse TAB ids must be provided and be of same length as odds provided
• check to make sure jockey and trainer info not provided

Process input in the following order

• remove scratchings, taking care to delete runner info from end of the appropriate lists
• scale TAB and/or user odds
• process standouts

Parameters:	nraces (int) – number of races for pool
Returns:	Flag for tab divs, flag for user divs, tab prob list, user prob list

multi_race_scale_odds(ntabodds, nuserodds)[source]

This routine scales the odds and calculates the relevant probability of the user and/or tab win price line.

Parameters:	ntabodds – 1 if have tab odds, 0 otherwise nuserodds – 1 if have user odds, 0 otherwise
Returns:	tab prob list, user prob list

multi_race_scratchings(ntabodds, nuserodds)[source]

Parameters:	ntabodds – 1 if tab odds present, 0 otherwise nuserodds – 1 if user odds present, 0 otherwise
Returns:	None

multi_race_validation(nraces)[source]

This routine checks for a number of possible input errors for a single race pool.

Returns:

nraces = 0

number of races for which data is input

outlay_amount = 10000000.0

cap on outlay be in order of probability

overlay = False

True if value betting; else False

overlay_scale = 1.0

If value betting, bet if (user_div * overlay_scale) <= tab_div

percent_by_number = 0

Top percent of bets by number accepted after all other conditions applied if 100, accept all, if <= 0 dont’t calculate

percent_by_value = 0

Top percent of bets by value accepted after all other conditions applied if 100, accept all, , if <= 0, don’t calculate

prob_exacta(prob, s1, s2, sort=False)[source]

This routine calculates the normalized exacta probabilites given an input list of horse ids and normalized win probabilities.

If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (first) and jj (second) as the winning combination is given by

 

 

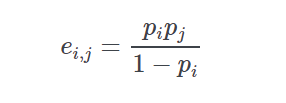
Return type:	list
Parameters:	prob – list of tuples of form (id,win probability) s1 – list of allowed first place ids defined by odds range s2 – list of allowed second place ids defined by odds range sort – Boolean if True, result is sorted, highest probability first
Returns:	list of tuples of form ((id1,id2),exacta_probability)

So if we input prob as:

(1, 0.15557814847495188)
(2, 0.20438859122263553)
(3, 0.3708534602327072)
(4, 0.19948464099114765)
(5, 0.034061786039927267)
(6, 0.021204203862783776)
(7, 0.0031196067348740163)
(8, 0.01130956244097265)

The first few exacta probabilities (if unsorted) would be:

(1, 2) 0.0476639105054
(1, 3) 0.117045542403
(1, 4) 0.0461010957068
(1, 5) 0.00569989602184
(1, 6) 0.00345321559886
(1, 7) 0.000488654491335
(1, 8) 0.0018032135443

If sorted, the first few exacta probabilities would be:

(3, 2) 0.12047784021
(3, 4) 0.11758718311
(2, 3) 0.0952703989043
(4, 3) 0.0924149281363
(3, 1) 0.0917062894757
(1, 3) 0.0683268612653
(2, 4) 0.0512466064374

prob_pick4(prob, s1, s2, s3, s4, sort=False)[source]

This routine calculates the normalized first four probabilites given an input list of horse ids and normalized win probabilities.

If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (first), jj (second), kk (third), and ll (fourth)as the winning combination is given by

 

 

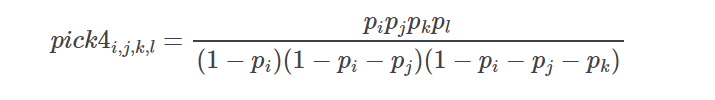
Return type:	list
Parameters:	prob – list of tuples of form (id,win probability) s1 – list of allowed first place ids defined by odds range s2 – list of allowed second place ids defined by odds range s3 – list of allowed third place ids defined by odds range s4 – list of allowed fourth place ids defined by odds range sort – Boolean if True, result is sorted, highest probability first
Returns:	list of tuples of form ((id1,id2,id3,id4),pick 4 probability)

So if we input prob as:

(1, 0.15557814847495188)
(2, 0.20438859122263553)
(3, 0.3708534602327072)
(4, 0.19948464099114765)
(5, 0.034061786039927267)
(6, 0.021204203862783776)
(7, 0.0031196067348740163)
(8, 0.01130956244097265)

The first few pick 4 probabilities (if unsorted) would be:

(1, 2, 3, 4) 0.0161700951381
(1, 2, 3, 5) 0.00276102620283
(1, 2, 3, 6) 0.00171879896159
(1, 2, 3, 7) 0.000252873291125
(1, 2, 3, 8) 0.000916745769159
(1, 2, 4, 3) 0.00988009673754
(1, 2, 4, 5) 0.000907457465589
(1, 2, 4, 6) 0.000564912041741
(1, 2, 4, 7) 8.3111038803e-05
(1, 2, 4, 8) 0.000301303838195

If sorted, the first few pick 4 probabilities would be:

(1, 2, 3, 4) 0.0161700951381
(1, 2, 3, 5) 0.00276102620283
(1, 2, 3, 6) 0.00171879896159
(1, 2, 3, 7) 0.000252873291125
(1, 2, 3, 8) 0.000916745769159
(1, 2, 4, 3) 0.00988009673754
(1, 2, 4, 5) 0.000907457465589
(1, 2, 4, 6) 0.000564912041741
(1, 2, 4, 7) 8.3111038803e-05
(1, 2, 4, 8) 0.000301303838195

prob_pick6(prob, s1, s2, s3, s4, s5, s6, sort=False)[source]

This routine calculates the normalized first six probabilites given an input list of horse ids and normalized win probabilities.

If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (first), jj (second), kk (third), :param s1: ll (fourth), mm (fifth), and nn (sixth) as the winning combination is given by

 

 

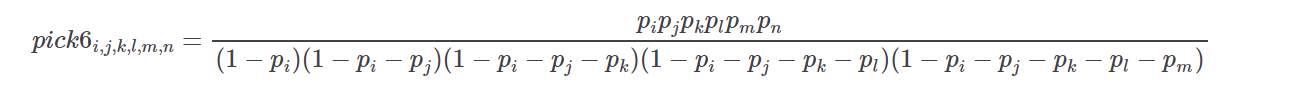
Return type:	list
Parameters:	prob – list of tuples of form (id,win probability) s1 – list of allowed first place ids defined by odds range s2 – list of allowed second place ids defined by odds range s3 – list of allowed third place ids defined by odds range s4 – list of allowed fourth place ids defined by odds range s5 – list of allowed fifth place ids defined by odds range s6 – list of allowed sixth place ids defined by odds range sort – Boolean if True, result is sorted, highest probability first
Returns:	list of tuples of form ((id1,id2,id3,id4,id5,id6),pick 6 probability)

So if we input prob as:

(1, 0.15557814847495188)
(2, 0.20438859122263553)
(3, 0.3708534602327072)
(4, 0.19948464099114765)
(5, 0.034061786039927267)
(6, 0.021204203862783776)
(7, 0.0031196067348740163)
(8, 0.01130956244097265)

The first few pick 6 probabilities (if unsorted) would be:

(1, 2, 3, 4, 5, 6) 0.00470264737409
(1, 2, 3, 4, 5, 7) 0.000691863298187
(1, 2, 3, 4, 5, 8) 0.00250822357959
(1, 2, 3, 4, 6, 5) 0.00345572050302
(1, 2, 3, 4, 6, 7) 0.000316498052757
(1, 2, 3, 4, 6, 8) 0.00114740568101
(1, 2, 3, 4, 7, 5) 0.000370307449629
(1, 2, 3, 4, 7, 6) 0.000230524454726

If sorted, the first few pick 6 probabilities would be:

(3, 2, 4, 1, 5, 6) 0.0113643296974
(3, 4, 2, 1, 5, 6) 0.0112346228107
(3, 2, 1, 4, 5, 6) 0.00951066959114
(3, 4, 1, 2, 5, 6) 0.0092338952488
(2, 3, 4, 1, 5, 6) 0.00898658393663
(4, 3, 2, 1, 5, 6) 0.00882959207139
(3, 1, 2, 4, 5, 6) 0.00853040992409
(3, 1, 4, 2, 5, 6) 0.00837778246743

Timings of routine with n sized fields

n	Unsorted (sec)	Sorted (sec)
6	0.002	0.004
8	0.037	0.128
10	0.247	1.12
12	1.10	5.60
14	3.95	23.8
16	13.1	97.2
18	62.3
20	Memory

prob_quaddie(ids, prob, s1, s2, s3, s4, sort=False)[source]

This routine calculates the quaddie probabilites given an input list of horse ids and normalized win probabilities for each of the four races

If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (in the first race), jj (in the second race), kk (in the third race), and ll (in the fourth race)as the winning combination is given by

 

 

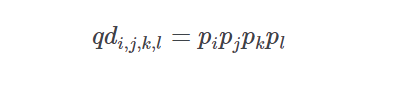
Parameters:	sort – if True sor by increasing probability ids – list of lists of TAB horse ids prob – list of lists of tuples of win probability) for each race s1 – list of horse ids to be considered for win in first race s2 – list of horse ids to be considered for win in second race s3 – list of horse ids to be considered for win in third race s4 – list of horse ids to be considered for win in fourth race
Return type:	list
Returns:	list of tuples of form ((id1,id2,id3,id4),quaddie probability)

So if we input the four race probabilities as:

 1 0.15558  1 0.86564  1 0.04397  1 0.76204
 2 0.20439  2 0.02050  2 0.04988  2 0.10846
 3 0.37085  3 0.02690  3 0.85491  3 0.08160
 4 0.19948  4 0.06478  4 0.04690  4 0.01898
 5 0.03406  5 0.01119  5 0.00072  5 0.01083
 6 0.02120  6 0.00605  6 0.00096  6 0.01692
 7 0.00312  7 0.00172  7 0.00267  7 0.00117
 8 0.00788  8 0.00068             8 0.00000
 9 0.00180  9 0.00230             9 0.00001
10 0.00068 10 0.00024            10 0.00000
11 0.00009                       11 0.00000
12 0.00087

The first few quaddie probabilities (if unsorted) would be:

(1, 1, 1, 1) 0.00451204255393
(1, 1, 1, 2) 0.000642180234069
(1, 1, 1, 3) 0.000483129743111
(1, 1, 1, 4) 0.000112363248935
(1, 1, 1, 5) 6.41234861406e-05
(1, 1, 1, 6) 0.000100176763996
(1, 1, 1, 7) 6.93229347721e-06
(1, 1, 1, 8) 1.50345086741e-08
(1, 1, 1, 9) 5.73763223463e-08

If sorted, the first few quaddie probabilities would be:

(3, 1, 3, 1) 0.2091383481
(2, 1, 3, 1) 0.115262487539
(4, 1, 3, 1) 0.112496963793
(1, 1, 3, 1) 0.0877364254662
(3, 1, 3, 2) 0.0297657904886
(3, 1, 3, 3) 0.0223936177872
(5, 1, 3, 1) 0.0192087345262
(2, 1, 3, 2) 0.0164048300393
(4, 1, 3, 2) 0.0160112245568
(3, 4, 3, 1) 0.0156519771072

Timings of routine with n sized fields for 4 races

n	Unsorted (sec)	Sorted (sec)
2	0	0
4	0	.003
6	.002	.007
8	.003	.018
10	.006	.049
12	.012	.109
14	.02	.215
16	.037	.40
18	.059	.648
20	.288	2.62

prob_quinella(prob, s1, s2, sort=False)[source]

This routine calculates the normalized quinella probabilites given an input list of horse ids and normalized win probabilities.

If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii and jj as the winning combination is given by

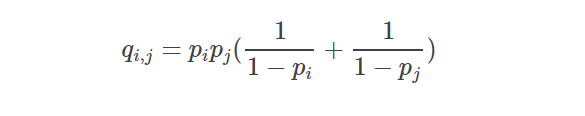
Return type:	list
Parameters:	prob – list of tuples of form (id,win probability) s1 – list of allowed first place ids defined by odds range s2 – list of allowed second place ids defined by odds range sort – Boolean if True, result is sorted, highest probability first
Returns:	list of tuples of form ((id1,id2),quinella_probability)

So if we input prob as:

(1, 0.15557814847495188)
(2, 0.20438859122263553)
(3, 0.3708534602327072)
(4, 0.19948464099114765)
(5, 0.034061786039927267)
(6, 0.021204203862783776)
(7, 0.0031196067348740163)
(8, 0.01130956244097265)

The first few quinella probabilities (if unsorted) would be:

(1, 0.15557814847495188)
(2, 0.20438859122263553)
(3, 0.3708534602327072)
(4, 0.19948464099114765)
(5, 0.034061786039927267)
(6, 0.021204203862783776)
(7, 0.0031196067348740163)
(8, 0.01130956244097265)

If sorted, the first few quinella probabilities would be:

(2, 3) 0.215748239115
(3, 4) 0.210002111247
(1, 3) 0.160033150741
(2, 4) 0.102179276603
(1, 2) 0.0776242539698
(1, 4) 0.0755228299148
(3, 5) 0.0331552537388
(3, 6) 0.0205329272655
(2, 5) 0.0159576376265

prob_superfecta(ids, prob, s1, s2, s3, s4, s5, s6, sort=False)[source]

This routine calculates the quaddie probabilites given an input list of horse ids and normalized win probabilities for each of the four races

If pp is the vector of normalized win probabilities derived from a price line then the probability of runner ii (in the first race), jj (in the second race), kk (in the third race), and ll (in the fourth race)as the winning combination is given by

 

 

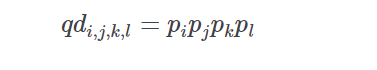
Parameters:	sort – if True sor by increasing probability ids – list of lists of TAB horse ids prob – list of lists of tuples of win probability) for each race s1 – list of horse ids to be considered for win in first race s2 – list of horse ids to be considered for win in second race s3 – list of horse ids to be considered for win in third race s4 – list of horse ids to be considered for win in fourth race s5 – list of horse ids to be considered for win in fifth race s6 – list of horse ids to be considered for win in sixth race
Return type:	list
Returns:	list of tuples of form ((id1,id2,id3,id4,id5,id6),quaddie probability)

prob_trifecta(prob, s1, s2, s3, sort=False)[source]

This routine calculates the trifecta probabilites given an input list of horse ids and normalized win probabilities.

If pp is the vector of win probabilities derived from a price line then the probability of runner ii (first), jj (second), and kk (third) as the winning combination is given by

 

 

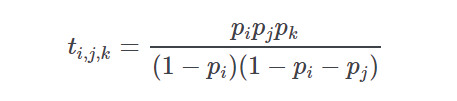
Return type:	list
Parameters:	prob – list of tuples of form (id,win probability) s1 – list of allowed first place ids defined by odds range s2 – list of allowed second place ids defined by odds range s3 – list of allowed third place ids defined by odds range sort – Boolean if True, result is sorted, highest probability first
Returns:	list of tuples of form ((id1,id2,id3),trifecta_probability)

So if we input prob as:

(1, 0.15557814847495188)
(2, 0.20438859122263553)
(3, 0.3708534602327072)
(4, 0.19948464099114765)
(5, 0.034061786039927267)
(6, 0.021204203862783776)
(7, 0.0031196067348740163)
(8, 0.01130956244097265)

The first few trifecta probabilities (if unsorted) would be:

(1, 2, 3) 0.0218195393628
(1, 2, 4) 0.0117368811219
(1, 2, 5) 0.0020040597189
(1, 2, 6) 0.00124757083445
(1, 2, 7) 0.000183545225398
(1, 2, 8) 0.000665409573642
(1, 3, 2) 0.0294893645215
(1, 3, 4) 0.0287818182974

If sorted, the first few trifecta probabilities would be:

(3, 2, 4) 0.0565815867228
(3, 4, 2) 0.0559357922362
(2, 3, 4) 0.0447430857683
(3, 2, 1) 0.0441280013156
(4, 3, 2) 0.0439614427612
(3, 4, 1) 0.0425776553257
(3, 1, 2) 0.0395797516406
(3, 1, 4) 0.0386301040548
(2, 3, 1) 0.0348951498537

process_multi_race_standouts()[source]

Define single race standouts for first, second, third, fourth, fifth, sixth

Returns:	None

process_single_race_standouts()[source]

Define single race standouts for first, second, third, fourth, fifth, sixth

Returns:	None

rounding = 'Round Up'

type of rounding, one of [“Exact”,”Round Up”,”Round_Down”,”Nearest”]

roundit(y)[source]

Parameters:	y – stake amount
Returns:	stake amount rounded according to rounding parameter

scale_tab = 0

scale TAB market by % (0 is normalized, -1 unscaled, otherwise < 100)

scale_user = 0

scale user market by % (0 is normalized, -1 unscaled, otherwise < 100)

second = []

second place standouts (after [] substitution)

single_race_preprocess()[source]

This routine handles the preprocessing for single race betting pools:

• nraces needs to be 1
• at least one of user odds or TAB odds must be provided
• ensure that odds are only for one race
• list of horse TAB ids must be provided and be of same length as odds provided
• check to make sure jockey and trainer info not provided

Process input in the following order

• remove scratchings, taking care to delete runner info from end of the appropriate lists
• scale TAB and/or user odds
• process standouts

Returns:	Flag for tab divs, flag for user divs, tab prob list, user prob list

single_race_scale_odds(ntabodds, nuserodds)[source]

This routine scales the odds and calculates the relevant probability of the user and/or tab win price line.

Parameters:	ntabodds – 1 if have tab odds, 0 otherwise nuserodds – 1 if have user odds, 0 otherwise
Returns:	tab prob list, user prob list

single_race_scratchings(ntabodds, nuserodds)[source]

Parameters:	ntabodds – 1 if tab odds present, 0 otherwise nuserodds – 1 if user odds present, 0 otherwise
Returns:	None

single_race_validation()[source]

This routine checks for a number of possible input errors for a single race pool.

Returns:

sixth = []

sixth place standouts (after [] substitution)

stake = 0.5

Amount to stake on each combination if flat_stakes is True

standouts_1 = []

list of standouts for first place. Generally speaking, if standouts are given for any place in one race pools or any leg for multi race pools, the rest must be specified as well. If one wants to bet the field then the entry shoud be the empty list.

example for a single race, [1,3,4]

Alternatively for multi-race bets, it standouts for first in the first race

standouts_2 = []

list of standouts for second place. Alternatively for multi-race bets, it standouts for first in the second race

standouts_3 = []

list of standouts for third place. Alternatively for multi-race bets, it standouts for first in the third race

standouts_4 = []

list of standouts for fourth place. Alternatively for multi-race bets, it standouts for first in the fourth race

standouts_5 = []

list of standouts for fifth place. Alternatively for multi-race bets, it standouts for first in the fifth race

standouts_6 = []

list of standouts for sixth place. Alternatively for multi-race bets, it standouts for first in the sixth race

tab_div_range = False

Dividend range for TAB price line; eg, (100,1000), or False for no check

tab_odds = []

list of lists of TAB odds (one list for each race)

tabodds1 = []

1st favourite restricted to (min,max) tab odds, empty list accept all odds

tabodds2 = []

2nd favourite restricted to (min,max) tab odds, empty list accept all odds

tabodds3 = []

3rd favourite restricted to (min,max) tab odds, empty list accept all odds

tabodds4 = []

4th favourite restricted to (min,max) tab odds, empty list accept all odds

tabodds5 = []

5th favourite restricted to (min,max) tab odds, empty list accept all odds

tabodds6 = []

6rd favourite restricted to (min,max) tab odds, empty list accept all odds

takeout = 100

Takeout amount

takeout_priceline = 'tab'

price line use for takeout cqalculation, must be one of [“tab”,”user”]

third = []

third place standouts (after [] substitution)

trainer_list = []

list of lists of trainer lists (one for each race) This parameter is only for multiple race bets.

user_div_range = False

Dividend range for user price line; eg, (100,1000), or False for no check

user_odds = []

list of lists of user odds (one list for each race)

userodds1 = []

1st favourite restricted to (min,max) user odds, empty list accept all odds

userodds2 = []

2nd favourite restricted to (min,max) user odds, empty list accept all odds

userodds3 = []

3rd favourite restricted to (min,max) user odds, empty list accept all odds

userodds4 = []

4th favourite restricted to (min,max) user odds, empty list accept all odds

userodds5 = []

5th favourite restricted to (min,max) user odds, empty list accept all odds

userodds6 = []

6rd favourite restricted to (min,max) user odds, empty list accept all odds