实验一 感知器及其应用
【作业信息】
| 作业课程 | 机器学习 |
|---|---|
| 作业要求 | 作业要求 |
| 作业目标 | 感知器及其应用 |
| 学号 | 3180205402 |
一、实验目的
-
理解感知器算法原理,能实现感知器算法;
-
掌握机器学习算法的度量指标;
-
掌握最小二乘法进行参数估计基本原理;
-
针对特定应用场景及数据,能构建感知器模型并进行预测。
二、实验内容
-
安装Pycharm,注册学生版。
-
安装常见的机器学习库,如Scipy、Numpy、Pandas、Matplotlib,sklearn等。
-
编程实现感知器算法。
-
熟悉iris数据集,并能使用感知器算法对该数据集构建模型并应用。
三、实验报告要求
-
按实验内容撰写实验过程;
-
报告中涉及到的代码,每一行需要有详细的注释;
-
按自己的理解重新组织,禁止粘贴复制实验内容!
四、实验过程及步骤
实验代码
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris #载入Fisher的鸢尾花数据
import matplotlib.pyplot as plt
#Matplotlib是Python的一个绘图库,是Python中最常用的可视化工具之一,可以非常方便地创建2D图表和一些基本的3D图表pyplot模块的plot函数可以接收输入参数和输出参数,还有线条粗细等参数
%matplotlib inline
# load data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names) #是一个表格
df['label'] = iris.target # 表头字段就是key
df.plot(figsize = (12, 8)) # 利用dataframe做简单的可视化分析
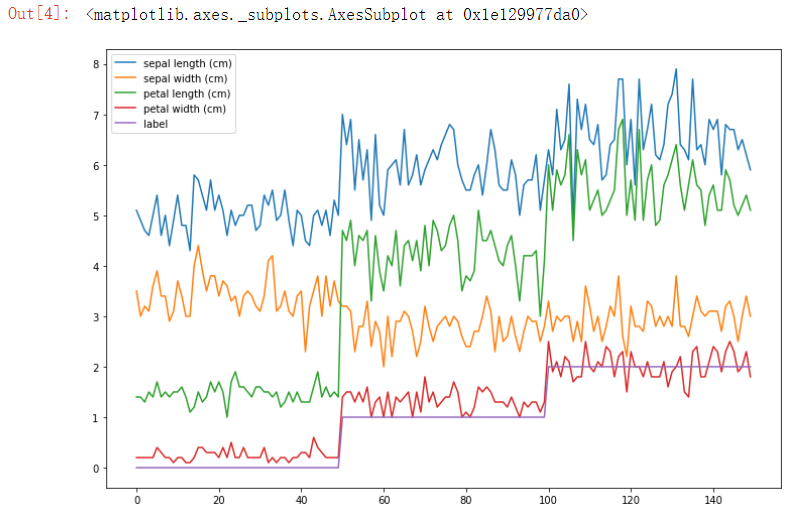
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label'] # 选择其中的4个特征进行训练
df.label.value_counts()

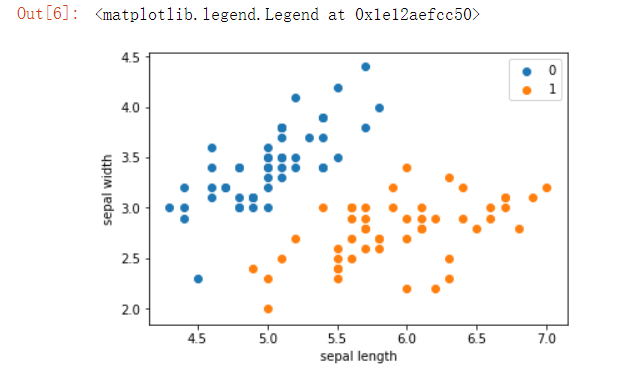
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
data = np.array(df.iloc[:100, [0, 1, -1]]) # 取前100条数据,为了方便展示,取2个特征
X, y = data[:,:-1], data[:,-1] # 数据类型转换,为了后面的数学计算
y = np.array([1 if i == 1 else -1 for i in y])
# 数据线性可分,二分类数据
# 此处为一元一次线性方程
class Model:
def __init__(self):
self.w = np.ones(len(data[0])-1, dtype=np.float32)
self.b = 0 #初始w/b的值
self.l_rate = 0.1
# self.data = data
def sign(self, x, w, b):
y = np.dot(x, w) + b #求w,b的值
#Numpy中dot()函数主要功能有两个:向量点积和矩阵乘法。
#格式:x.dot(y) 等价于 np.dot(x,y) ———x是m*n 矩阵 ,y是n*m矩阵,则x.dot(y) 得到m*m矩阵
return y
# 随机梯度下降法
#随机梯度下降法(SGD),随机抽取一个误分类点使其梯度下降。根据损失函数的梯度,对w,b进行更新
def fit(self, X_train, y_train): #将参数拟合 X_train数据集矩阵 y_train特征向量
is_wrong = False
#误分类点的意思就是开始的时候,超平面并没有正确划分,做了错误分类的数据。
while not is_wrong:
wrong_count = 0 #误分为0,就不用循环,得到w,b
for d in range(len(X_train)):
X = X_train[d]
y = y_train[d]
if y * self.sign(X, self.w, self.b) <= 0:
# 如果某个样本出现分类错误,即位于分离超平面的错误侧,则调整参数,使分离超平面开始移动,直至误分类点被正确分类。
self.w = self.w + self.l_rate*np.dot(y, X) #调整w和b
self.b = self.b + self.l_rate*y
wrong_count += 1
if wrong_count == 0:
is_wrong = True
return 'Perceptron Model!'
#线性可分可用随机梯度下降法
def score(self):
pass
# 拟合
perceptron = Model()
perceptron.fit(X, y)
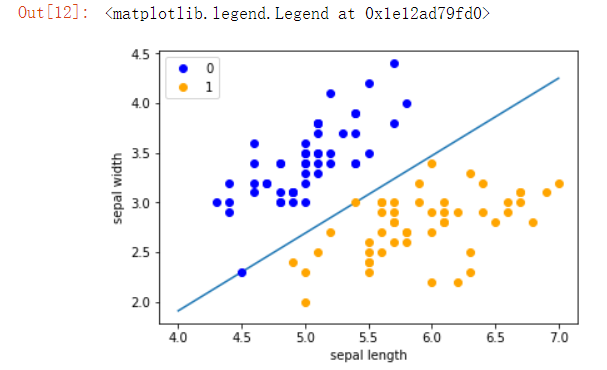
x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
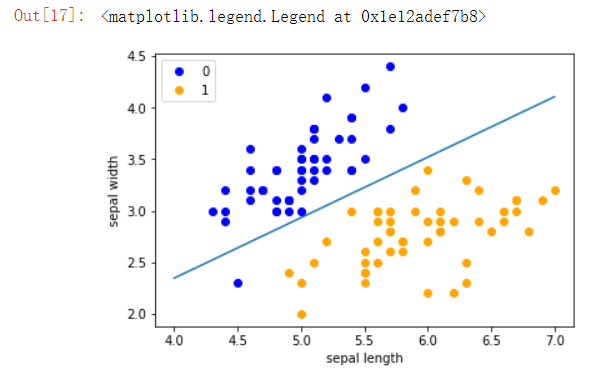
plt.plot(x_points, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
#定义感知机
from sklearn.linear_model import Perceptron
#使用训练数据进行训练
clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False)
#得到训练结果,权重矩阵
clf.fit(X,y)

# Weights assigned to the features.输出特征权重矩阵
print(clf.coef_)
[[ 74.6 -127.2]]
# 超平面的截距 Constants in decision function.
print(clf.intercept_)
[0.]
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
五、实验小结
最小二乘估计法是对过度确定系统,即其中存在比未知数更多的方程组,以回归分析求得近似解的标准方法。在这整个解决方案中,最小二乘法演算为每一方程式的结果中,将残差平方和的总和最小化。
最重要的应用是在曲线拟合上。最小平方所涵义的最佳拟合,即残差(残差为:观测值与模型提供的拟合值之间的差距)平方总和的最小化。
当问题在自变量有重大不确定性时,那么使用简易回归和最小二乘法会发生问题;在这种情况下,须另外考虑变量-误差-拟合模型所需的方法,而不是最小二乘法。
最小二乘法所得出的多项式,即以拟合曲线的函数来描述自变量与预计应变量的变异数关系。



