二维离散余弦变换编码

2020-05-2213:57:51

变换编码就是换一种表示方式来表示原始数据,或者说在不同于原始空间的变换空间中来描述原始数据,以使数据获得某些特点,这些特点有助于获得更好的编码效果。

变换编码原理：

尽管图像变换本身并不带来数据压缩，但由于变换后系数之间的相关性明显降低，图像的大部分能量只集中到少数几个变换系数上，采用适当的量化和熵编码可以有效地压缩图像的数据量。图像经某些变换后，系数的空间分布和频率特性有可能与人眼的视觉特性匹配，因此可以利用人类视觉系统的生理和心理特点来得到较好的编码系统。

变换编码通常是将空间域相关的像素点通过正交变换映射到频域上，使变换后的系数之间的相关性降低。数据变换后在频域上应满足：所有的系数相互独立；能量集中在少数几个系数上；这些系数集中在一个最小的区域内。

变换的意义：

是有失真编码中应用最广泛的一类编码方法，与预测编码一样，均为通过去除信源序列的相关性来达到数据压缩的目的。与预测编码的不同之：预测编码是在空间域或时间域内进行的，而变换编码则是在变换域（频率域）内进行的。

映射变换的方法很多，一般是指函数变换法，而常用的是正交变换法。可以使函数的某些特性变得明显，使问题的处理得到简化。在图像数据压缩技术中，正交变换编码（以下简称变换编码）与预测编码一起成为最基本的两种编码方法。人们最熟悉的是傅里叶变换(FT)、K - L 变换、离散余弦变换(DCT) 、小波变换(WT)。

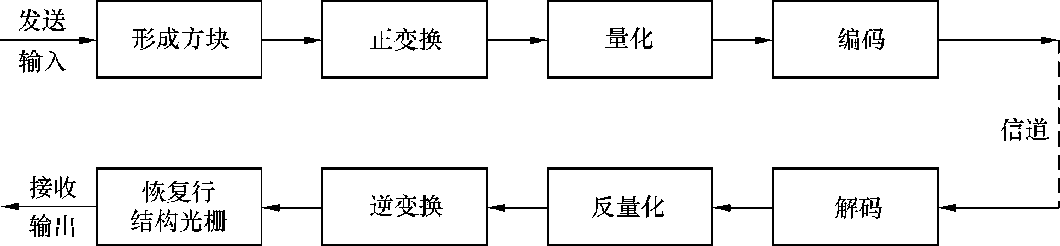
二维离散余弦编码：

核函数为：

由于DCT 变换构成的基向量与图像具体内容无关,且变换是可分离的,故可通过两个一维DCT 变换得到二维DCT 变换。即先对图像的每一行进行一维DCT 变换,再对每一列进行一维DCT 变换。二维离散IDCT 也可以通过两次一维IDCT 得到。 DCT 有快速算法,使得运算的复杂度大大降低,从而减少了编解码延迟。

应用举例：

编码某个图象的一个8*8方块的亮度值。

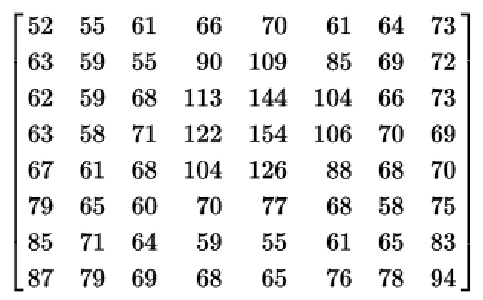
int a[8][8] = { {52,55,61,66,70,61,64,73},
                    {63,59,55,90,109,85,69,72},
                    {62,59,68,113,144,104,66,73},
                    {63,58,71,122,154,106,70,69},
                    {67,61,68,104,126,88,68,70},
                    {79,65,60,70,77,68,58,75},
                    {85,71,64,59,55,61,65,83},
                    {87,79,69,68,65,76,78,94} };

由于一个字节是0~255，为了减小绝对值波动，先把数值移位一下，变成-128~127。

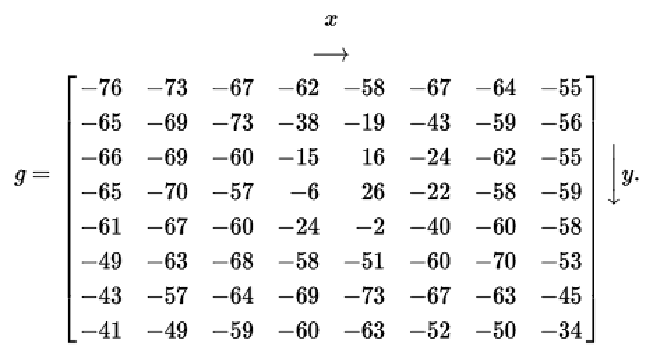
//循环定义b矩阵
for (x = 0; x < r; x++){
        for (y = 0; y < c; y++)
        {
            b[x][y] = 128;
        }
    }
//数组移位
for (x = 0; x < r; x++){
        for (y = 0; y < c; y++) {
            g[x][y] = a[x][y] - b[x][y];
        }
    }

接着，根据DCT变换公式，各种计算，获得临时结果。（下公式中去掉1/4计算）

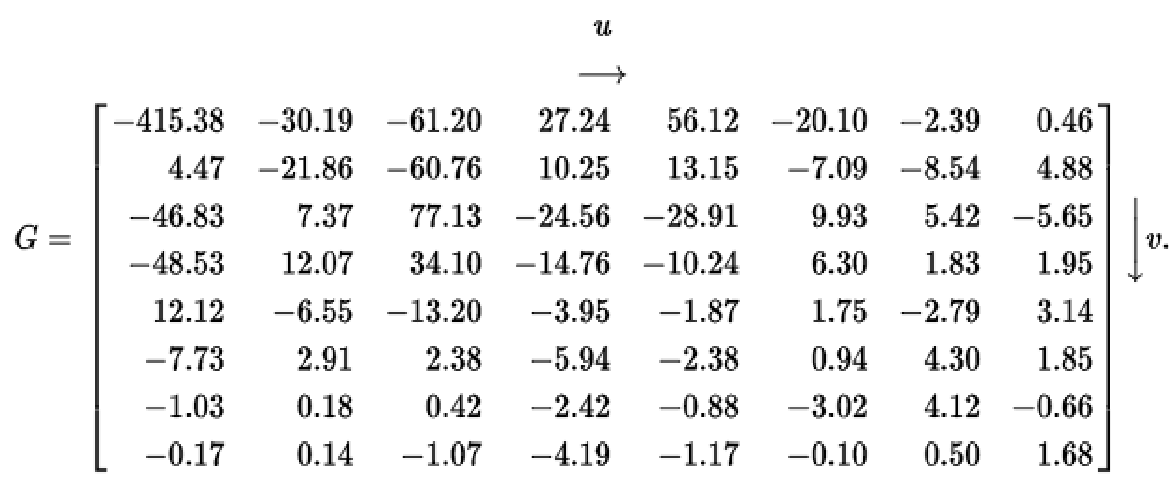
for (u = 0; u < r; u++){
        for (v = 0; v < c; v++) {
            double cos_product = 0.;
            if (u == 0) {
                a_u = 1. / sqrt((double)r);
            }
            else {
                a_u = sqrt(2. / (double)r);
            }
            if (v == 0) {
                a_v = 1. / sqrt((double)r);
            }
            else {
                a_v = sqrt(2. / (double)r);
            }
            
            /*printf("a_u:\n");
            printf("%3.2f  ", a_u);
            if (v == c - 1)
                printf("\n");*/
            for (x = 0; x < r; x++)
                for (y = 0; y < c; y++) {
                    cos_product += (double)g[x][y] * cos(((2. * (double)x + 1.) * (double)u * pai) / (2. * (double)r))
                        * cos(((2. * (double)y + 1.)* (double)v * pai) / (2. * (double)r));
                }
            G[u][v] = a_u * a_v * cos_product;
        }
    }

    
    printf("\nDCT变换后矩阵G:\n\n");
    for (u = 0; u < r; u++){
        for (v = 0; v < c; v++) {
            printf("%9.2f  ", G[u][v]);
            if (v == c - 1)
                printf("\n");
        }
    }

根据亮度量化系数矩阵

获得量化结果：（上一页表G除以上面的表Q，四舍五入）

    int B[8][8], Q[8][8] = { {16,11,10,16,24,40,51,61},
                    {12,12,14,19,26,58,60,55},
                    {14,13,16,24,40,57,69,56},
                    {14,17,22,29,51,87,80,62},
                    {18,22,37,56,68,109,103,77},
                    {24,35,55,64,81,104,113,92},
                    {49,64,78,87,103,121,120,101},
                    {72,92,95,98,112,100,103,99} };
    printf("\n亮度化后矩阵B:\n\n");
    for (x = 0; x < r; x++) {
        for (y = 0; y < c; y++) {
            B[x][y] = round(G[x][y] / Q[x][y]);
            printf("%6d  ", B[x][y]);
            if (y == c - 1)
                printf("\n");
        }
    }

可见，新的数据，很小，很多是0。这么多0，完全可以用游程编码，大大缩小数据量。

解码：

先游程编码恢复，然后，根据量化表，恢复得到

再根据反离散余弦变换的公式：（下公式中去掉1/4计算）

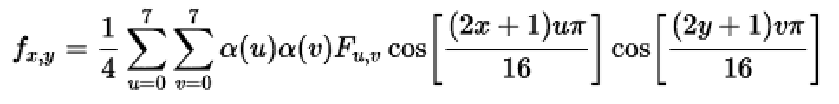
再右移127，恢复原始数据。

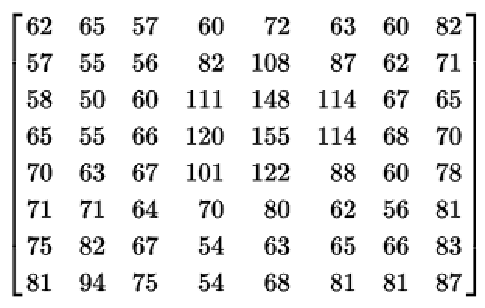
源代码放在github上 https://github.com/C-O-L/DCT-IDCT

posted @ 2020-05-22 13:58 C-O-L 阅读(1216) 评论(0) 编辑收藏举报

刷新页面返回顶部

C-O-L

二维离散余弦变换编码

公告