LeetCode刷题之——62. Unique Paths(单一路径)

62. Unique Paths(机器人走网格的单一路径数量)

 

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

 

 

 

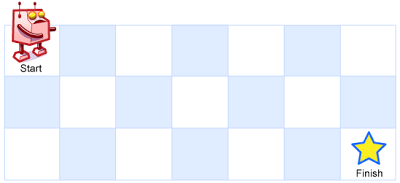
Constraints:

• 1 <= m, n <= 100
• It's guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.

 

---

以上是问题描述。

我的算法如下：

假设一个3*7的网格：

 

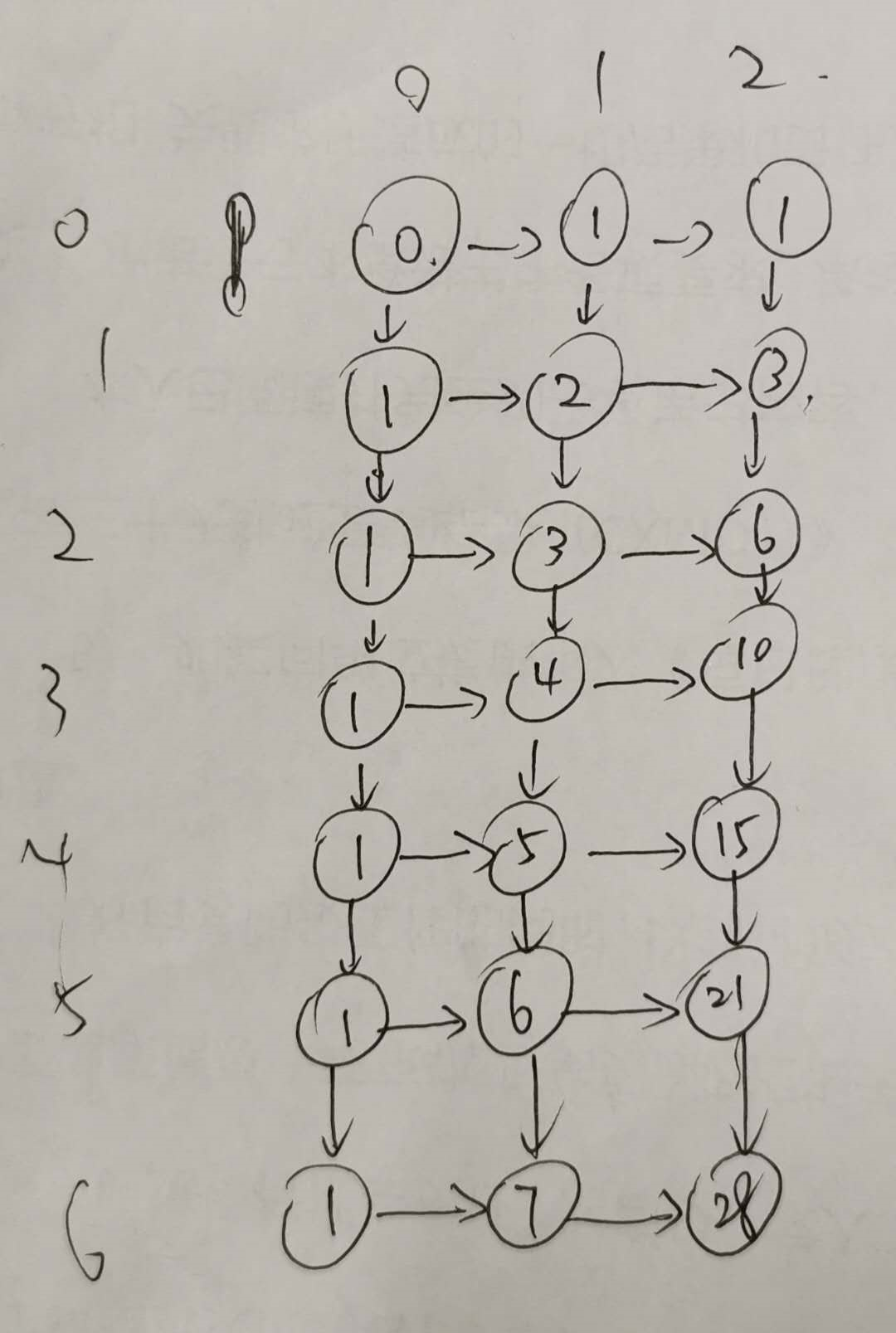
大概的思想是这样的：看一下对于除去左上角0,0的剩余所有点中的任意一点来说，从左上角0,0走到这一点有几条路。（简称路径数）

比如，最左侧和最上面的所有点都只有一条路径（直线），因为机器人只能往下或者往右走。

由此，可以算出剩下任意一点的路径数：路径数 = 左侧点的路劲数 + 上侧点的路径数。

那么到右下角的点的路径数也就非常容易知道了。

代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) {
        int** mat =new int *[m];
        for(int i=0;i<m;i++){
            mat[i] = new int[n];
        }
            
        
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                    mat[i][j]=1;
            }
        }
        
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                mat[i][j]=mat[i-1][j]+mat[i][j-1];
            }
        }
        
        int res= mat[m-1][n-1];
            
        for(int i=0;i<m;i++)
        delete []mat[i];
    delete []mat;
        
        return res;
        
    }
};

注：难度为medium