使用DFS来拆分强连通分量的算法实现
主要方法:
参考:https://www.cnblogs.com/LLGemini/p/4725952.html

一些数据类型的定义:
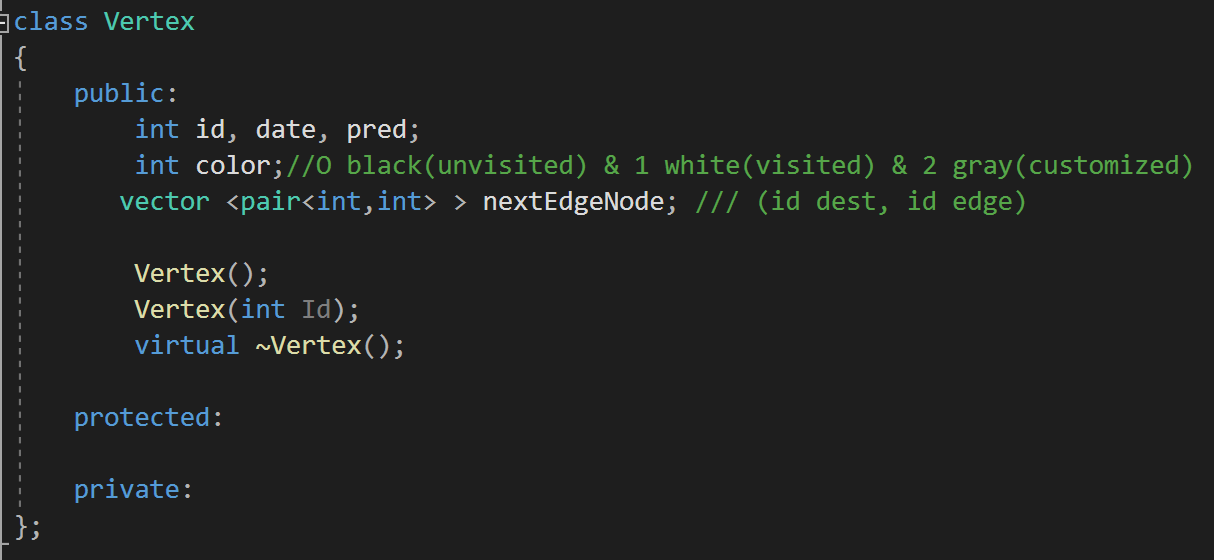
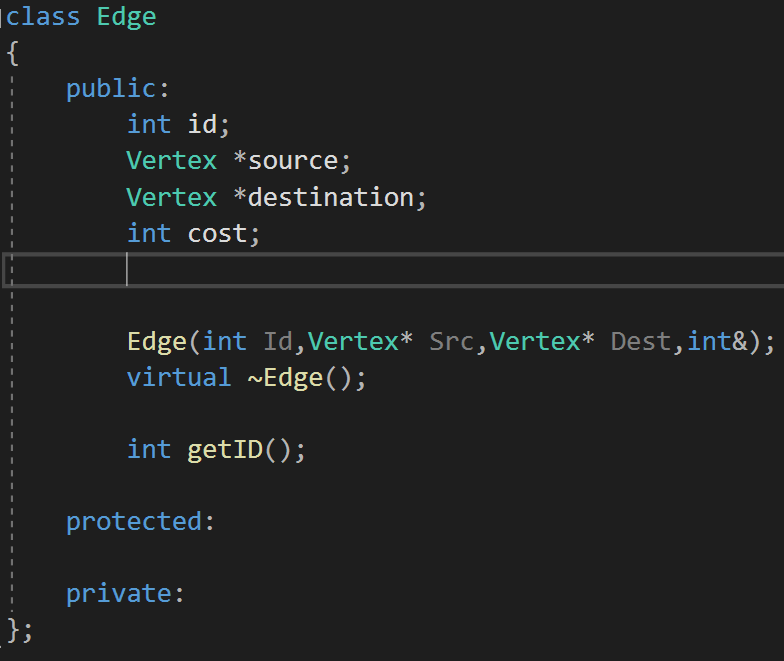

Seperate strongly connected components in a directed graph with DFS:
1 int MaxIndex(int* v, int size) { 2 int max = v[0]; 3 int i = 0; 4 for (auto it = 1; it < size; it++) { 5 if (v[it] > max) { 6 max = v[it]; 7 i = it; 8 } 9 10 } 11 return i; 12 } 13 void Graph::StronglyConnectedComp(int nbNodes,int startFrom) { 14 cout << "Detecting strongly connected components: " << endl; 15 /*choose a vertex randomly or designate with parameter*/ 16 srand((unsigned int)time(NULL)); 17 Vertex* tempV; 18 if (startFrom == -1) { 19 int sze = listVertex.size(); 20 int rdm = rand() % sze;//[0,sze) 21 tempV = listVertex[rdm]; 22 } 23 else 24 tempV = listVertex[startFrom - 1]; 25 int count = 0;// to check if all vertices have been visited 26 int* mark = new int[nbNodes];// to store the numbers marked on vertex 27 stack<Vertex* > myStack;// to assist dfs algo 28 myStack.push(tempV);//initialization 29 /*DFS algo to mark the vertices from leaves*/ 30 while (!myStack.empty()) { 31 cout << "colored:" << myStack.top()->id << endl; 32 myStack.top()->color = 1;// visit the vertex on top 33 int visited = 0;// to check if all adjacent vertices have been visited 34 35 for (auto it = myStack.top()->nextEdgeNode.begin(); it != myStack.top()->nextEdgeNode.end(); it++) { 36 if (listVertex[it->first - 1]->color == 0)//O black(unvisited) & 1 white(visited)) 37 { 38 myStack.push(listVertex[it->first - 1]); 39 break; 40 } 41 else 42 visited++; 43 } 44 /*if the vertex and all its adjacent vertices have been visited, 45 which means the end of DFS, then mark it and pop it out*/ 46 if (visited == myStack.top()->nextEdgeNode.size() && myStack.top()->color == 1) { 47 cout << "mark:" << myStack.top()->id<<endl; 48 count++; 49 mark[myStack.top()->id] = count;// mark the vertex 50 myStack.pop(); 51 } 52 /*check if all vertices in graph have been visited*/ 53 if (myStack.empty() && count < nbNodes) { 54 for (auto it = listVertex.begin(); it != listVertex.end(); it++) { 55 if ((*it)->color == 0) {//O black(unvisited) & 1 white(visited) 56 myStack.push(*it); 57 break; 58 } 59 } 60 } 61 } 62 /*end of DFS and the marking procedure*/ 63 /*restore the visit flag*/ 64 for (auto it = listVertex.begin(); it != listVertex.end(); it++) { 65 (*it)->color = 0;//O black(unvisited) & 1 white(visited) 66 } 67 68 for (auto it = 0; it < nbNodes; it++) 69 cout << "it:" << it << "number:" << mark[it] << endl; 70 /*begin to reverse the edges with no change of original data*/ 71 vector<int>* tempAdjList = new vector<int>[nbNodes];//temporary assisting structure 72 int max = MaxIndex(mark,nbNodes); 73 cout << "maxindex:" << max << endl; 74 for (auto it = listEdges.begin(); it != listEdges.end(); it++) { 75 Vertex* temp; 76 temp = (*it)->destination; 77 (*it)->destination = (*it)->source; 78 (*it)->source = temp; 79 //store the just reversed data 80 tempAdjList[(*it)->source->id].push_back((*it)->destination->id); 81 } 82 myStack.push(listVertex[max]);//initialization 83 mark[max] = 0; 84 int component = 0; 85 int pushchecker = 1; 86 while (!myStack.empty()) { 87 if (myStack.top()->color == 0) { 88 cout << "This is strongly connected component " << component+1 << "." << endl; 89 myStack.top()->color = 1;//O black(unvisited) & 1 white(visited) 90 mark[myStack.top()->id] = 0;//exclude visited vertex 91 cout << "Vertex: " << myStack.top()->id + 1 << endl; 92 } 93 int popchecker = 0; 94 for (auto it = tempAdjList[myStack.top()->id].begin(); it != tempAdjList[myStack.top()->id].end(); it++) { 95 if (listVertex[*it]->color == 0) {//O black(unvisited) & 1 white(visited) 96 myStack.push(listVertex[*it]); 97 pushchecker++; 98 break; 99 } 100 else 101 popchecker++; 102 } 103 if (popchecker == tempAdjList[myStack.top()->id].size() && myStack.top()->color == 1)//O black(unvisited) & 1 white(visited) 104 {// end of the road, pop 105 myStack.pop(); 106 } 107 /*if the current component is all visited and not all vertices in graph are visited, 108 then add the vertex with the biggest number marked into stack*/ 109 if (myStack.empty() && pushchecker < nbNodes) { 110 myStack.push(listVertex[MaxIndex(mark,nbNodes)]); 111 pushchecker++; 112 component++; 113 } 114 } 115 116 delete[] mark; 117 }
测试数据1:
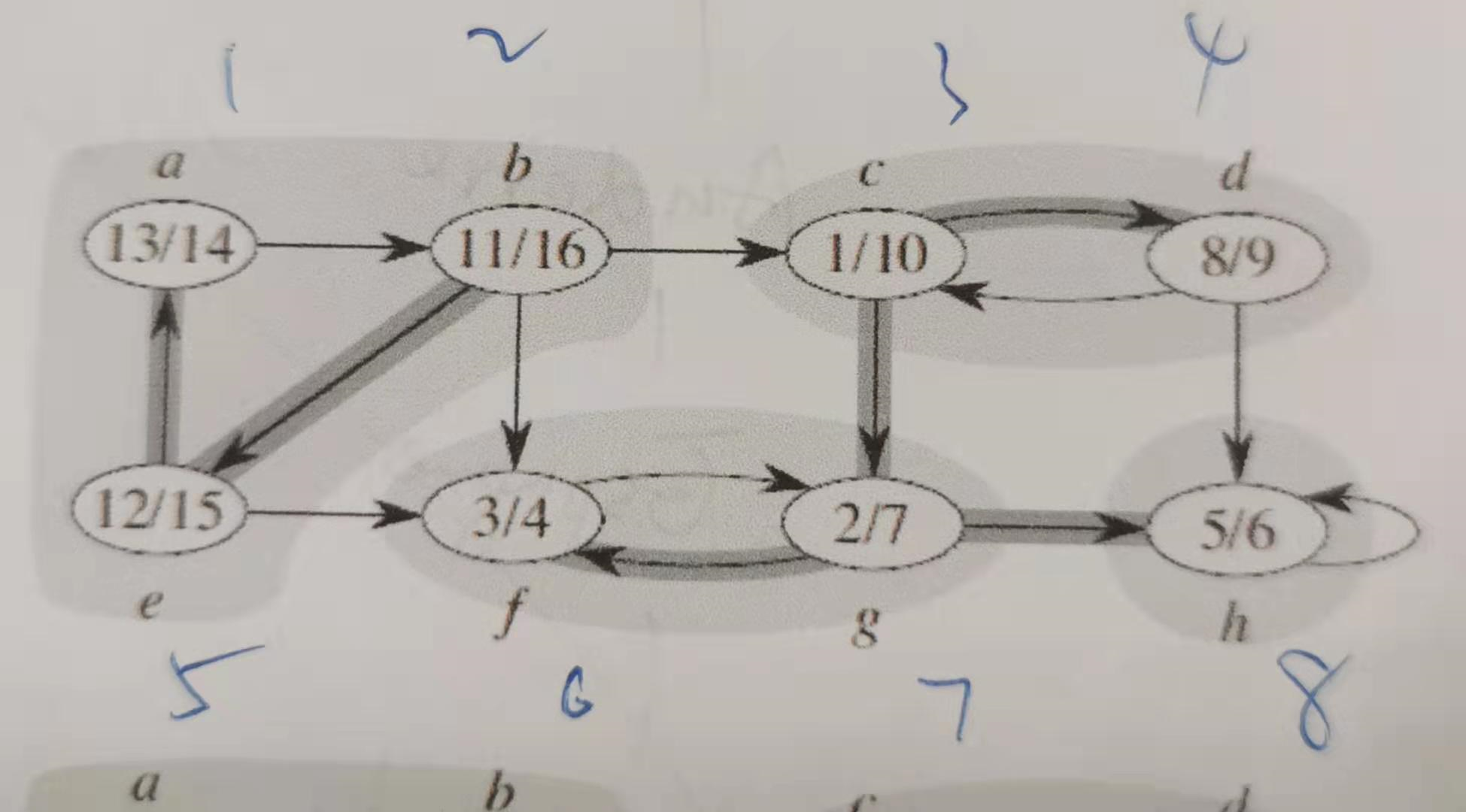
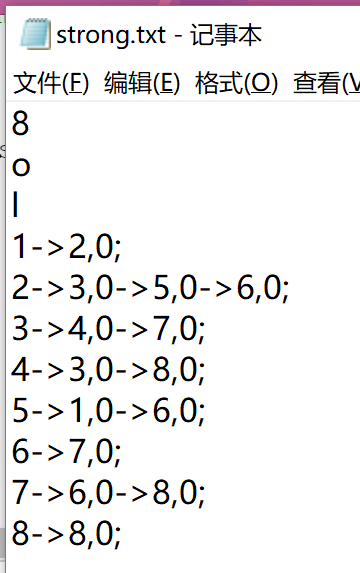
结果:

成功
测试数据2:


结果:

成功



