二叉搜索树(结点添加、后继搜索、前驱搜索、结点删除)
结点的添加:
一开始没有看书没有查,自己写了一个,花了好久才调试成功:
1 bool BST::Add_Node(TreeNode* temp) { 2 if (!root) { 3 root = temp; 4 return true; 5 } 6 TreeNode* current = root; 7 while (current) { 8 if (temp->getData() >= current->getData()) { 9 if (current->getRightChild()) 10 current = current->getRightChild(); 11 else 12 break; 13 } 14 else if (temp->getData() < current->getData()) { 15 if (current->getLeftChild()) 16 current = current->getLeftChild(); 17 else 18 break; 19 } 20 else return false; 21 } 22 temp->setParent(current); 23 if (temp->getData() < current->getData()) 24 current->setLeftChild(temp); 25 else 26 current->setRightChild(temp); 27 return true; 28 }
结点数据:
![]()
构造成功后数据结构应该如图所示:
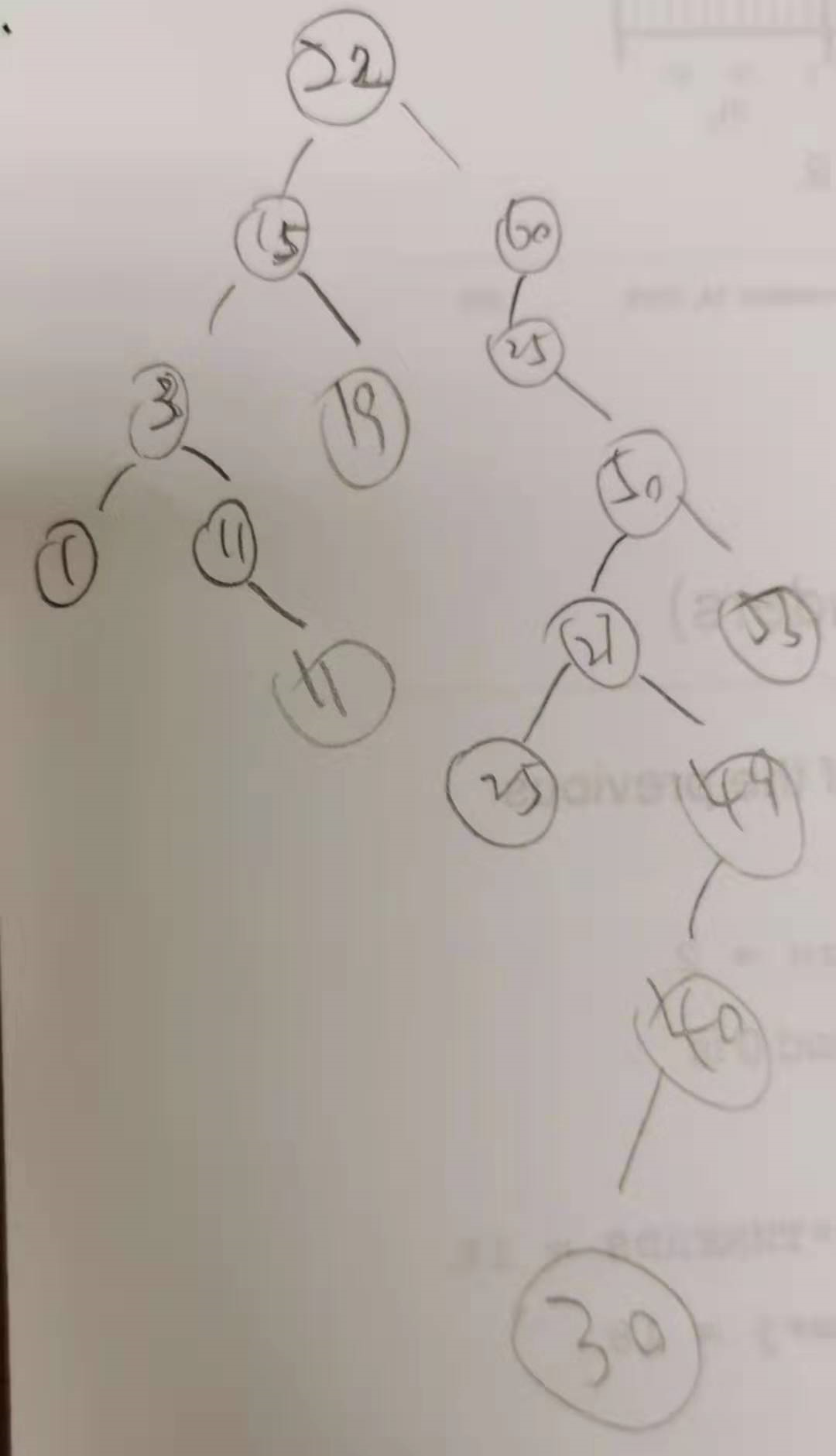
这里对于有重复键值的结点的加入是这样的:(见8-12行)允许重复值的加入,如碰到相同值的结点,则将当前指针指向这个结点的右孩子。
其实这里对二叉搜索树的定义参考的是《算法导论》,其中是允许重复值的:
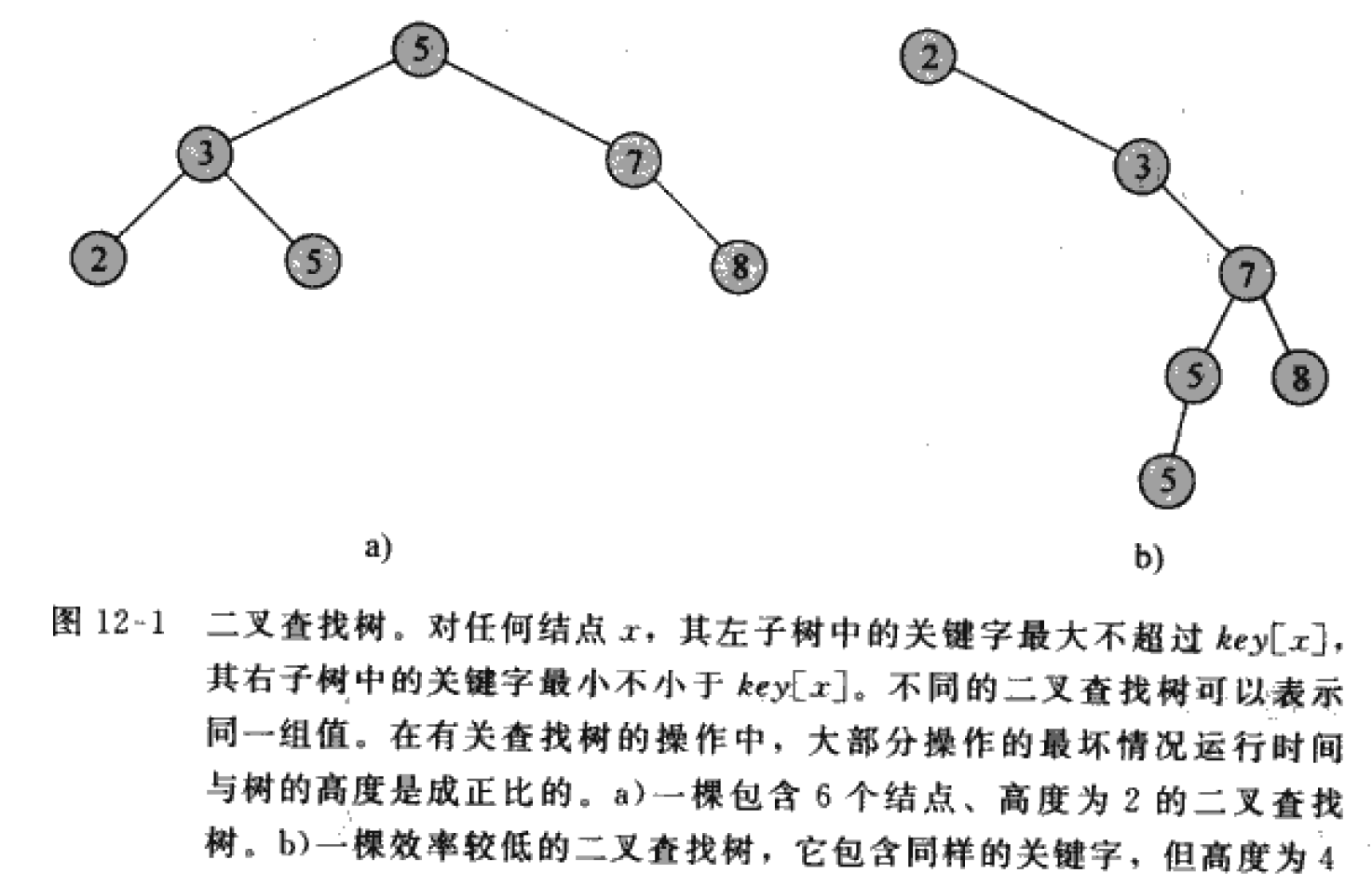
如果想排除重复值,略微修改代码即可,很容易,不再叙述。
以上算法通过先序遍历验证,成功:
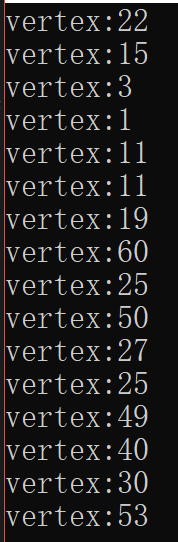
再看《算法导论》中对于结点添加算法的描述:

后继搜索:
看《算法导论》:

假设y是x的后继(即中序排序:······x,y·········),如果x没有右子树,则y是x的最低的祖先,且y的左孩子也是x的祖先。
(这里,一个结点的“祖先”也包括结点本身)
所以换成人话就是:
假设y是x的后继,如果x没有右子树,则y是x的最低的祖先,且y的左孩子是x的祖先或x本身。

因此,想找到y,只需要从x开始向上走,直到找到一个是其父结点的左孩子的结点。

二叉搜索树中,找任一结点的后继是什么思路呢?
如果右孩子非空,那非常好理解,直接找右子树上的最小值就是它的后继。
至于右孩子非空,那么其后继一定在他头顶上;倒过来想,当这个结点被添加进树的时候,由于比后继小,一定加在了其后继的左子树的某个位置上。
这样就很好理解上面粗体字的结论了,如果把结点x后继的左子树独立出来看,x要么是这棵树(我们叫它T'好了)的根结点,要么是非根的某个结点。(x∈T')
这么看来,上面代码就很好理解了:假设p是结点x的后继;先从结点本身这一层开始找起,p不断往上爬,t跟着它爬,每次一层,只要t还是p的右孩子,就说明p还不是后继,就继续往上爬。相当于我们从x开始找其所在的子树T'的根节点。
或者还有一种更简单的理解:从结点x开始向上(包括x,因为x可能是T'的根结点)寻找一对父子结点p-t,父子结点对p-t满足:p键值>t键值;则找到的第一对父子结点p-t中的父节点p即为x的后继结点。
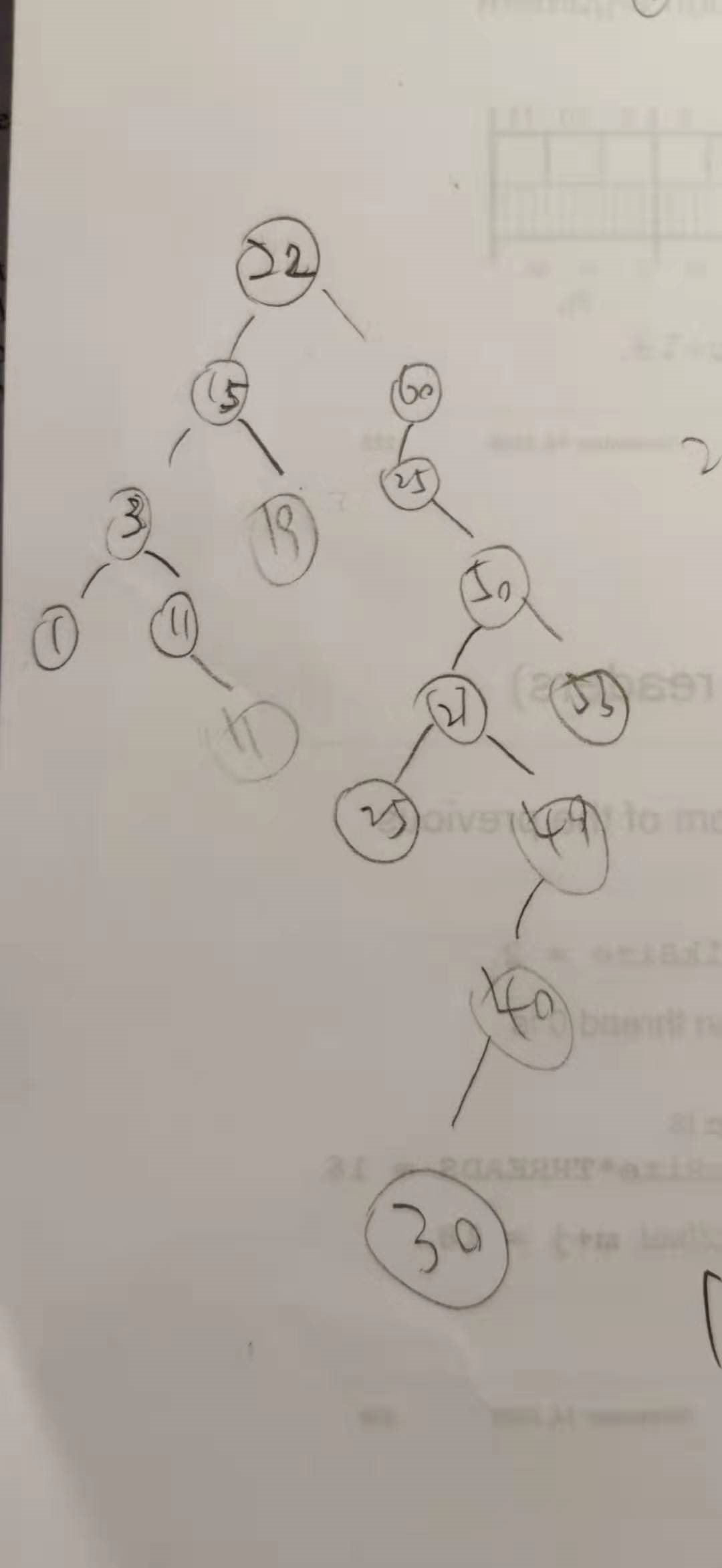
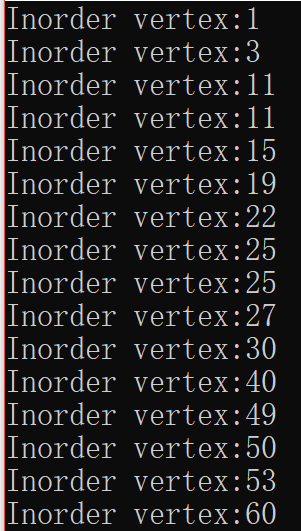
把上面的二叉搜索树用中序遍历跑一下,对比着看,帮助理解。
重复键值嫌麻烦没有改,不影响理解。
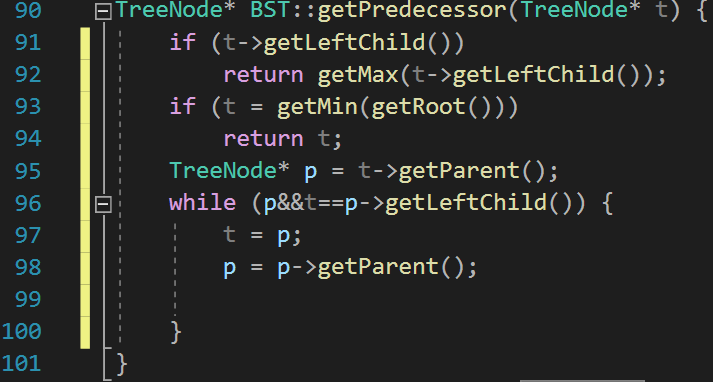
前驱搜索:
本身逻辑其实一模一样,把后继搜索反过来就行了
结点删除:
直接看算法导论:
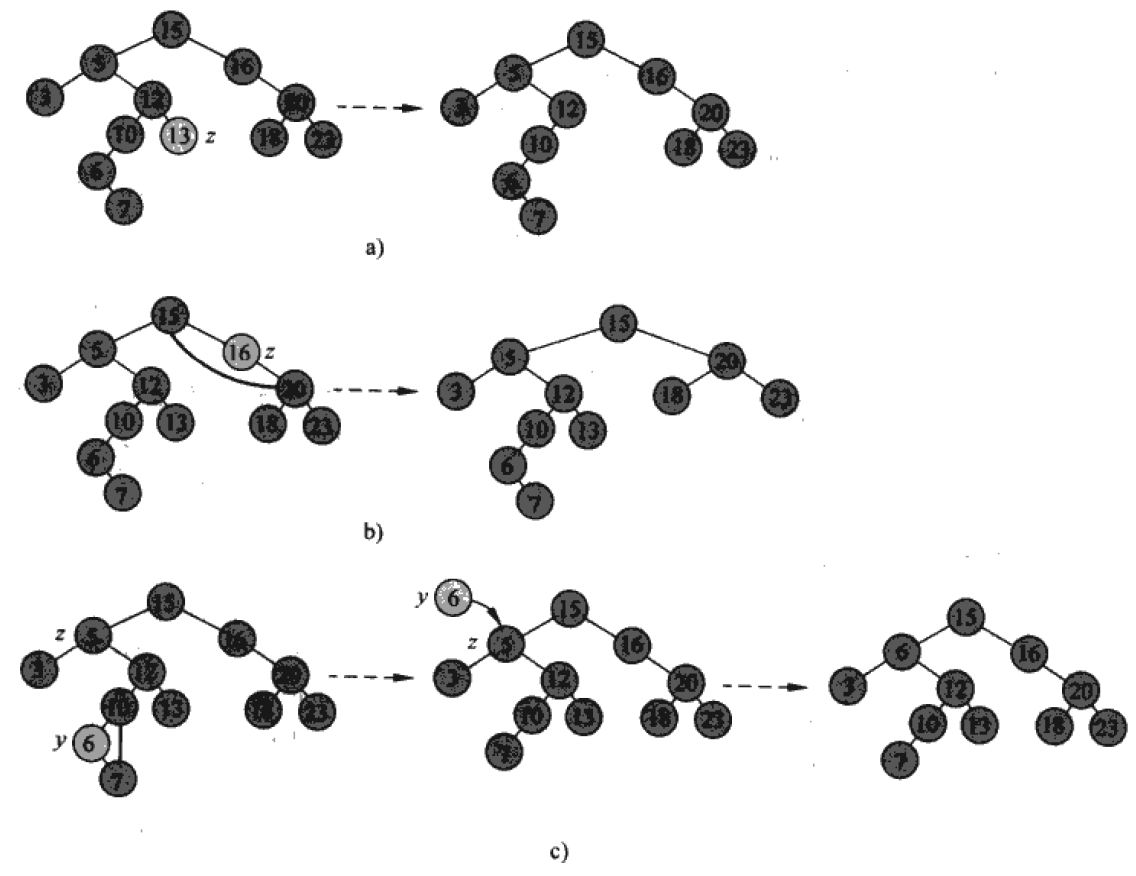
分成了三类:
1、如果要删除的结点没有孩子:直接将他的父结点对应的指针(左或右)指空,并删除他。
2、如果要删除的结点有1个孩子:直接将他的父结点对应的指针(左或右)指向他唯一的那个孩子,并删除他。
3、如果要删除的结点有2个孩子: 把他用他的后继结点代替。
以下是算法代码(由于使用的数据结构和出于简便的考虑,没有真正删除结点数据,只是删除了其关联信息)


测试删除50:
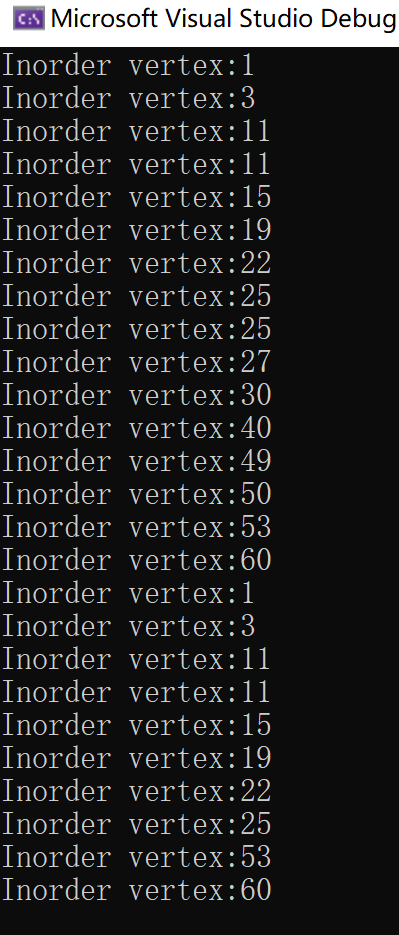
成功。
这里算法有个bug,如果删除根节点会出错,因为其父结点为null,访问null的左右孩子其实是不存在的,会抛出访问异常。


