numpy基础--线性代数
以下代码的前提:import numpy as np
线性代数(如矩阵乘法、矩阵分解、行列式以及其他方阵数学等)是任何数组库的重要组成部分。numpy提供了一个用于矩阵乘法的dot函数(既是一个数组方法也是numpy命名空间中的一个函数)。
矩阵乘法官方说明:numpy.dot — NumPy v1.21 Manual
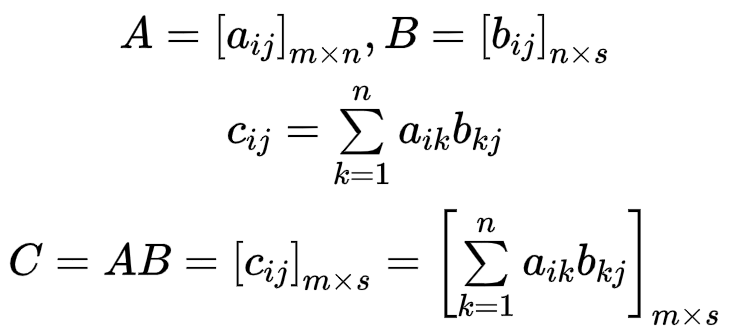
1 >>> x = np.array([[1, 2, 3], [4, 5, 6]])
2 >>> y = np.array([[1, 2], [3, 4], [5, 6]])
3 >>> x
4 array([[1, 2, 3],
5 [4, 5, 6]])
6 >>> y
7 array([[1, 2],
8 [3, 4],
9 [5, 6]])
10 >>> np.dot(x, y)
11 array([[22, 28],
12 [49, 64]])
13 >>> x.dot(y)
14 array([[22, 28],
15 [49, 64]])
16 >>>
numpy.linalg中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西。
1 >>> from numpy.linalg import inv, qr
2 >>> X = np.arange(9).reshape(3, 3)
3 >>> X
4 array([[0, 1, 2],
5 [3, 4, 5],
6 [6, 7, 8]])
7 >>> mat = X.T.dot(X)
8 >>> mat
9 array([[45, 54, 63],
10 [54, 66, 78],
11 [63, 78, 93]])
12 >>> inv(mat)
13 array([[ 3.51843721e+13, -7.03687442e+13, 3.51843721e+13],
14 [-7.03687442e+13, 1.40737488e+14, -7.03687442e+13],
15 [ 3.51843721e+13, -7.03687442e+13, 3.51843721e+13]])
16 >>> mat.dot(inv(mat))
17 array([[ 0.79296875, 1. , -0.2109375 ],
18 [ 0.1484375 , 1. , -0.046875 ],
19 [-0.74609375, 1. , 0.6171875 ]])
20 >>> q, r = qr(mat)
21 >>> q
22 array([[-0.47673129, 0.77849894, 0.40824829],
23 [-0.57207755, 0.07784989, -0.81649658],
24 [-0.66742381, -0.62279916, 0.40824829]])
25 >>> r
26 array([[-9.43927963e+01, -1.15559666e+02, -1.36726535e+02],
27 [ 0.00000000e+00, -1.40129810e+00, -2.80259620e+00],
28 [ 0.00000000e+00, 0.00000000e+00, 3.55271368e-15]])
29 >>>
下表是常用的numpy.linalg函数。
| 方法 | 说明 |
|---|---|
| diag | 以一维数组的形式返回方阵的对角线(或非对角线)元素,或将一维数组转换为方阵(非对角线元素为0) |
| dot | 矩阵乘法 |
| trace | 计算对角线元素的和 |
| det | 计算矩阵行列式 |
| eig | 计算方阵的本征值和本征向量 |
| inv | 计算方阵的逆 |
| solve | 解线性方程组Ax=b,其中A为一个方阵 |
| lstsq | 计算Ax=b的最小二乘解 |
numpy.diag — NumPy v1.21 Manual
numpy.diag(v, k=0):取矩阵主对角线的值,k=0,取主对角线;k>0,取主对角线之上;k<0,取主对角线之下。
>>> x = np.arange(9).reshape(3, 3)
>>> x
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> np.diag(x)
array([0, 4, 8])
>>> np.diag(x, k=1)
array([1, 5])
>>> np.diag(x, k=-1)
array([3, 7])
>>> np.diag(np.diag(x))
array([[0, 0, 0],
[0, 4, 0],
[0, 0, 8]])
numpy.trace — NumPy v1.21 Manual
矩阵的迹:矩阵主对角线元素之和。
>>> x = np.eye(3)
>>> x
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
>>> x.trace()
3.0
numpy.linalg.det — NumPy v1.21 Manual
矩阵(必须是方阵)行列式的值:The determinant of a 2-D array [[a, b], [c, d]] is ad - bc:
>>> a = np.array([[1, 2], [3, 4]])
>>> a
array([[1, 2],
[3, 4]])
>>> np.linalg.det(a)
-2.0000000000000004
numpy.linalg.eig — NumPy v1.21 Manual
方阵的本征值和本征向量:

>>> from numpy import linalg as LA
>>> x = np.diag((1, 2, 3))
>>> x
array([[1, 0, 0],
[0, 2, 0],
[0, 0, 3]])
>>> w, v = LA.eig(x)
>>> w; v
array([1., 2., 3.])
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
numpy.linalg.inv — NumPy v1.21 Manual
矩阵的逆:设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得:AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵。
>>> from numpy.linalg import inv
>>> a = np.array([[1., 2.], [3., 4.]])
>>> a
array([[1., 2.],
[3., 4.]])
>>> ainv = inv(a)
>>> ainv
array([[-2. , 1. ],
[ 1.5, -0.5]])
numpy.linalg.solve — NumPy v1.21 Manual
解线性方程组Ax=b,其中A为一个方阵。
>>> a = np.array([[1, 2], [3, 5]])
>>> b = np.array([1, 2])
>>> x = np.linalg.solve(a, b)
>>> x
array([-1., 1.])


 浙公网安备 33010602011771号
浙公网安备 33010602011771号