numpy基础--ndarray(一种多维数组对象)
NumPy基本介绍
NumPy(Numerical Python)是高性能科学计算和数据分析的基础包。其提供了以下基本功能:
- ndarray:一种具有矢量算术运算和复杂广播能力的快速且节省空间的多维数组。
- 对整体数组进行快速的标准数学运算。
- 线性代数、随级数生成以及傅里叶变换功能。
- 提供简易的C API,可方便的将数据传递给由低级语言编写的外部库,外部库也能以NumPy数组的形势将数据返回给Python。
对于数据分析,需要关心以下几点:
- 数据整理和清理、子集构造和过滤、转换等快速的矢量化数组运算。
- 常用数组算法,如排序、唯一化、集合运算等。
- 高效的描述统计和数据聚合/摘要运算。
官方说明文档:What is NumPy? — NumPy v1.21 Manual
以下代码的前提:import numpy as np
1 NumPy的ndarray:一种多维数组对象
官方API使用说明:The N-dimensional array (ndarray) — NumPy v1.21 Manual
ndarray(N-dimensional array,N维数组对象):是一个快速灵活的大数据集容器。可以利用这种数组对整块数据执行一些数学运算,其语法跟标量元素之间的运算一样。
1 >>> from numpy import array
2 >>> data = array([[0.926, -0.246, -0.8856], [0.5639, 0.2379, 0.9104]])
3 >>> print (data * 10)
4 [[ 9.26 -2.46 -8.856]
5 [ 5.639 2.379 9.104]]
6 >>> data.shape
7 (2, 3)
8 >>> data.dtype
9 dtype('float64')
10 >>>
ndarray是一个通用的同构数据多维数组,也就是所,其中的所有元素必须是相同类型的。每个数组都有一个shape(一个表示各维度大小的元组)和一个dtype(一个用于说明数组数据类型的对象)。
1.1 创建ndarray
创建数组最简单的办法是使用array()函数。它接受一切序列型的对象(包括其他数组),然后产生一个新的含有传入数据的NumPy数组。嵌套序列将会被转换为一个多维数组。
1 >>> from numpy import array
2 >>> data1 = [6, 7.5, 9, 0, 1]
3 >>> arr1 = array(data1)
4 >>> arr1
5 array([6. , 7.5, 9. , 0. , 1. ])
6 >>> data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
7 >>> arr2 = array(data2)
8 >>> arr2
9 array([[1, 2, 3, 4],
10 [5, 6, 7, 8]])
11 >>> arr2.ndim
12 2
13 >>> arr2.shape
14 (2, 4)
15 >>>
np.array之外,还有一些函数也可以创建数组,比如zeros和ones分别创建指定长度或形状的全0或全1数组。empty可以创建一个没有任何具体值的数组,返回的是一些未初始化的垃圾值。
1 >>> import numpy as np
2 >>> np.zeros(10)
3 array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
4 >>> np.zeros((2, 3))
5 array([[0., 0., 0.],
6 [0., 0., 0.]])
7 >>> np.ones(5)
8 array([1., 1., 1., 1., 1.])
9 >>> np.ones((2, 3))
10 array([[1., 1., 1.],
11 [1., 1., 1.]])
12 >>> np.empty((2, 3, 2))
13 array([[[6.23042070e-307, 3.56043053e-307],
14 [1.37961641e-306, 6.23039354e-307],
15 [6.23053954e-307, 9.34609790e-307]],
16
17 [[8.45593934e-307, 9.34600963e-307],
18 [1.86921143e-306, 6.23061763e-307],
注:np.empty任务返回全0数组是不安全的,它返回的都是一些未初始化的垃圾值。
arange()是python内置函数range的数组版本。
1 >>> np.arange(10)
2 array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
下表是数组创建函数:
| 函数 | 说明 |
|---|---|
| array | 将输入数据(列表、元组、数组或其他序列类型)转换为ndarray |
| arange | 类似于内置的range,但返回的是一个ndarray而不是列表 |
| ones、ones_like | 根据指定的形状和dtype创建一个全1数组。ones_like以另一个数组为参数,并根据其形状和dtype创建一个全1数组 |
| zeros、zeros_like | 类似于ones和ones_like,只不过产生的是全0数组 |
| empty、empty_like | 创建新数组,只分配内存空间但不填充任何值,返回的数值都是一些垃圾值 |
| eye、identity | 创建一个正方的NxN单位矩阵(对角线为1,其余为0) |
1.2 ndarray的数据类型
dtype(数据类型)是一个特殊的对象,它含有ndarray将一块内存解释为特定数据类型所需要的信息。
1 >>> arr1 = np.array([1, 2, 3], dtype=np.float64)
2 >>> arr2 = np.array([1, 2, 3], dtype=np.int32)
3 >>> arr1.dtype
4 dtype('float64')
5 >>> arr2.dtype
6 dtype('int32')
NumPy的数据类型:
| 类型 | 类型代码 | 说明 |
|---|---|---|
| int8、uint8 | i1、u1 | 有符号和无符号的8位(1个字节)整型 |
| int16、uint16 | i2、u2 | 有符号和无符号的16位(2个字节)整型 |
| int32、uint32 | i4、u4 | 有符号和无符号的32位(4个字节)整型 |
| int64、uint64 | i8、u8 | 有符号和无符号的64位(8个字节)整型 |
| float16 | f2 | 半精度浮点数 |
| float32 | f4或f | 标准的单精度浮点数,与C的float兼容 |
| float64 | f8或d | 标准的双精度浮点数,与C的double和python的float对象兼容 |
| float128 | f16或g | 扩展精度浮点数 |
| complex64、complex128、complex256 | c8、c16、c32 | 分别用两个32位、64位或128位浮点数表示的复数 |
| bool | ? | 存储True和Fasle值的布尔类型 |
| object | O | python对象类型 |
| string_ | S | 固定长度的字符串类型(每个字符1个字节)。例如要创建一个长度位10的字符串,应使用S10 |
| unicode_ | U | 固定长度的Unicode类型(字节数由平台决定)跟字符串的定义方式一样 |
可通过ndarray的astype方法显式转换其dtype。
1 >>> arr = np.array([1, 2, 3, 4, 5])
2 >>> arr.dtype
3 dtype('int32')
4 >>> float_arr = arr.astype(np.float64)
5 >>> float_arr.dtype
6 dtype('float64')
如果将浮点型转换为整型,则小数部分将会被截断。
1 >>> arr = np.array([1.2, 2.3, 3.4])
2 >>> arr.astype(np.int32)
3 array([1, 2, 3])
如果某字符串表示的全是数字,可以用astype将其转换为数值形式。
1 >>> num_strings = np.array(['1.2', '2.2'], dtype=np.string_)
2 >>> num_strings.astype(float)
3 array([1.2, 2.2])
1.3 数组和标量之间的运算
数组不需要编写循环即可对数据执行批量处理,这通常叫做矢量化(vectorization)。大小相等的数组之间的任何算术运算都会将运算应用到元素级。
1 >>> arr = np.array([[1., 2., 3.], [4., 5., 6.]])
2 >>> arr
3 array([[1., 2., 3.],
4 [4., 5., 6.]])
5 >>> arr * arr
6 array([[ 1., 4., 9.],
7 [16., 25., 36.]])
8 >>> arr - arr
9 array([[0., 0., 0.],
10 [0., 0., 0.]])
11 >>> 1 / arr
12 array([[1. , 0.5 , 0.33333333],
13 [0.25 , 0.2 , 0.16666667]])
14 >>>
不同大小的数组之间的运算叫做广播。
1.4 基本的索引和切片
(1)一维数组和python列表功能类似:
1 >>> arr = np.arange(10)
2 >>> arr
3 array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
4 >>> arr[5]
5 5
6 >>> arr[5:8]
7 array([5, 6, 7])
8 >>> arr[5:8] = 12 # 自动“广播”到整个选区
9 >>> arr
10 array([ 0, 1, 2, 3, 4, 12, 12, 12, 8, 9])
11 >>>
跟列表的最重要的区别在于:数组切片是原始数组的视图,这意味着数据不会被复制,视图上的任何修改都会字节反映到源数组上。
1 >>> arr
2 array([ 0, 1, 2, 3, 4, 12, 12, 12, 8, 9])
3 >>> arr_slice = arr[5:8]
4 >>> arr_slice[1] = 12345
5 >>> arr
6 array([ 0, 1, 2, 3, 4, 12, 12345, 12, 8,
7 9])
8 >>> arr_slice[:] = 64
9 >>> arr
10 array([ 0, 1, 2, 3, 4, 64, 64, 64, 8, 9])
(2)高维度数组
在一个二维数组中,各索引位置上的元素不再是标量而是一维数组。
1 >>> arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
2 >>> arr2d[2]
3 array([7, 8, 9])
4 >>> arr2d[0][2]
5 3
6 >>> arr2d[0, 2] #0行第二个元素
7 3
在高维数组中,如果省略了后面的索引,则返回对象会是一个维度低一点的ndarray(它含有高一级维度上的所有数据)。
1 >>> arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
2 >>> arr3d
3 array([[[ 1, 2, 3],
4 [ 4, 5, 6]],
5
6 [[ 7, 8, 9],
7 [10, 11, 12]]])
8 >>> arr3d[0]
9 array([[1, 2, 3],
10 [4, 5, 6]])
11 >>> old_values = arr3d[0].copy()
12 >>> arr3d[0] = [42]
13 >>> arr3d
14 array([[[42, 42, 42],
15 [42, 42, 42]],
16
17 [[ 7, 8, 9],
18 [10, 11, 12]]])
19 >>> arr3d[0] = old_values
20 >>> arr3d
21 array([[[ 1, 2, 3],
22 [ 4, 5, 6]],
23
24 [[ 7, 8, 9],
25 [10, 11, 12]]])
26 >>> arr3d[1, 0]
27 array([7, 8, 9])
28 >>> arr3d[1, 0, 1]
29 8
1.5 切片索引
ndarray的切片语法和python列表的一维对象类似。
高维度可以在一个或多个轴上进行切片,也可以跟整数索引混合使用。高维数组中切片是沿着一个轴向选取元素的。
1 >>> arr
2 array([ 0, 1, 2, 3, 4, 64, 64, 64, 8, 9])
3 >>> arr[1:6]
4 array([ 1, 2, 3, 4, 64])
5 >>> arr2d
6 array([[1, 2, 3],
7 [4, 5, 6],
8 [7, 8, 9]])
9 >>> arr2d[:2]
10 array([[1, 2, 3],
11 [4, 5, 6]])
12 >>> arr2d[:2, 1:]
13 array([[2, 3],
14 [5, 6]])
15 >>> arr2d[1, :2]
16 array([4, 5])
17 >>> arr2d[2, :1]
18 array([7])
19 >>> arr2d[:, :1]
20 array([[1],
21 [4],
22 [7]])
二维数组切片示例如下:
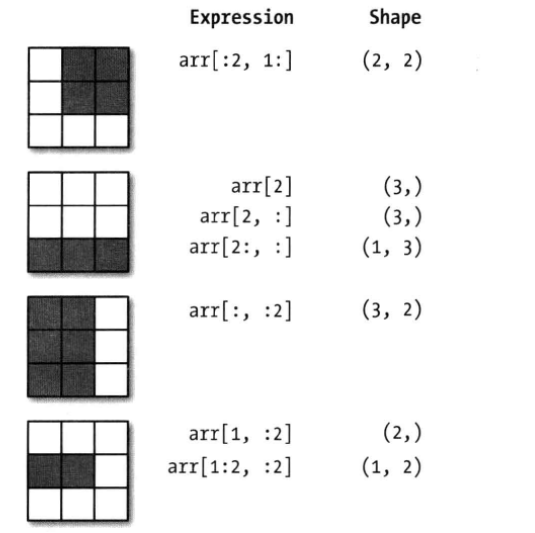
>>> x = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> x
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> x[:2, 1:]
array([[2, 3],
[5, 6]])
>>> x[:2, 1:].shape
(2, 2)
>>> x[2]
array([7, 8, 9])
>>> x[2, :]
array([7, 8, 9])
>>> x[2:, :]
array([[7, 8, 9]])
>>> x[:, :2]
array([[1, 2],
[4, 5],
[7, 8]])
>>> x[1, :2]
array([4, 5])
>>> x[1:2, :2]
array([[4, 5]])
>>>
1.6 布尔型索引
使用一个例子进行说明:假设有一个用于存储数据的数组和一个存储姓名的数组。
1 >>> names = np.array(['bob', 'joe', 'will', 'bob', 'will', 'joe', 'joe'])
2 >>> data = np.random.randn(7, 4) #正态分布的随机数据
3 >>> names
4 array(['bob', 'joe', 'will', 'bob', 'will', 'joe', 'joe'], dtype='<U4')
5 >>> data
6 array([[-0.3246959 , 0.03063124, -0.07431197, -0.9655177 ],
7 [ 0.04598137, -0.62187278, 0.46909509, -0.26366901],
8 [-1.52794074, 1.08687233, -1.84679164, 0.65460423],
9 [ 0.51445349, -0.27982821, 0.81788033, 0.82924586],
10 [ 0.32757133, -0.82471501, -2.76623431, -0.52545958],
11 [ 1.78816606, 0.12328895, 0.53822894, 1.58932956],
12 [ 0.55363975, 0.17329085, 0.03561944, -0.79536074]])
13 >>>
14 >>> names == 'bob' #数组的比较运算是矢量化的
15 array([ True, False, False, True, False, False, False])
16 >>> data = np.random.randn(7, 4)
17 >>> data[names == 'bob'] #布尔型数组用于数组索引
18 array([[ 0.90834313, -0.11373769, 0.13405157, 0.14890507],
19 [ 1.23918751, -0.25025211, -0.26848528, -0.19568496]])
20 >>> data
21 array([[ 0.90834313, -0.11373769, 0.13405157, 0.14890507],
22 [-1.43803588, 0.27400888, 0.95506627, -1.68159653],
23 [-1.11827716, -0.36084883, 1.59143787, 1.33349614],
24 [ 1.23918751, -0.25025211, -0.26848528, -0.19568496],
25 [-2.37793176, -0.11967421, -0.25341328, -0.15386212],
26 [-0.03628671, -1.3188123 , 0.17480482, -0.93195373],
27 [-0.55657692, -0.12547058, -0.31571666, 0.1365729 ]])
28 >>> data[names == 'bob', 2:] #可将布尔类型数组跟切片混合使用
29 array([[ 0.13405157, 0.14890507],
30 [-0.26848528, -0.19568496]])
31 >>> data[names == 'bob', 3]
32 array([ 0.14890507, -0.19568496])
33 >>> names != 'bob' #也可使用!=
34 array([False, True, True, False, True, True, True])
35 >>> data[~(names == 'bob')]
36 array([[-1.43803588, 0.27400888, 0.95506627, -1.68159653],
37 [-1.11827716, -0.36084883, 1.59143787, 1.33349614],
38 [-2.37793176, -0.11967421, -0.25341328, -0.15386212],
39 [-0.03628671, -1.3188123 , 0.17480482, -0.93195373],
40 [-0.55657692, -0.12547058, -0.31571666, 0.1365729 ]])
41 >>> mask = (names == 'bob') | (names == 'will')
42 >>> mask
43 array([ True, False, True, True, True, False, False])
44 >>> data[mask]
45 array([[ 0.90834313, -0.11373769, 0.13405157, 0.14890507],
46 [-1.11827716, -0.36084883, 1.59143787, 1.33349614],
47 [ 1.23918751, -0.25025211, -0.26848528, -0.19568496],
48 [-2.37793176, -0.11967421, -0.25341328, -0.15386212]])
49 >>> data[data < 0] = 0 #通过布尔值设置值
50 >>> data
51 array([[0.90834313, 0. , 0.13405157, 0.14890507],
52 [0. , 0.27400888, 0.95506627, 0. ],
53 [0. , 0. , 1.59143787, 1.33349614],
54 [1.23918751, 0. , 0. , 0. ],
55 [0. , 0. , 0. , 0. ],
56 [0. , 0. , 0.17480482, 0. ],
57 [0. , 0. , 0. , 0.1365729 ]])
58 >>> data[names != 'joe'] = 7
59 > >>> arr = np.empty((8, 4))
60 >>> for i in range(8): arr[i] = i
61 ...
62 >>> arr
63 array([[0., 0., 0., 0.],
64 [1., 1., 1., 1.],
65 [2., 2., 2., 2.],
66 [3., 3., 3., 3.],
67 [4., 4., 4., 4.],
68 [5., 5., 5., 5.],
69 [6., 6., 6., 6.],
70 [7., 7., 7., 7.]])
71 >>> arr[[4, 3, 0, 6]]
72 array([[4., 4., 4., 4.],
73 [3., 3., 3., 3.],
74 [0., 0., 0., 0.],
75 [6., 6., 6., 6.]])
76 >>> arr[[-3, -5, -7]]
77 array([[5., 5., 5., 5.],
78 [3., 3., 3., 3.],
79 [1., 1., 1., 1.]])>> data
80 array([[7. , 7. , 7. , 7. ],
81 [0. , 0.27400888, 0.95506627, 0. ],
82 [7. , 7. , 7. , 7. ],
83 [7. , 7. , 7. , 7. ],
84 [7. , 7. , 7. , 7. ],
85 [0. , 0. , 0.17480482, 0. ],
86 [0. , 0. , 0. , 0.1365729 ]])
87 >>>
1.7 花式索引
花式索引(Fancy indexing)是一个NumPy术语,它指的是利用整数数组进行索引。
1 >>> arr = np.empty((8, 4))
2 >>> for i in range(8): arr[i] = i
3 ...
4 >>> arr
5 array([[0., 0., 0., 0.],
6 [1., 1., 1., 1.],
7 [2., 2., 2., 2.],
8 [3., 3., 3., 3.],
9 [4., 4., 4., 4.],
10 [5., 5., 5., 5.],
11 [6., 6., 6., 6.],
12 [7., 7., 7., 7.]])
13 >>> arr[[4, 3, 0, 6]] #以特定顺序选取行子继,只需要传入一个用于指定顺序的整数列表或ndarray
14 array([[4., 4., 4., 4.],
15 [3., 3., 3., 3.],
16 [0., 0., 0., 0.],
17 [6., 6., 6., 6.]])
18 >>> arr[[-3, -5, -7]] #使用负数将从末尾开始选取行
19 array([[5., 5., 5., 5.],
20 [3., 3., 3., 3.],
21 [1., 1., 1., 1.]])
一次传入多个索引数组有有一点特别,它返回的是一个一维数组,其中的元素对应各个索引元组。
1 >>> arr = np.arange(32).reshape((8, 4))
2 >>> arr
3 array([[ 0, 1, 2, 3],
4 [ 4, 5, 6, 7],
5 [ 8, 9, 10, 11],
6 [12, 13, 14, 15],
7 [16, 17, 18, 19],
8 [20, 21, 22, 23],
9 [24, 25, 26, 27],
10 [28, 29, 30, 31]])
11 >>> arr[[1, 5, 7, 2], [0, 3, 1, 2]] #最终选取的元素是(1, 0) (5, 3) (7, 1) (2, 2)
12 array([ 4, 23, 29, 10])
上面的代码没有达到我们想要的效果,我们想要的是选取矩阵的行列子集应该是矩阵区域的形式才对。
1 >>> arr
2 array([[ 0, 1, 2, 3],
3 [ 4, 5, 6, 7],
4 [ 8, 9, 10, 11],
5 [12, 13, 14, 15],
6 [16, 17, 18, 19],
7 [20, 21, 22, 23],
8 [24, 25, 26, 27],
9 [28, 29, 30, 31]])
10 >>> arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]
11 array([[ 4, 7, 5, 6],
12 [20, 23, 21, 22],
13 [28, 31, 29, 30],
14 [ 8, 11, 9, 10]])
另一个方式是使用np.ix_函数,它可以将两个一维整型数组转换为一个用于选取方形区域的索引器。
1 >>> arr
2 array([[ 0, 1, 2, 3],
3 [ 4, 5, 6, 7],
4 [ 8, 9, 10, 11],
5 [12, 13, 14, 15],
6 [16, 17, 18, 19],
7 [20, 21, 22, 23],
8 [24, 25, 26, 27],
9 [28, 29, 30, 31]])
10 >>> arr[np.ix_([1, 5, 7, 2], [0, 3, 1, 2])]
11 array([[ 4, 7, 5, 6],
12 [20, 23, 21, 22],
13 [28, 31, 29, 30],
14 [ 8, 11, 9, 10]])
花式索引跟切片不一样,它总是将数据复制到新数组中。
1.8 数组转置与轴对称
转置(transpose)是重塑的一种特殊方式,它返回的是源数据的视图。数组还有一个特殊的T属性(类似于矩阵的转置)。

1 >>> arr = np.arange(15).reshape((3, 5))
2 >>> arr
3 array([[ 0, 1, 2, 3, 4],
4 [ 5, 6, 7, 8, 9],
5 [10, 11, 12, 13, 14]])
6 >>> arr.T
7 array([[ 0, 5, 10],
8 [ 1, 6, 11],
9 [ 2, 7, 12],
10 [ 3, 8, 13],
11 [ 4, 9, 14]])
np.dot可计算矩阵内积XTX。
1 >>> arr = np.array([[1, 2, 3], [4, 5, 6]])
2 >>> arr
3 array([[1, 2, 3],
4 [4, 5, 6]])
5 >>> np.dot(arr.T, arr)
6 array([[17, 22, 27],
7 [22, 29, 36],
8 [27, 36, 45]])
9 >>>

