20172327 2018-2019-1 《程序设计与数据结构》第八周学习总结
20172327 2018-2019-1 《程序设计与数据结构》第八周学习总结
教材学习内容总结
第十二章 优先队列与堆
| 堆 |
1.最小堆(minheap):对是一个完全二叉树,其中的每个结点都小于或等于它的两个孩子。
2.最大堆(maxheap):对是一个完全二叉树,其中的每个结点都大于或等于它的两个孩子。
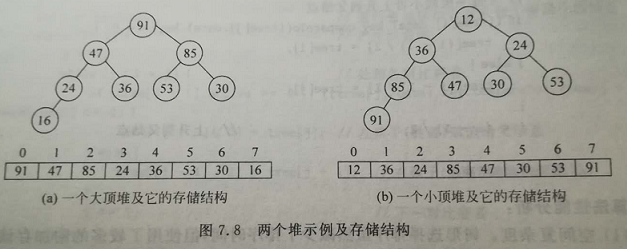
3.最小堆将其最小的元素储存在该二叉树的根处,且其根的两个孩子也同样是最小堆
4.addElement操作
将元素添加为新的叶结点,同时保持树是完全树,将该元素向根的地方移动,将它与父结点对换,直到其中的元素大小关系满足要求为止。
- 在链表实现中:在链表实现中,添加元素时首先要确定插入结点的双亲。最坏的一种情况是从右下的最后一个叶子节点一直遍历到根,在遍历到堆的左下结点 。该过程的时间复杂度为2logn。下一步是插入节点(简单的赋值,这里的时间复杂度为O(1))。最后一步是将这棵树进行重新排序。因为从根到结点的路径长度为logn,所以最多需要进行logn此操作。因此使用链表实现时操作的复杂度为2*logn+1+logn。即O(logn)
- 在链表实现中:在数组实现中,添加元素时并不需要确定新结点双亲的步骤,但是,其他两个步骤与链表实现的一样。因此,数组实现的addElement操作的时间复杂度为1+logn或O(logn)。虽然这两者实现的复杂度相同,但数组实现的效率更高一些。
5.removeMin操作
利用最后的叶结点来取代根,然后将其向下移动到合适的位置。
- 在链表实现中:removeMin必须删除根元素,并用最后一个结点的元素来替换它(简单的赋值,时间复杂度为O(1))。下面要对该树进行重新排序,因为该树原先是一个堆,所以只需要跟较小的一边进行比较排序。因为从根到叶子的最大路径长度为logn,因此该步骤的时间复杂度为O(logn)。到此时,这棵树已经完成了,但在实际进行的过程中,为了继续完成接下来的操作,我们还要找到新的最末结点,最坏的情况是进行丛叶子到根的遍历,然后再从根往下到另一叶子的遍历。因此,该步骤的时间复杂度为2logn。于是removeMin操作最后的时间复杂度为2logn+logn+1,即O(logn)。
- 在数组实现中:removeMin也像链表实现的那样,只不过它不需要确定最新的最末结点。因此,数组实现的removeMin操作的复杂度为logn+1。即O(logn)。
6.findMin操作
此操作较简单,因为在添加元素的过程中就已经把最小元素移动到了根位置。
7.堆和二叉排序树的区别:
- 1.堆是一棵完全二叉树,二叉排序树不一定是完全二叉树;
- 2.在二叉排序树中,某结点的右孩子结点的值一定大于该结点的左孩子结点的值,在堆中却不一定;
- 3.在二叉排序树中,最小值结点是最左下结点,最大值结点是最右下结点。在堆中却不一定。
| 堆的实现(以最大堆为例) |
1.最大堆接口的实现:
public interface MaxHeap<T extends Comparable<T>> extends BinaryTree<T>
{
// Adds the specified object to the heap.
public void add (T obj);
// Returns a reference to the element with the highest value in the heap.
public T getMax ();
// Removes and returns the element with the highest value in the heap.
public T removeMax ();
}
2.在 LinkedMaxHeap 中的 add 方法依赖于HeapNode中的两个方法:getParentAdd 和 heapifyAdd 方法。
其中 getParentAdd 方法从树的最后一个结点开始,一个一个检测,寻找新加入结点的父结点。从树中开始向上查找,直到发现它是某个结点的左子结点,或是到达根结点时为止。如果到达根结点,新的父结点是根的左后继结点。如果没有到达根结点,则再查找右子结点的最左后继。删除的成本。
public HeapNode<T> getParentAdd (HeapNode<T> last)
{
HeapNode<T> result = last;
while ((result.parent != null) && (result.parent.left != result))
result = result.parent;
if (result.parent != null)
if (result.parent.right == null)
result = result.parent;
else
{
result = (HeapNode<T>) result.parent.right;
while (result.left != null)
result = (HeapNode<T>) result.left;
}
else
while (result.left != null)
result = (HeapNode<T>) result.left;
return result;
}
一旦新的叶结点添加到树中,heapifyAdd 方法就利用 parent 引用沿树向上移动,必要时交换元素。(交换的是元素,不是结点)
public void heapifyAdd (HeapNode<T> last)
{
T temp;
HeapNode<T> current = last;
while ((current.parent != null) &&
((current.element).compareTo(current.parent.element) > 0))
{
temp = current.element;
current.element = current.parent.element;
current.parent.element = temp;
current = current.parent;
}
}
| 堆排序 |
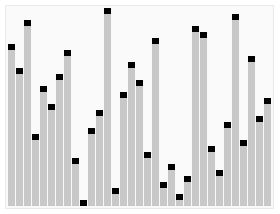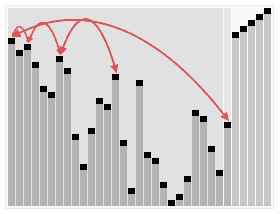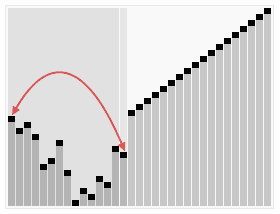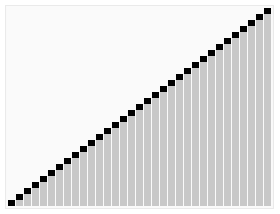
1.思路:将一组元素一项项地插入到堆中,然后一次删除一个。因为最大元素最先从堆中删除,所以一次次删除得到的元素将是有序序列,而且是降序的。同理,一个最小堆可用来得到升序的排序结果。
| 优先队列 |
1.两个规则:
1.具有更高优先级的项排在前.(不是FIFO)
2.具有相同优先级的项目按先进先出的规则排列。(FIFO)
2.实现方法:定义结点类保存队列中的元素、优先级和排列次序。然后,通过实现 Comparable 接口定义 compareTo 方法,先比较优先级,再比较排列次序。
教材学习中的问题和解决过程
- 问题1:对于堆排序的详细步骤(具体顺序)不清楚,教材上也只提供了思路。
- 解决方案:
【步骤一】构造初始堆,以大顶堆为例,给无序序列构造一个大顶堆,假设无序序列如下:
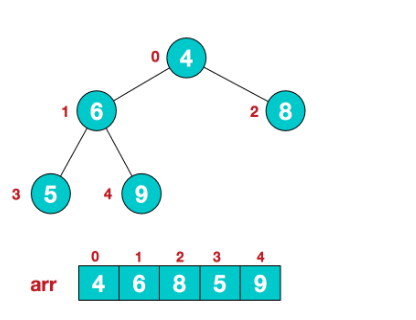
从最后一个非叶子结点开始(叶结点不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整:
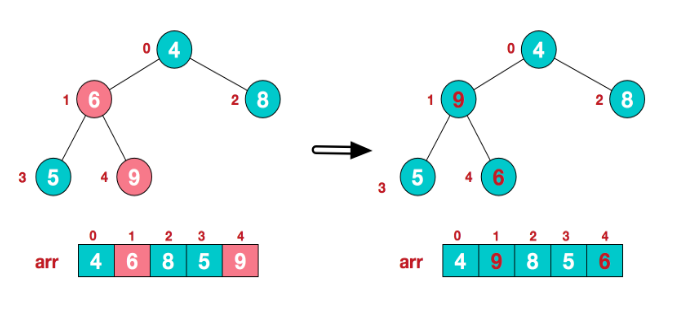
找到第二歌非页结点4,由于[4、9、8]中9最大,4和9交换/
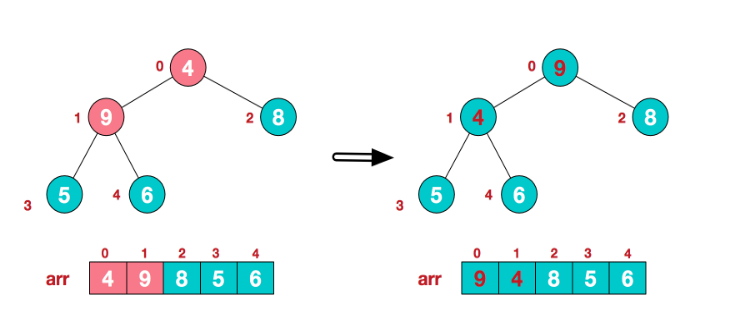
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
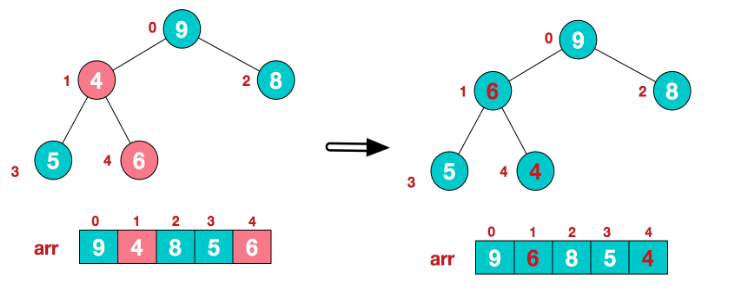
这样大顶堆就完成了。
【步骤二】将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。首先将堆顶元素9和末尾元素4进行交换:
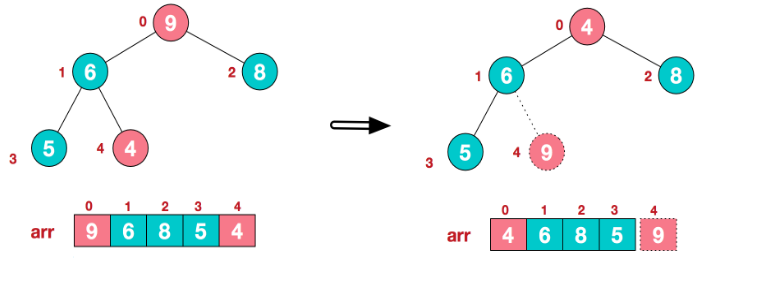
重新调整结构,使其继续满足堆定义:
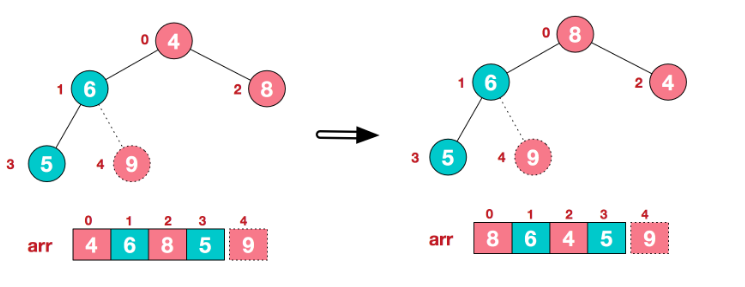
再将堆顶元素8与末尾元素5进行交换,得到第二大元素8:
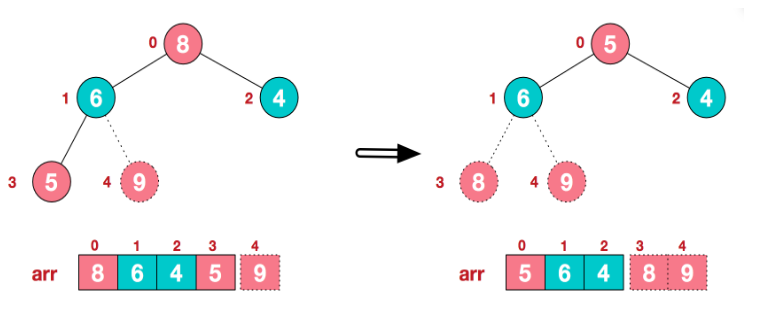
【步骤三】如此反复进行交换、重建、交换。反复进行此过程,便可得到有序序列:

所以,基本步骤概括为:将无序堆构建成大顶堆或小顶堆,再通过反复交换堆顶元素和当前末尾元素并调整,最后使整个序列有序。
代码调试中的问题和解决过程
暂无
上周考试错题总结
-
错题1.In removing an element from a binary search tree, another node must be ___________ to replace the node being removed.
A .duplicated
B .demoted
C .promoted
D .None of the above -
分析:在从二叉查找树中删除元素时, 另一个节点必须促进以替换要删除的节点。
-
错题2.The leftmost node in a binary search tree will contain the __________ element, while the rightmost node will contain the __________ element.
A .Maximum, minimum
B .Minimum, maximum
C .Minimum, middle
D .None of the above -
分析:二叉查找树中最左边的节点将包含最小元素, 而最右边的节点将包含最大元素。
-
错题3.One of the uses of trees is to provide _________ implementations of other collections.
A .efficient
B .easy
C .useful
D .None of the above -
分析:树的用途之一是提供其他集合的高效的实现。
-
错题4.The leftmost node in a binary search tree will contain the minimum element, while the rightmost node will contain the maximum element.
A .True
B .Flase -
分析:同错题2。
-
错题5.One of the uses of trees is to provide simpler implementations of other collections.
A .True
B .Flase -
分析:同错题3.
-
错题6.What type does "compareTo" return?
A .int
B .String
C .boolean
D .char -
分析:compareTo返回的是-1,0,1。所以为int值
-
错题7.Bubble, Selection and Insertion sort all have time complexity of O(n).
A .true
B .false -
分析:气泡和插入排序都具有 o (n) 的时间复杂度,但选择排序最好情况为O(n^2)。
-
错题8.Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
A .true
B .false -
分析:插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
代码托管
结对及互评
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, (加3分)
代码调试中的问题和解决过程, 无问题
感想,体会真切的(加1分)
点评认真,能指出博客和代码中的问题的(加1分)
-
20172317
基于评分标准,我给以上博客打分:4分。得分情况如下: -
20172320
基于评分标准,我给以上博客打分:8分。得分情况如下:- 结对学习内容
- 教材第12章,运行教材上的代码
- 完成课后自测题,并参考答案学习
- 完成程序设计项目:至少完成PP12.1、PP12.8、PP12.9
- 结对学习内容
其他(感悟、思考等,可选)
堆基于以前的所实现的,代码需要补充的不多,所以还好学。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 8/8 | |
| 第二周 | 1306/1306 | 1/2 | 20/28 | |
| 第三周 | 1291/2597 | 1/3 | 18/46 | |
| 第四周 | 4361/6958 | 2/3 | 20/66 | |
| 第五周 | 1755/8713 | 1/6 | 20/86 | |
| 第六周 | 3349/12062 | 1/7 | 20/106 | |
| 第七周 | 3308/15370 | 1/8 | 20/126 | |
| 第八周 | 4206/19576 | 2/10 | 20/146 |
-
计划学习时间:10小时
-
实际学习时间:8小时
-
改进情况:
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)


