20172327 2018-2019-1 《程序设计与数据结构》第六周学习总结
20172327 2018-2019-1 《程序设计与数据结构》第六周学习总结
教材学习内容总结
第十章 树
| 概述 |
1.树是一种非线性结构,其元素被组织成一个层次结构。
2.树由一个包含结点和边的集构成,元素被储存在结点中,边将一个结点和另一个结点连接起来。
3.每个结点都在一个特定层,根是位于该树顶层的唯一结点。
4.树中较低层的结点是上层结点的孩子,由同一个上层结点产生的多个结点互相称为兄弟,没有任何孩子的结点被称为叶子,至少有一个孩子的结点被称为内部结点。
5.通过计算根到结点所必须经过的边数目,就可以确定其路径长度。
6.树的高度是指从根到叶子最远的路径长度。
7.树中任一结点可以具有的最大孩子数目被称为度,孩子数目无限制的树称为广义树,每个结点限制不超过n个孩子的树称为n元树。
8.结点具有两个孩子的树称为二叉树。
9.平衡树:叶子都位于同一层或相差不超过一层的树称为平衡树。
10.M个元素的n元树具有的高度为lognM,一棵含有个结点的平衡二叉树具有的高度为log2N。
11.完全树:底层所有的叶子都靠左边排列的平衡树。
满树:叶子都位于同一层,且每一个结点要么是叶子,要么是正好具有n个孩子。
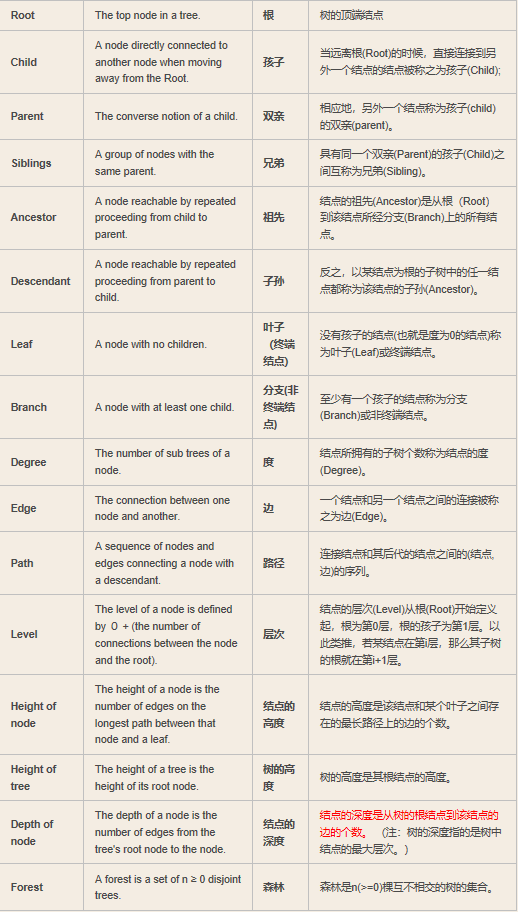
12.树的基本术语:
| 实现树的策略 |
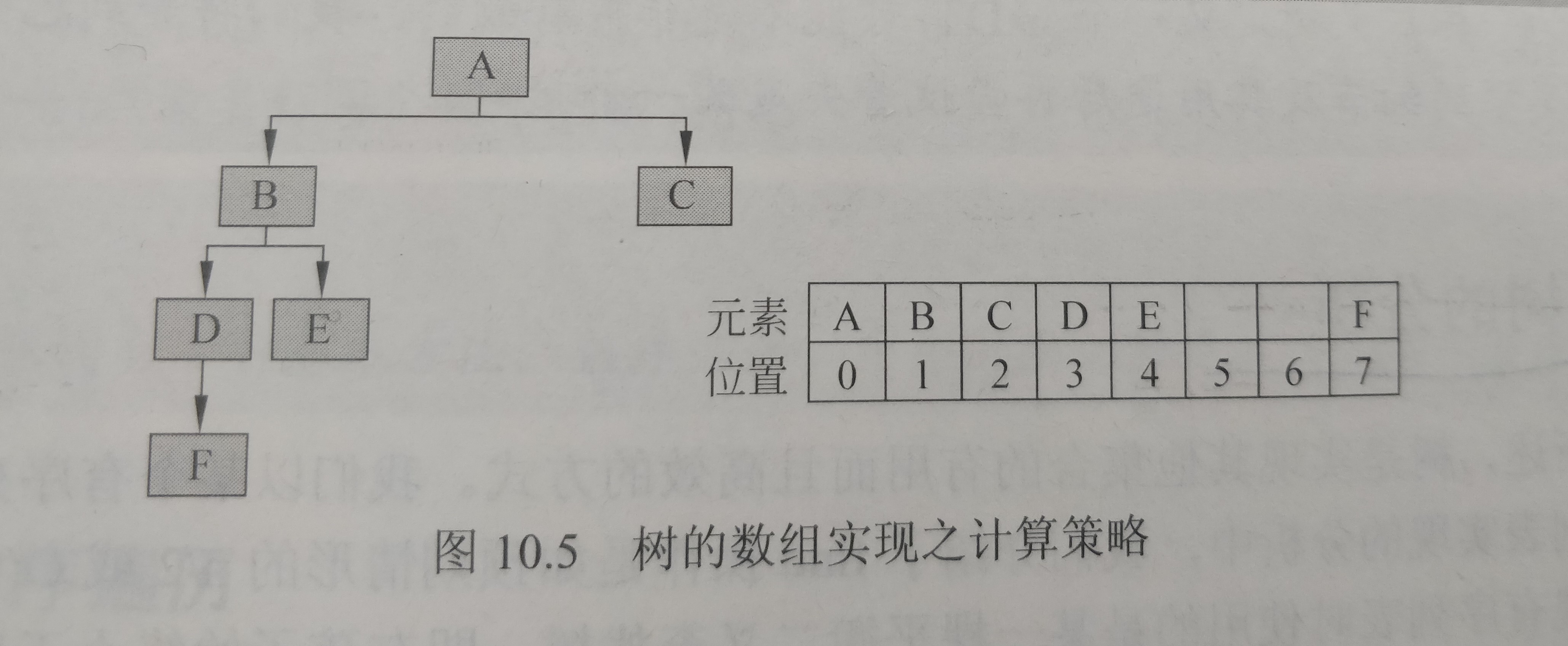
1.树的数组实现之计算策略:
对于任何储存在数组位置n处的元素而言,左孩子放在2n+1处,右孩子放在2(n+1)处.
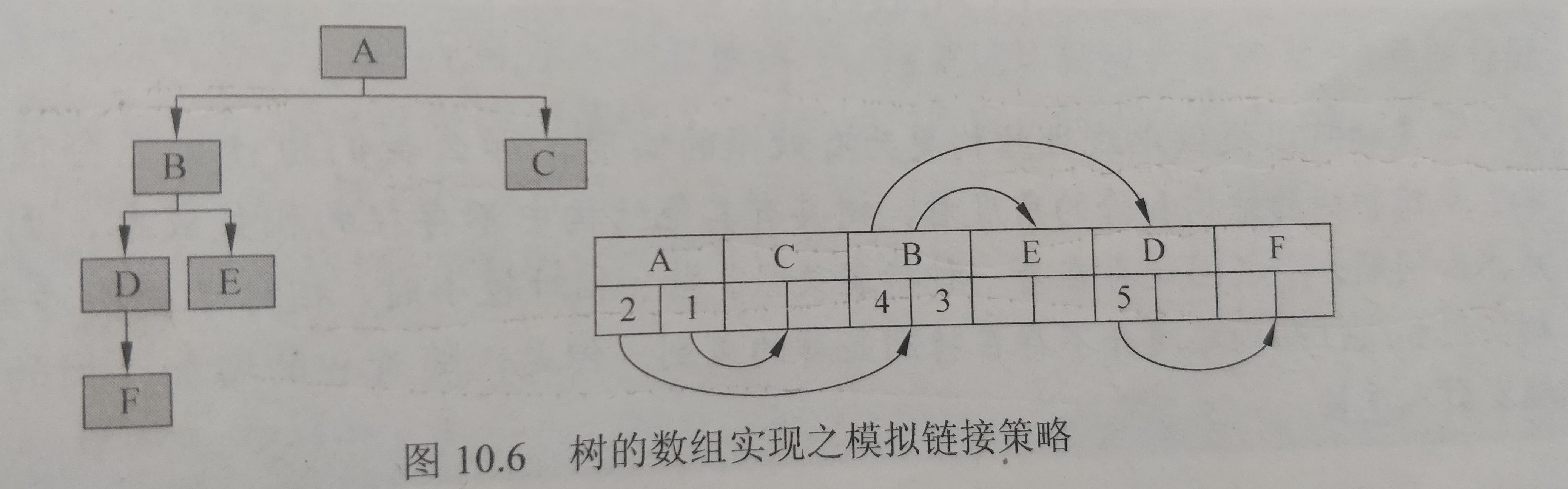
2.树的数组实现之模拟链接策略:
按照先来先服务的基准连续分配数组位置,每一个结点存储的是每一个孩子(可能还有双亲)的数组索引。不过这种方式增加了删除的成本。
3.树的分析:
在n相对较小时,相对于树所涉及的成本,树实现和线性结构之间并不存在特别显著的差别,但是,随着n的增加,树的效率就会越发引人注意。
| 树的遍历 |
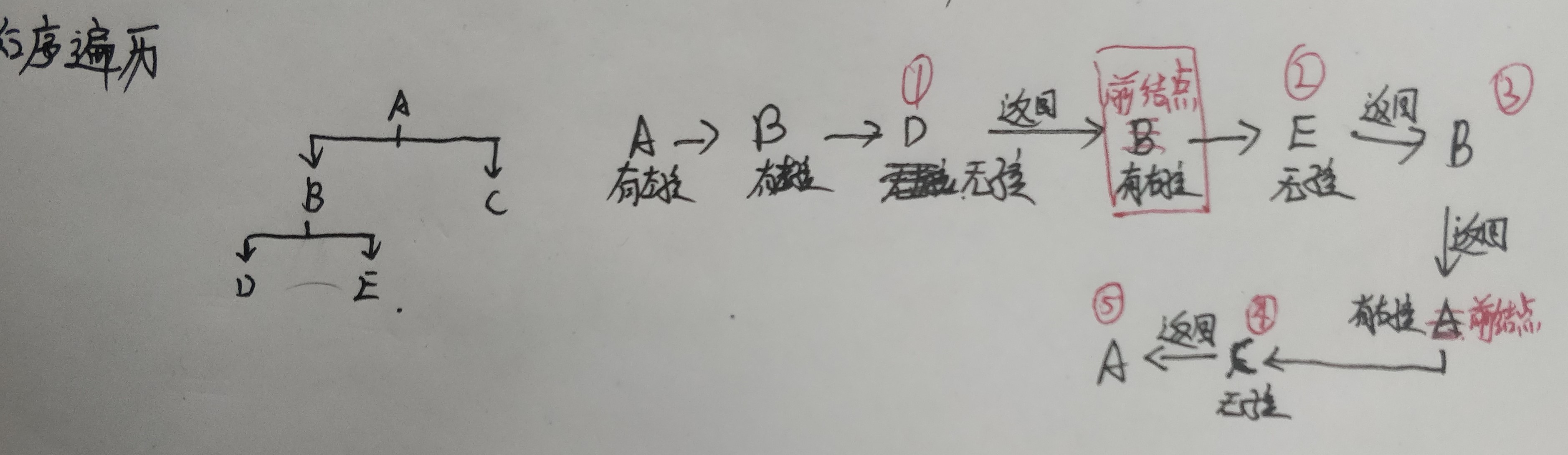
1.前序遍历:从根结点开始,访问每个子结点及其孩子。
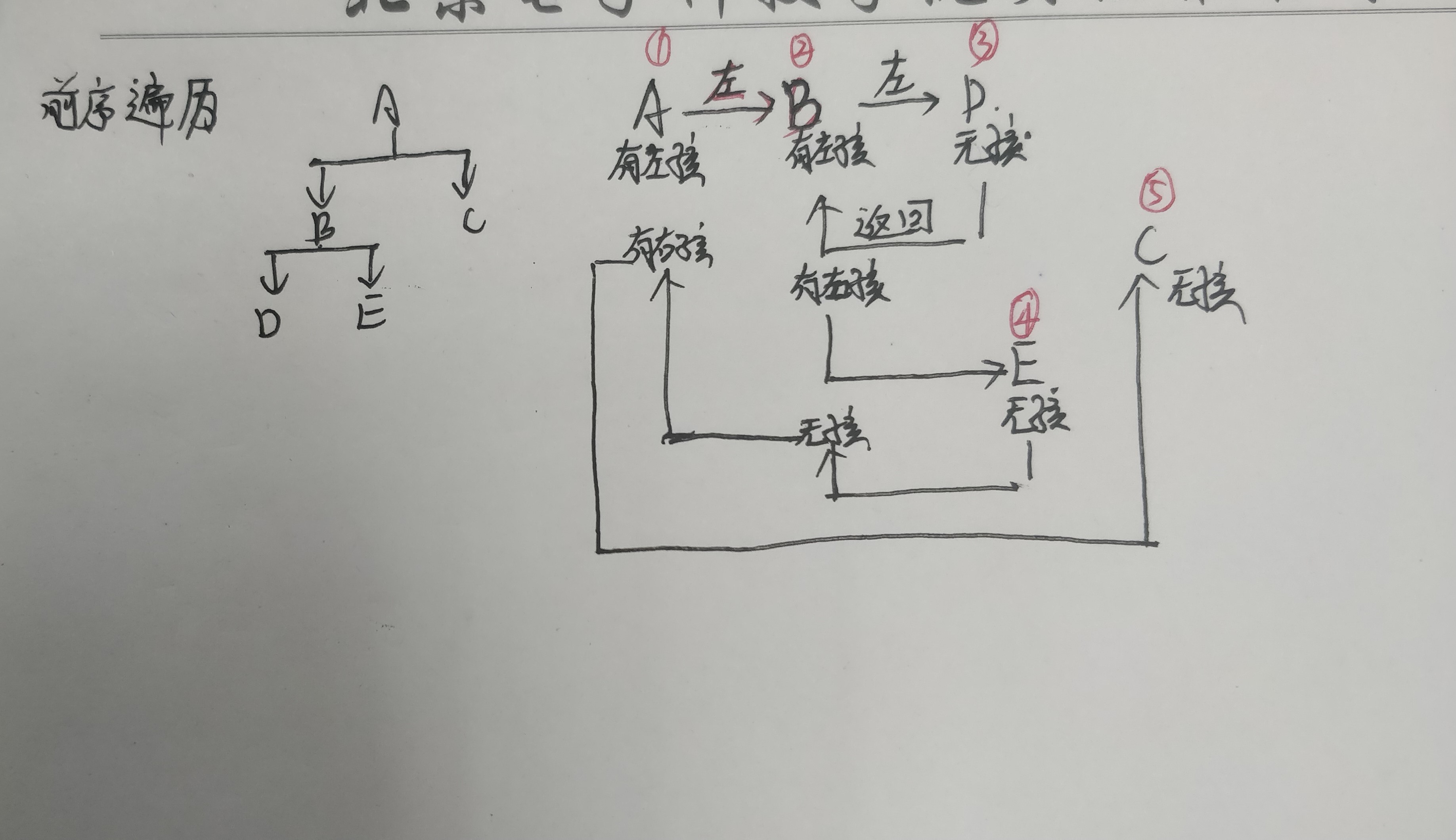
2.中序遍历:从根结点开始,访问结点的左孩子,然后时该结点,再然后时任何剩余结点。
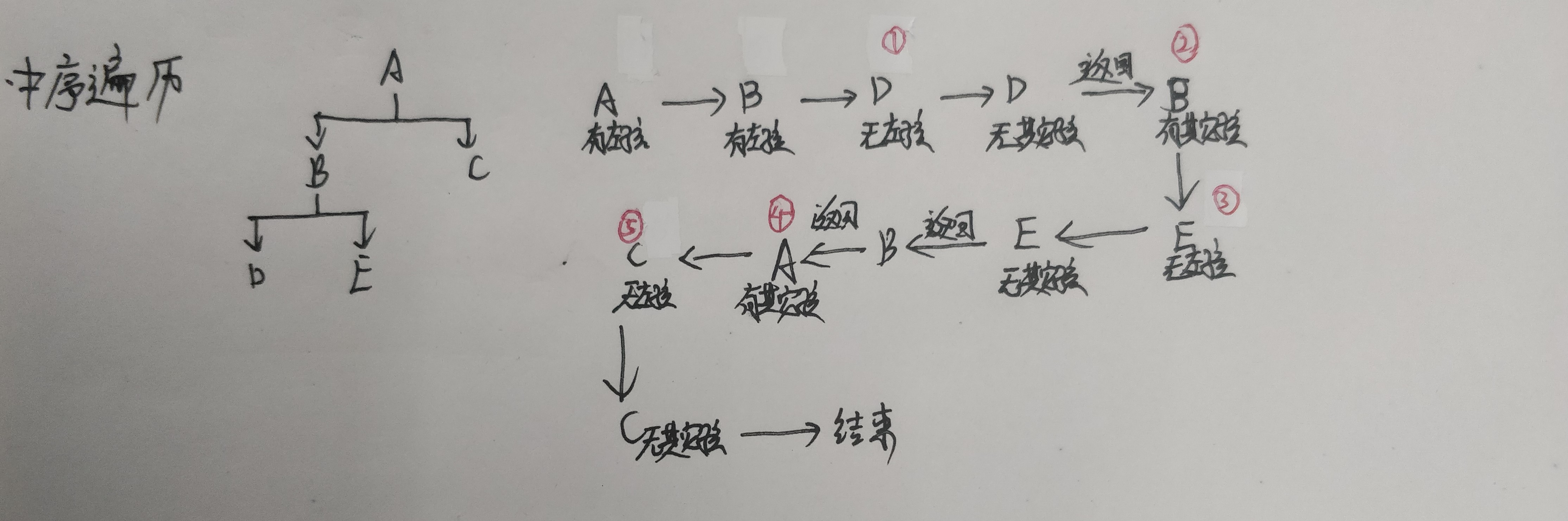
3.后序遍历:从根结点开始,访问结点的孩子,然后是该结点。
4.层序遍历:从根结点开始,访问每一层的所有结点,一次一层。

5.二叉树的遍历:二叉树的遍历是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。二叉树的遍历方式有很多,主要有前序遍历,中序遍历,后序遍历。
-
前序遍历
前序遍历的规则是:若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树

-
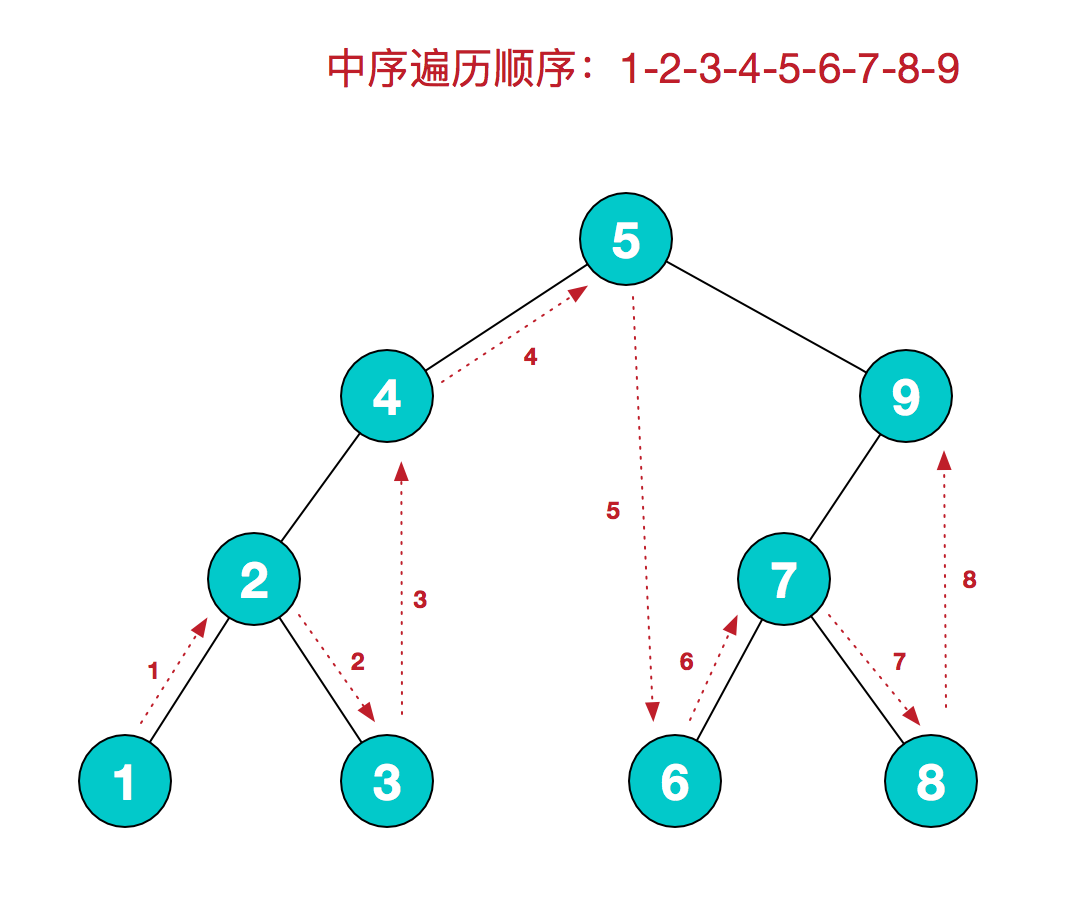
中序遍历
中序遍历的规则是:若树为空,则空操作返回;否则从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树。可以看到,如果是二叉排序树,中序遍历的结果就是个有序序列。
-
后序遍历
后序遍历的规则是:若树为空,则空操作返回;然后先遍历左子树,再遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。

| 二叉树 |
1.二叉树是树的特殊一种,具有如下特点:1、每个结点最多有两颗子树,结点的度最大为2。2、左子树和右子树是有顺序的,次序不能颠倒。3、即使某结点只有一个子树,也要区分左右子树。
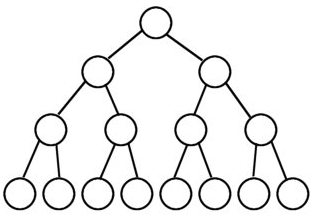
2.满二叉树(完美二叉树Perfect Binary Tree)
A Perfect Binary Tree(PBT) is a tree with all leaf nodes at the same depth.
All internal nodes have degree 2.
一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树。
3.完全二叉树(Complete Binary Tree)
A Complete Binary Tree (CBT) is a binary tree in which every level,
except possibly the last, is completely filled, and all nodes
are as far left as possible.
完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。
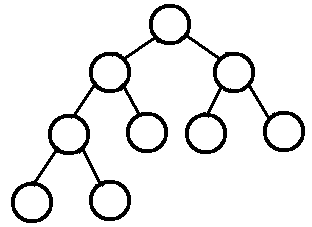
4.完满二叉树(Full Binary Tree)
A Full Binary Tree (FBT) is a tree in which every node other than the leaves has two children.
换句话说,所有非叶子结点的度都是2。(只要你有孩子,你就必然是有两个孩子。)
注:Full Binary Tree又叫做Strictly Binary Tree。

教材学习中的问题和解决过程
- 问题1:树的完全性是什么?
- 解决方案:完全树从根结点到倒数第二层满足满树,最后一层可以不完全填充,其叶子结点都靠左对齐。满树一定是一棵完全树。
- 问题2:树的度,节点的度,树的高度,深度以及节点的层次有什么区别?
- 解决方案:
1.节点的度分为0,1,2.及表示节点所含的分支个数。
2.树的度分为0,1,2即表示一棵树中最大节点的度,即哪个节点的子节点最多,它的度就是树的度。
3.树的高度,即从叶子节点开始,自底向上增加。
4.树的深度与树的高度相反,从根节点向下增加。
代码调试中的问题和解决过程
- 问题1:在实现ArrayOrderedListTest测试时,我遇到了显示最后一个数字时,人家显示为null这个问题。
图片 - 解决分析,在我对前面ArrayList类检查时,发现我在显示last时,将rear-1不小心写成rear了,所以它所读取的是最后一个后边的,所以肯定为空。
代码托管
结对及互评
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, (加3分)
代码调试中的问题和解决过程, 无问题
感想,体会真切的(加1分)
点评认真,能指出博客和代码中的问题的(加1分)
-
20172317
基于评分标准,我给以上博客打分:4分。得分情况如下: -
20172320
基于评分标准,我给以上博客打分:8分。得分情况如下:- 结对学习内容
- 教材第10章,运行教材上的代码
- 完成课后自测题,并参考答案学习
- 完成程序设计项目:至少完成PP10.1、PP10.3、PP10.5
- 结对学习内容
其他(感悟、思考等,可选)
这周学的有点麻烦,栈还行,就是链表有点糊涂。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 8/8 | |
| 第二周 | 1306/1306 | 1/2 | 20/28 | |
| 第三周 | 1291/2597 | 1/3 | 18/46 | |
| 第四周 | 4361/6958 | 2/3 | 20/66 | |
| 第五周 | 1755/8713 | 1/6 | 20/86 | |
| 第六周 | 3349/12062 | 1/7 | 20/106 |
-
计划学习时间:10小时
-
实际学习时间:8小时
-
改进情况:
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号